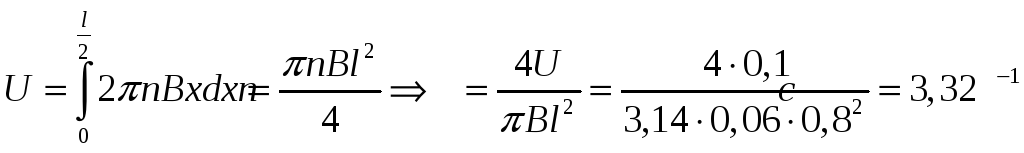Физика ИГЭУ Вар 10

Вариант 10

ИГЭУ, Иваново

Физика

Задача 1.1

Три точечных заряда 1нКл каждый расположены в вершинах равностороннего треугольника. Какой заряд нужно поместить в центре треугольника, чтобы вся система зарядов находилась в равновесии?

Д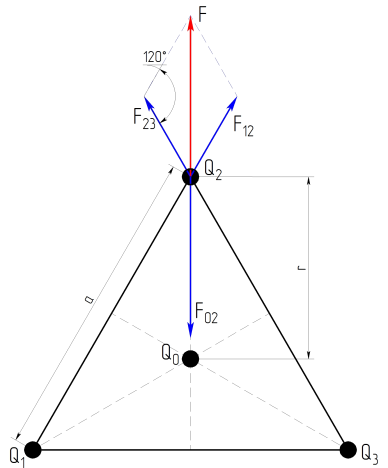ано:

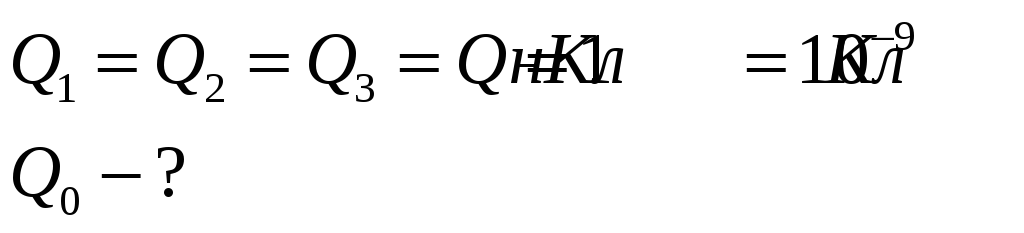
Рассмотрим силы действующие на заряд 2

По принципу суперпозиции

По закону Кулона

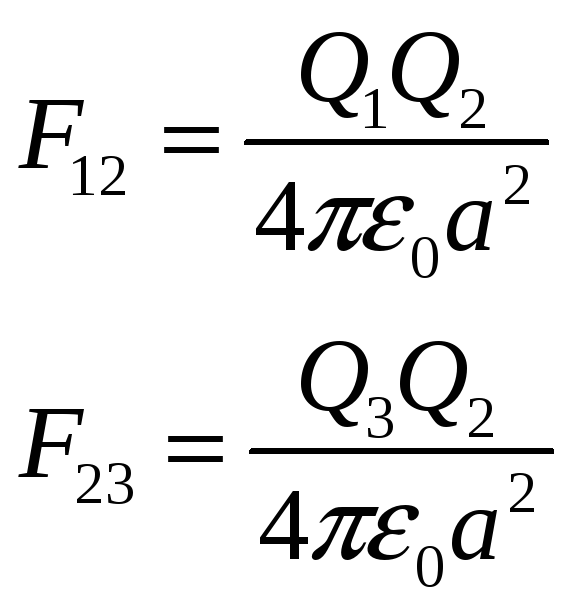
Центр треугольника пересечение его медиан. Известно, что точка пересечения медиан делит их в соотношении 2:1 считая от вершины треугольника

Расстояние до центра треугольника по теореме Пифагора

Складываем векторно силы и , по тереме косинусов

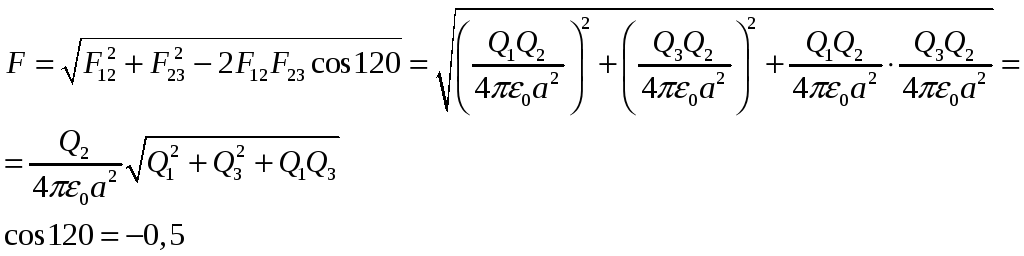
Складываем векторно силы и

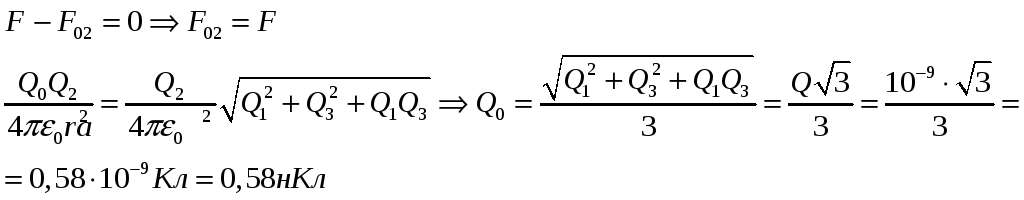
С учетом знака

Задача 1.28

По объёму парафинового шара радиусом 5см равномерно распределён заряд 2,78пКл (пикокулон). Определить напряжённость электрического поля внутри шара на расстоянии 1см от его центра. Диэлектрическая проницаемость парафина равна 2

Дано:

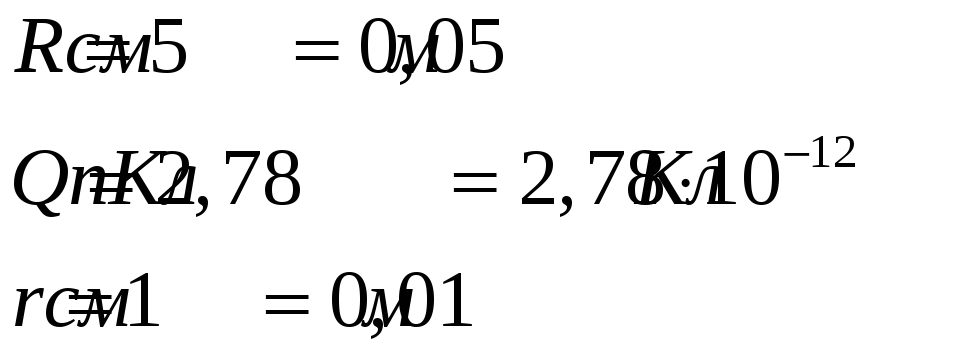
Объемная плотность заряда шара

По теореме Остроградского-Гаусса

Площадь поверхности мнимого шара

Заряд, находящийся внутри мнимого шара

Напряженность шара

Задача 2.1

Уединенному проводящему шару диаметром 30см сообщили заряд 9×10^-8Кл. Каким стал потенциал шара? Определить потенциал в центре шара и на расстоянии 15см от его поверхности в воздухе.

Дано:

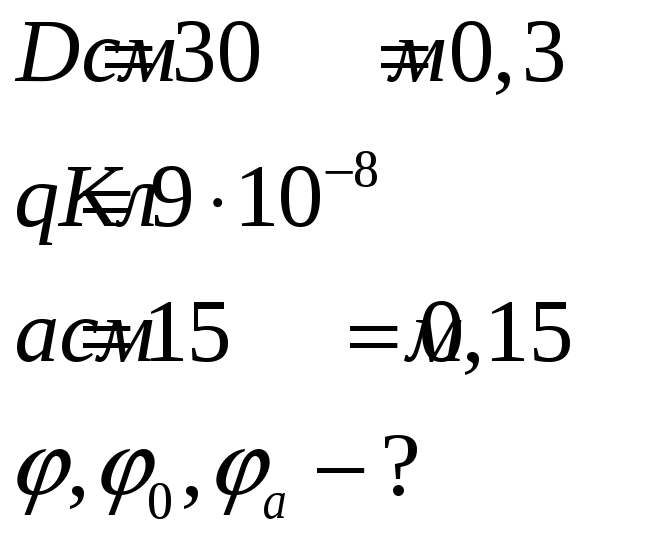
Потенциал шара

Емкость шара

Подставим (2) в (1), получим:

При

При

При

Задача 2.26

Капля масла диаметром 0,01мм удерживается между горизонтальными пластинами, расстояние между которыми равно 25мм. Какой заряд находится на капле, если разность потенциалов между пластинами равна 3,6×10⁴В? Плотность масла 900кг/м³.

Дано:

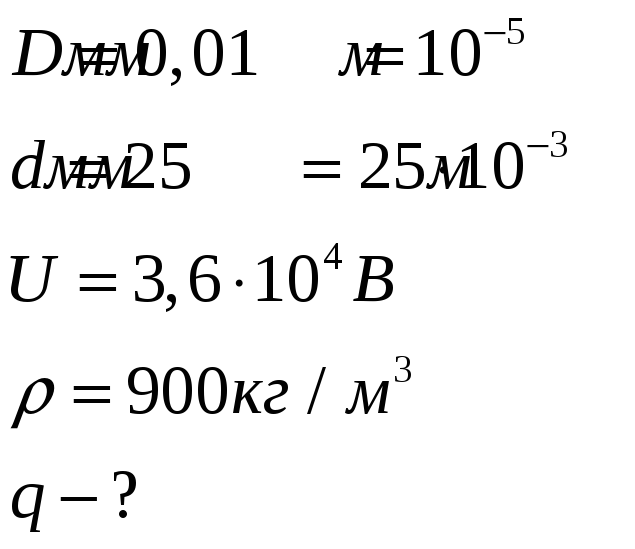
На каплю в электрическом поле действует сила Кулона и сила тяжести

Сила Кулона

По второму закону Ньютона

Напряженность электрического поля

Масса капли

Подставим (2) и (3) в (1), получим:

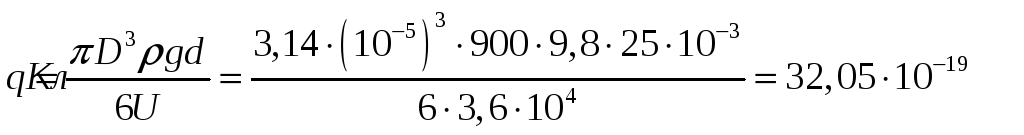
Задача 3.1

Расстояние между пластинами плоского конденсатора равно 1,2мм, площадь пластин – 40см². В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слой парафина толщиной 0,8мм и слой стекла толщиной 0,2мм. Какой заряд находится на конденсаторе, если разность потенциалов между его пластинами равна100В?

Дано:

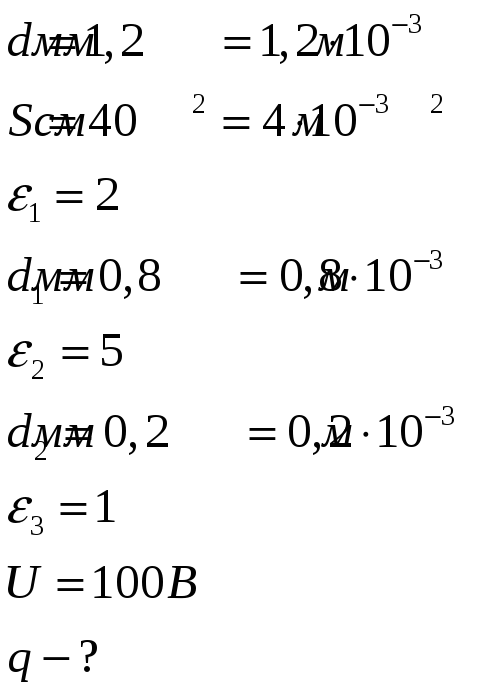
По определению электроемкость

Слои между обкладками конденсатора образуют три последовательно соединенных конденсатора

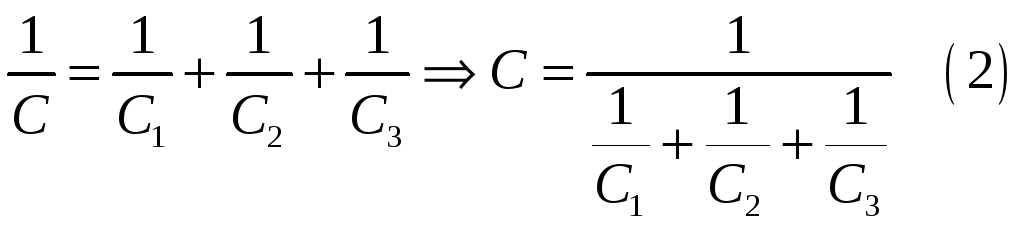
Электроемкость плоского конденсатора

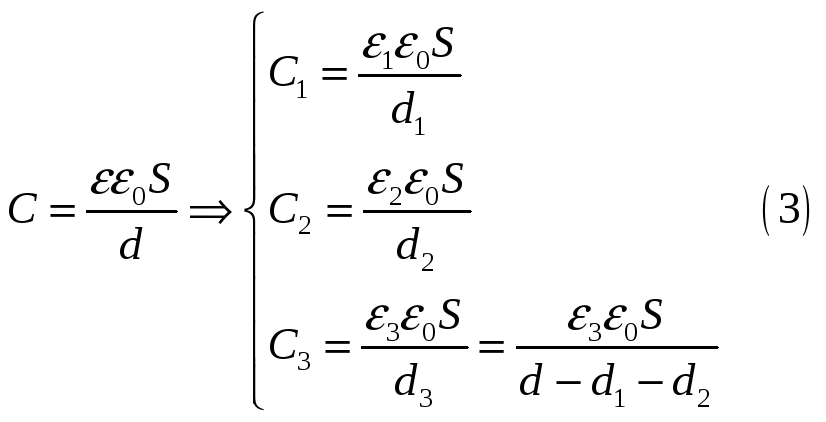
Подставим (2) с учетом (3) в (1), получим:

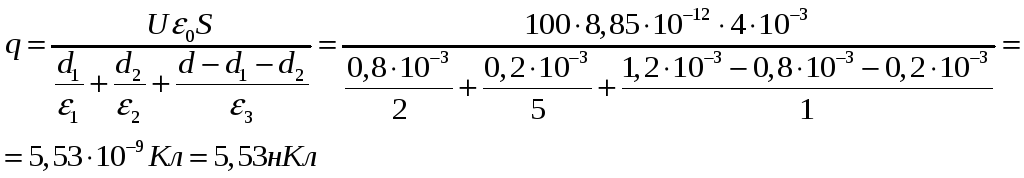
Задача 3.26

Определить энергию поля уединённой металлической сферы радиусом 0,2м, имеющей заряд 2мкКл.

Дано:

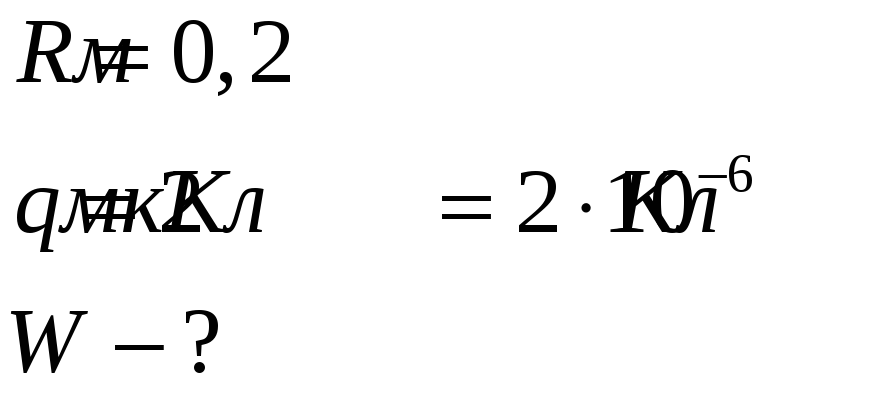
Энергия электрического поля

Емкость шара

Подставим (2) в (1), получим:

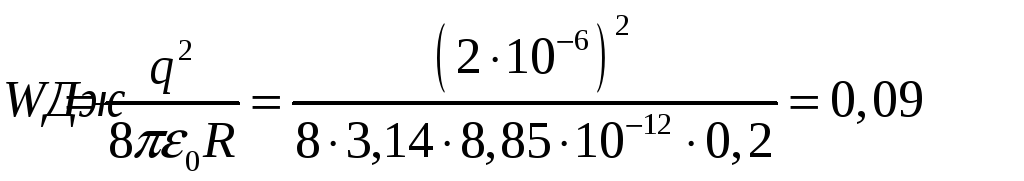
Задача 4.1

Определить число электронов, проходящих в секунду через единицу площади поперечного сечения медной проволоки длиной 20м и при напряжении на ее концах 16В. Удельное сопротивление меди 1,7×10^-8 Ом×м.

Дано:

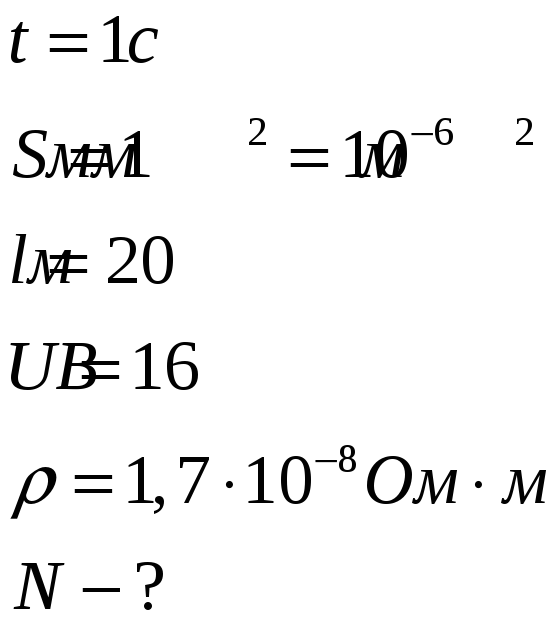
По закону Ома

С другой стороны сила тока

Сопротивление провода

Приравняем (1) и (2) с учетом (3), получим:

Задача 4.26

К зажимам источника тока присоединен нагреватель. ЭДС источника равна 24В, внутреннее сопротивление 1Ом. Нагреватель, включённый в цепь, потребляет мощность 80Вт. Определить силу тока в цепи и коэффициент полезного действия нагревателя.

Дано:

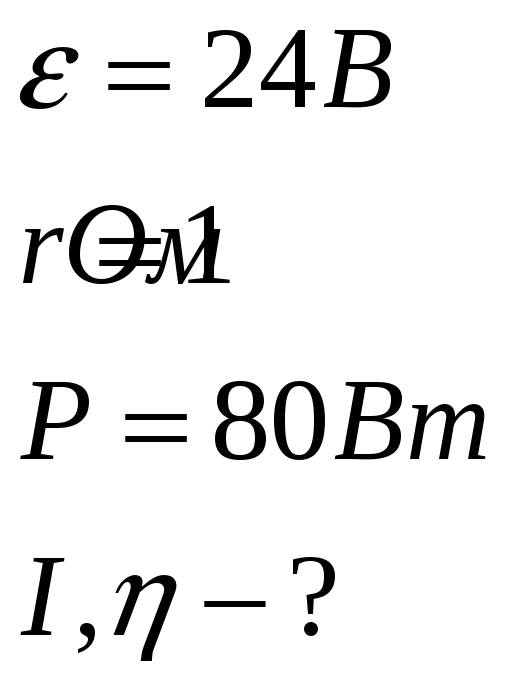
По закону Ома для полной цепи

Мощность, потребляемая внешней цепью

Подставим (2) в (1), получим:

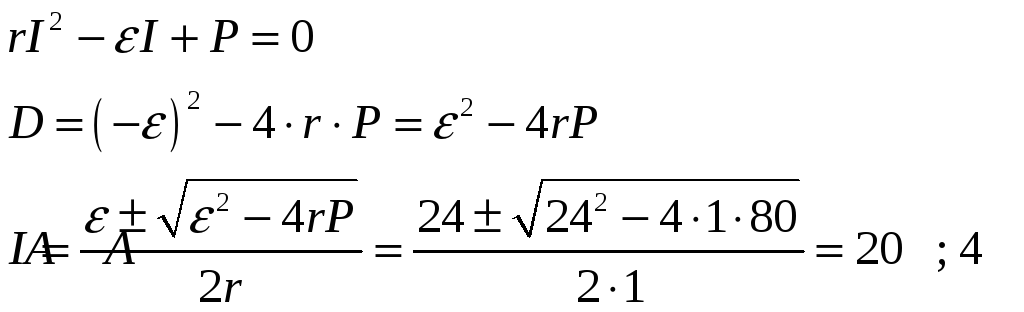
КПД нагревателя

При I=20A

При I=4A

Файл физика 2

Задача 1.1

Заряженная частица пролетает область однородного электричес­кого поля протяженностью d за время t. Скорость частицы на входе нап­равлена вдоль силовых линий поля и равна V. Масса частицы m, заряд q. Определить напряженность электрического поля.

Дано:

На частицу в электрическом поле действует кулоновская сила и по второму закону Ньютона

При равнопеременном движении

Подставим (2) в (1), получим:

Задача 1.26

Протон и α-частица, пройдя одинаковую ускоряющую разность потенциалов, влетают в однородное магнитное поле. Векторы их скоростей перпендикулярны силовым линиям поля. Найти отношение радиусов траекторий этих частиц.

Дано:

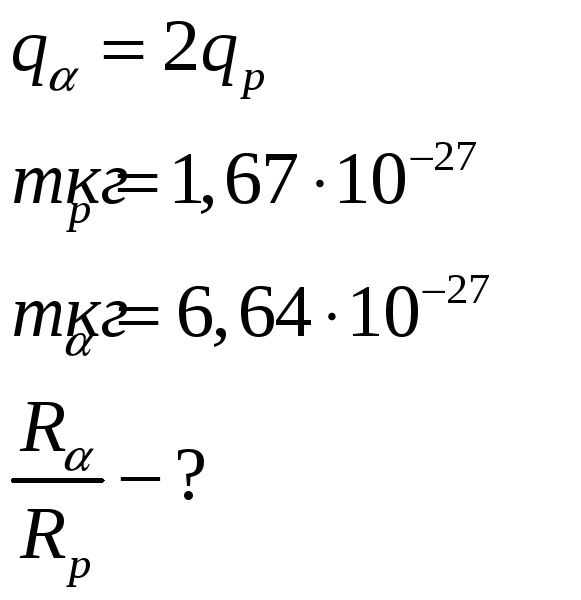
При движении заряженной частицы в магнитном поле по окружности (т.к. частицы влетели в поле под прямым углом), то на них действует сила Лоренца и центростремительная сила

По закону сохранения энергии

Подставим (2) в (1), получим:

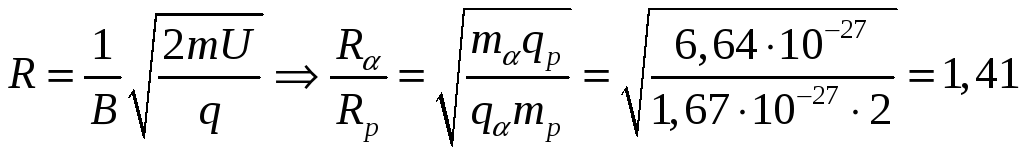
Задача 2.1

В магнитном поле на двух тонких проводниках горизонтально подвешен проводящий стержень, масса которого 20г, а длина 0,5м. Силовые линии магнитного поля направлены горизонтально и перпендикулярны к стержню. Найти индукцию магнитного поля, если при прохождении через стержень тока 5А сила натяжения проводников увеличилась в два раза.

Дано:

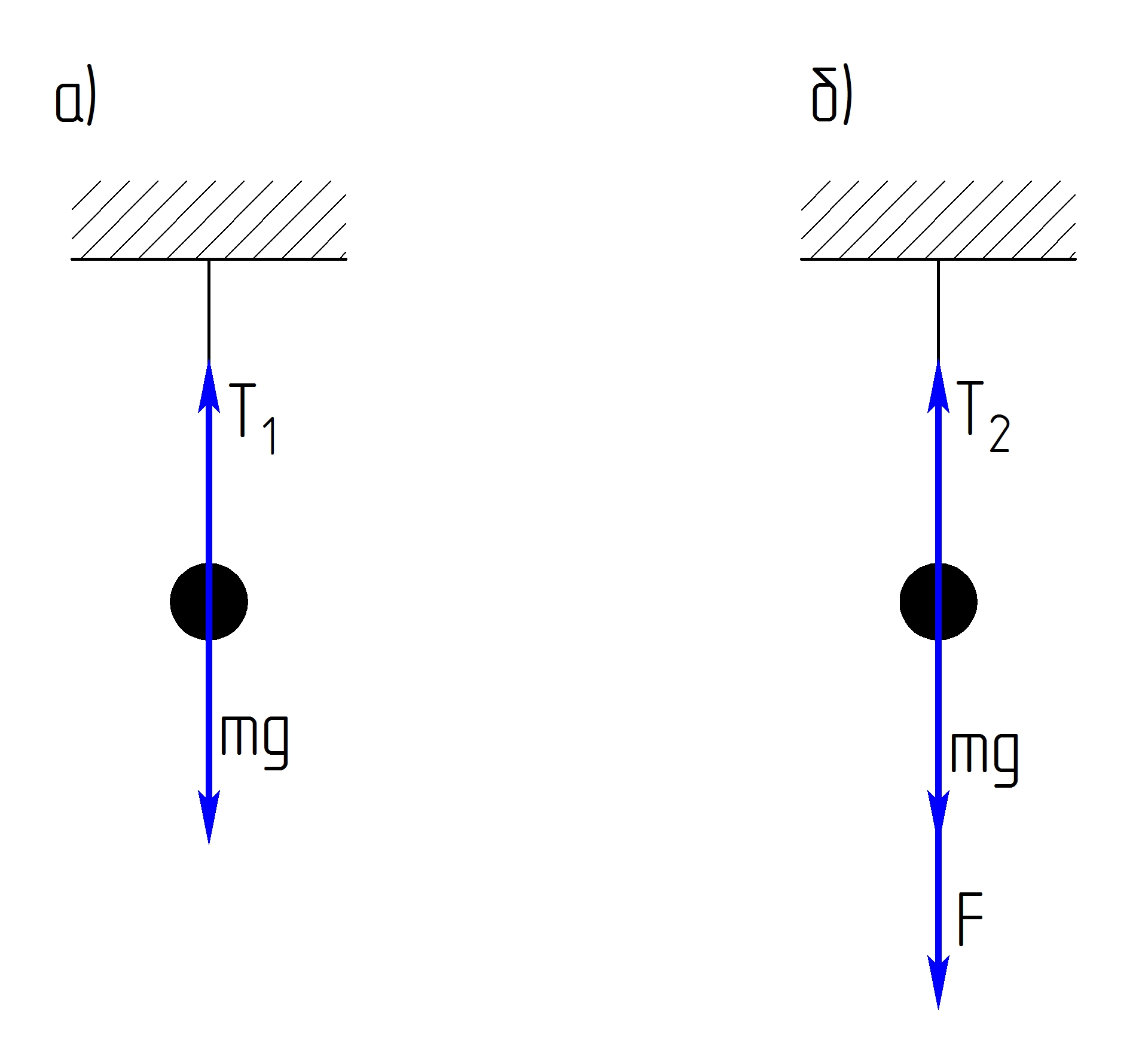
По второму закону Ньютона

• Для схемы а

• Для схемы б

Сила Ампера

По условию , тогда:

Задача 2.26

По длинному прямому проводнику течет ток I₁. Рядом с этим проводником расположена прямоугольная рамка со сторонами b и a, обтекаемая током I₂. Ближайшая сторона рамки находится на расстоянии l от проводника (рис. 2.8). Определить силу, действующую на рамку со стороны магнитного поля проводника.

Дано:

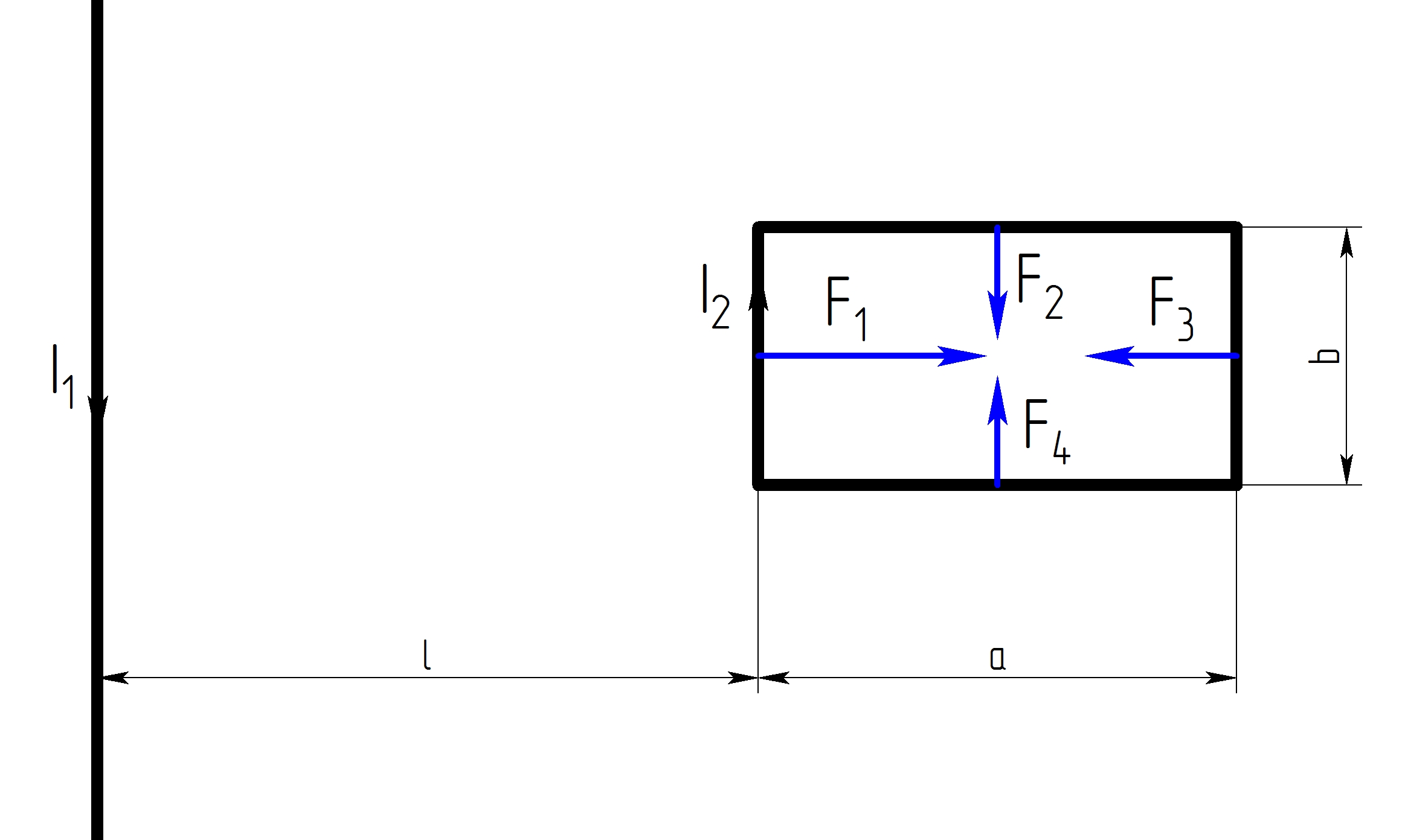
По принципу суперпозиции

Сила взаимодействия двух проводов с током

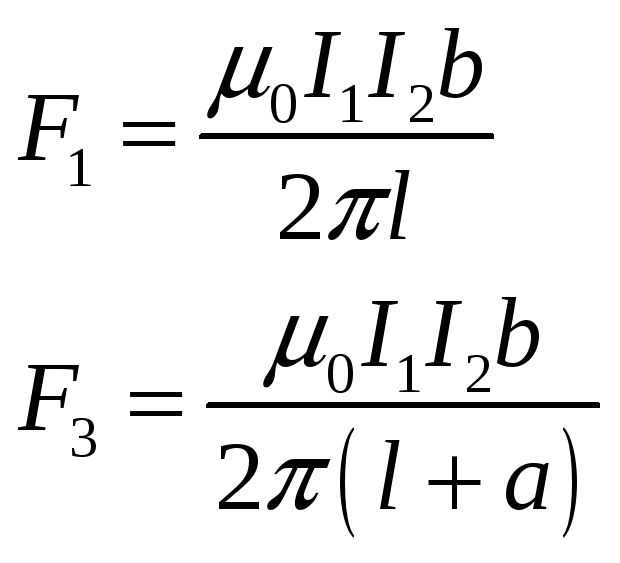
Тогда:

Задача 3.1

Определить индукцию магнитного поля в центре соленоида, со­держащего 500 витков, если сила тока в обмотке соленоида равна 10А. Длина соленоида равна 20см, его диаметр - 4см. Формулу магнитной индукции бесконечного соленоида считать неприменимой.

Дано:

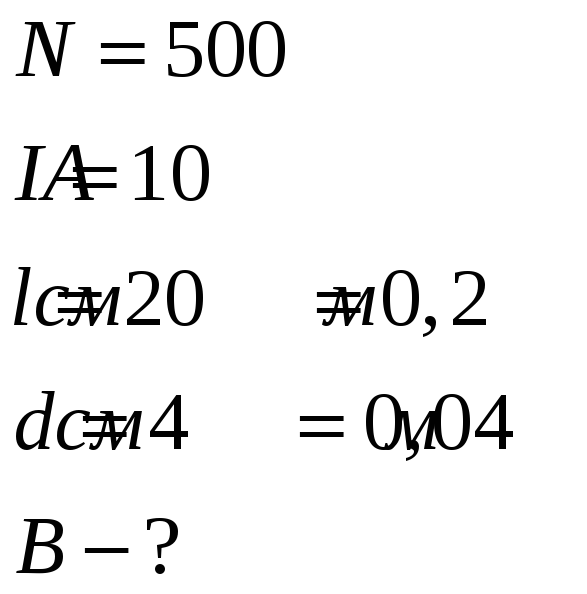
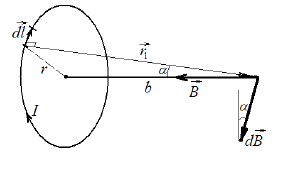
Магнитная индукция поля кругового тока на его оси

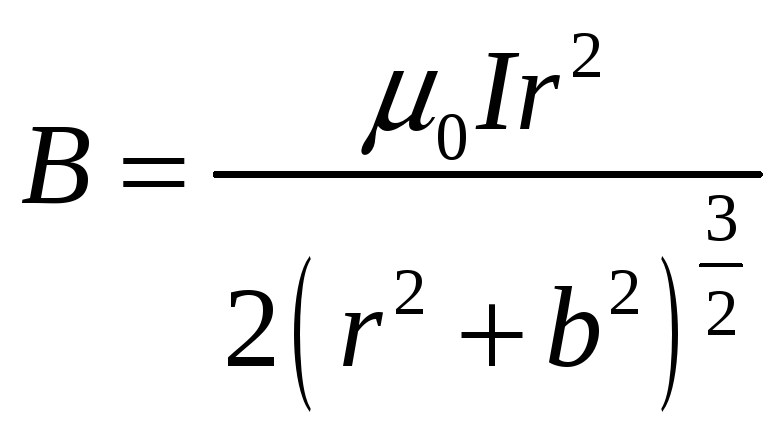
Для элемента длины dx соленоида, на котором находится витков. Данный элемент расположен на расстоянии x от центра соленоида точки С

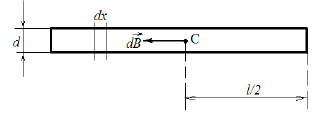
Тогда

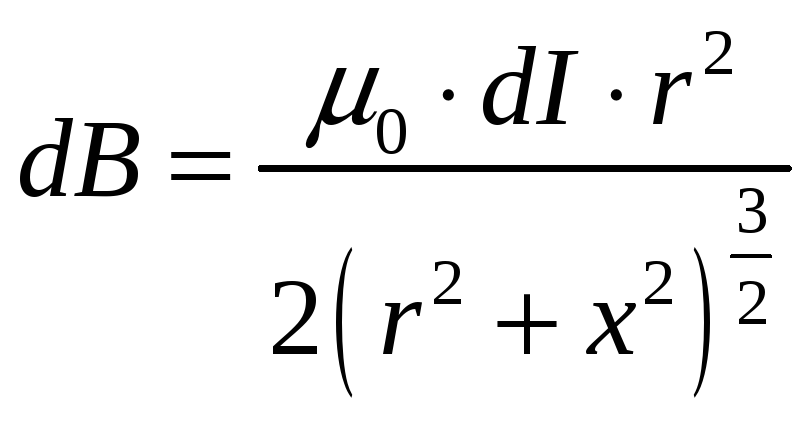
Ток, протекающий в элементе dx

Радиус соленоида

С учетом принципа суперпозиции

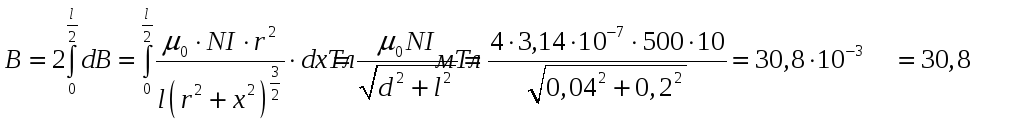
Задача 3.26

Пользуясь теоремой о циркуляции вектора индукции магнитного поля, вычислить расстояние, на котором бесконечный прямолинейный ток 10А создает магнитное поле индукцией 0,1мкТл.

Дано:

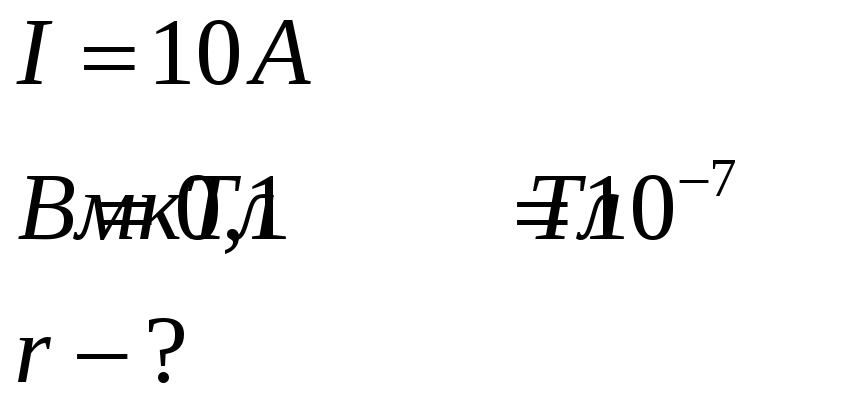
Применим теорему о циркуляции вектора индукции

Задача 4.1

В однородном магнитном поле с индукцией 0,1Тл вращается с постоянной частотой 5об/с стержень длиной 0,4м. Ось вращения перпен­дикулярна стержню и проходит через его конец, линии индукции поля направлены вдоль оси вращения. Найти разность потенциалов, возни­кающую на концах стержня.

Дано:

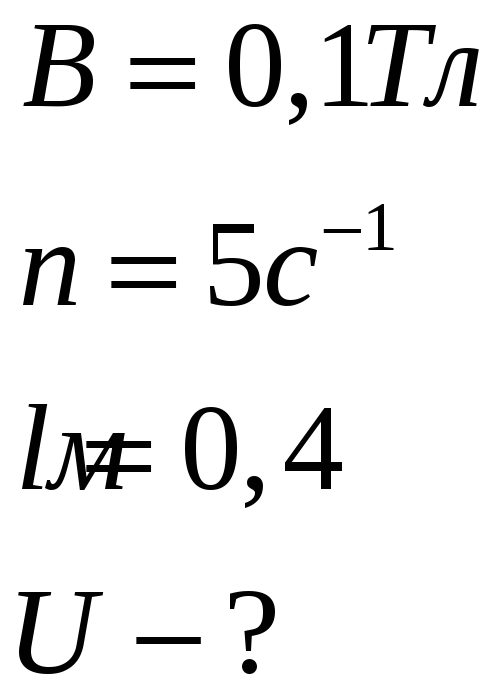
На электроны находящиеся в стержне действуют сила Лоренца и электрическая сила

Скорость электронов на расстоянии от оси вращения

Подставим (2) в (1):

Разность потенциалов

Задача 4.23

В однородном магнитном поле с индукцией 0,06Тл равномерно вращается вокруг вертикальной оси горизонтальный стержень длиной 0,8м. Ось вращения проходит через конец стержня и параллельна линиям индукции магнитного поля. Определить частоту вращения стержня, при которой разность потенциа­лов между неподвижным концом стержня и его серединой равна 0,1В.

Дано:

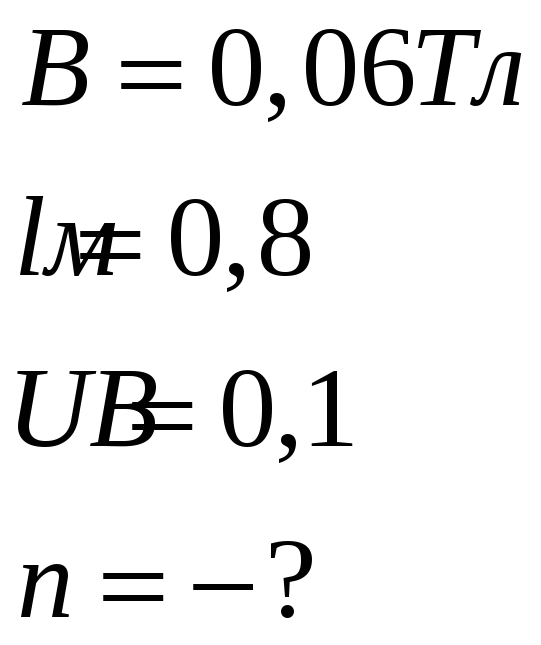
На электроны находящиеся в стержне действуют сила Лоренца и электрическая сила

Скорость электронов на расстоянии от оси вращения

Подставим (2) в (1):

Разность потенциалов