4. Взаимное расположение прямой и плоскости.

4.1. Пересечение прямой с плоскостью.

Пусть дана плоскость и прямая Требуется найти точку пересечения прямой с плоскостью (см. рис.23). Перепишем уравнения прямой в параметрическом виде:

. Подставим полученные выражения в уравнение плоскости:

Возможны три случая:

а). Если это уравнение имеет единственное решение , то прямая пересекает плоскость в точкеM с координатами:

б). Если это уравнение не имеет решений, то прямая параллельна плоскости.

в). Если уравнение имеет бесчисленное множество решений, т.е. имеет вид то прямая лежит в плоскости.

Пример. Найти точку пересечения прямой с плоскостью, если:

а).

б).

в).

Решение: а). Запишем уравнения прямой в параметрическом виде:

Подставим эти уравнения в уравнение плоскости:

2(2 - t) – 4t -2(-1 -3t) – 8 = 0

4 – 2t – 4t +2 + 6t – 8 = 0 Полученное уравнение не имеет решений. Следовательно, прямая параллельна плоскости.

б). Рассуждая аналогично, получим:

(2 + t) + (–4t) + (–1 + 3t) – 1 = 0 t –любое.

Уравнение имеет бесчисленное множество решений. Следовательно, прямая лежит в плоскости.

в). Запишем уравнение в параметрическом виде. Для этого найдем точку, лежащую на прямой. Пустьz = 0. Тогда Итак

Найдем направляющий вектор . Для этого выпишем нормальные векторы плоскостейВычислим их векторное произведение:

Воспользуемся формулами (3.2.1):

Подставим в уравнение плоскости

Получим точку пересечения прямой с плоскостью, подставив найденное значениеt = –1 в параметрические уравнения прямой

Ответ: а). .

б). Прямая лежит в плоскости.

в). Прямая пересекает плоскость в точке M(–1, 1, 2).

4.2. Параллельность прямой и плоскости.

Условие параллельности прямой и плоскости можно получить, используя векторную алгебру. Пусть прямаяL параллельна плоскости () (см. рис.24). Тогда направляющий векторпрямойL перпендикулярен нормальному вектору плоскости. Следовательно, скалярное произведение этих векторов равно нулю. Еслиили

(4.2.1)

Полученное условие является условием параллельности прямой и плоскости.

Пример. Доказать, прямая параллельна плоскости

Решение: Выпишем направляющий вектор прямойL: и нормальный векторплоскостиНайдем скалярное произведение этих векторов:Следовательно, прямаяL параллельна плоскости .

4.3. Перпендикулярность прямой и плоскости.

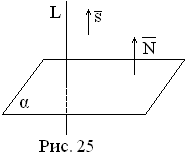
Условие перпендикулярности прямой и плоскости также можно получить, используя векторную алгебру. Пусть прямая L перпендикулярна плоскости (см. рис.25). Тогда направляющий векторпрямойL будет коллинеарен нормальному вектору плоскости. Следовательно, соответствующие координаты этих векторов пропорциональны.

Пусть Тогда

(4.3.1)

Это условие перпендикулярности прямой и плоскости.

Пример 1. Составить уравнение плоскости, проходящей через точку M(1, 2,3)

перпендикулярно прямой .

Решение: Выпишем направляющий вектор прямой: Векторможно взять за нормальный векторискомой плоскости:Применяя формулу (2.1.1), получим

Ответ:

Пример 2. Составить уравнение прямой, проходящей через точку M (2, –1, 0) перпендикулярно плоскости

Решение: Выпишем нормальный векторданной плоскости:Векторможно взять за направляющий вектор искомой прямой:По формулам (3.1.1) запишем канонические уравнения прямой, проходящей через точкуM (2, –1, 0);

Ответ:

52