3.Прямая в пространстве.

3.1. Канонические уравнения прямой.

Пусть в системе координат Oxyz дана прямая, которая проходит через точку

(см. рис.18).Обозначим через вектор, параллельный данной прямой. Векторназываетсянаправляющим вектором прямой. Возьмем на прямой точку и рассмотрим вектор Векторыколлинеарны, следовательно, их соответствующие координаты пропорциональны:

(3.3.1)

Эти уравнения называются каноническими уравнениями прямой.

Пример: Написать уравнения прямой, проходящей через точку M(1, 2, –1) параллельно вектору

Решение: Вектор является направляющим вектором искомой прямой. Применяя формулы (3.1.1), получим:

Это канонические уравнения прямой.

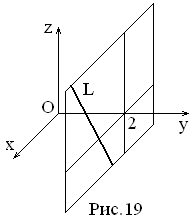
Замечание: Обращение в нуль одного из знаменателей означает обращение в нуль соответствующего числителя, то есть y – 2 = 0; y = 2. Данная прямая лежит в плоскости y = 2, параллельной плоскости Oxz.

3.2. Параметрические уравнения прямой.

Пусть прямая задана каноническими уравнениями

Обозначим тогдаВеличина t называется параметром и может принимать любые значения: .

Выразим x, y и z через t :

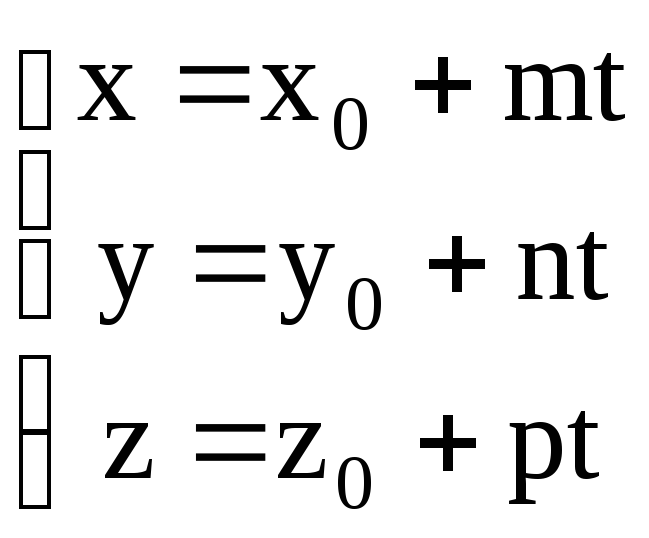(3.2.1)

Полученные уравнения называются параметрическими уравнениями прямой.

Пример 1: Составить параметрические уравнения прямой, проходящей через точку M (1, 2, –1) параллельно вектору

Решение: Канонические уравнения этой прямой получены в примере пункта 3.1:

Для нахождения параметрических уравнений прямой применим вывод формул (3.2.1):

Итак, - параметрические уравнения данной прямой.

Ответ:

Пример 2. Составить параметрические уравнения прямой, проходящей через точку M (–1, 0, 1) параллельно вектору гдеA (2, 1, –1), B (–1, 3, 2).

Решение: Вектор является направляющим вектором искомой прямой.

Найдем вектор .

= (–3; 2; 3). По формулам (3.2.1) запишем уравнения прямой:

- это искомые параметрические уравнения прямой.

3.3. Уравнения прямой, проходящей через две заданные точки.

Через две заданные точки в пространстве проходит единственная прямая (см. рис.20). Пусть даны точки Векторможно принять за направляющий вектор данной прямой. Тогда уравнения прямой находим по формулам (3.1.1):).

(3.3.1)

Пример 1. Составить канонические и параметрические уравнения прямой, проходящей через точки

Решение: Применяем формулу (3.3.1)

Получили канонические уравнения прямой. Для получения параметрических уравнений применим вывод формул (3.2.1). Получим

- это параметрические уравнения прямой.

Пример 2. Составить канонические и параметрические уравнения прямой, проходящей через точки

Решение: По формулам (3.3.1) получим:

Это канонические уравнения.

Переходим к параметрическим уравнениям:

- параметрические уравнения.

Полученная прямая параллельна оси oz (см. рис.21).

3.4. Прямая как линия пересечения двух плоскостей.

Пусть в пространстве даны две плоскости

и

Если эти плоскости не совпадают и не параллельны, то они пересекаются по прямой:

Эта система двух линейных уравнений задает прямую как линию пересечения двух плоскостей. От уравнений (3.4.1) можно перейти к каноническим уравнениям (3.1.1) или параметрическим уравнениям (3.2.1). Для этого необходимо найти точку лежащую на прямой, и направляющий векторКоординаты точкиполучим из системы (3.4.1), придав одной из координат произвольное значение (например,z = 0). За направляющий вектор можно взять векторное произведение векторовто есть

Пример 1. Составить канонические уравнения прямой

Решение: Пусть z = 0. Решим систему

Сложив эти уравнения, получим: 3x + 6 = 0 x = –2. Подставим найденное значение x = –2 в первое уравнение системы и получим: –2 + y + 1 = 0 y = 1.

Итак, точка лежит на искомой прямой.

Для нахождения направляющего вектора прямой запишем нормальные векторы плоскостей: и найдем их векторное произведение:

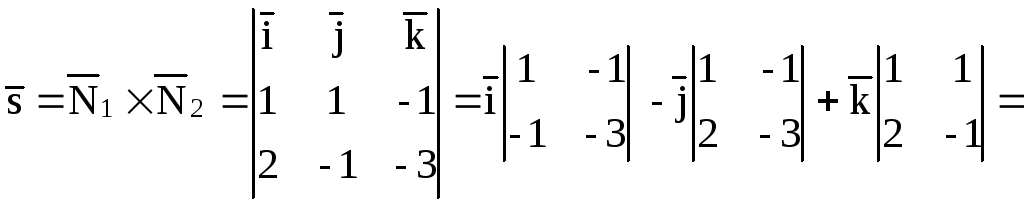
Уравнения прямой находим по формулам (3.1.1):

Ответ: .

Другой способ: Канонические и параметрические уравнения прямой (3.4.1) легко получить, найдя две различные точки на прямой из системы (3.4.1), а затем применив формулы (3.3.1) и вывод формул (3.2.1).

Пример 2. Составить канонические и параметрические уравнения прямой

Решение: Пусть y = 0. Тогда система примет вид:

Сложив уравнения, получим: 2x + 4 = 0; x = –2. Подставим x = –2 во второе уравнение системы и получим: –2 –z +1 = 0 z = –1. Итак, нашли точку

Для нахождения второй точки положим x = 0. Будем иметь:

То есть

Далее применяем формулы (3.3.1):

Получили канонические уравнения прямой.

Составим параметрические уравнения прямой:

Ответ: ; .

3.5. Взаимное расположение двух прямых в пространстве.

Пусть прямые заданы уравнениями:

: ;: .

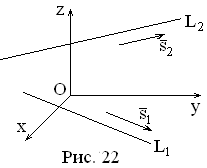
Под углом между этими прямыми понимают угол между их направляющими векторами (см. рис.22). Этот уголнаходим по формуле из векторной алгебры: или

(3.5.1)

Если прямые перпендикулярны (),то Следовательно,

(3.5.2)

Это условие перпендикулярности двух прямых в пространстве.

Если прямые параллельны (),то их направляющие векторы коллинеарны (), то есть

(3.5.3)

Это условие параллельности двух прямых в пространстве.

Пример 1. Найти угол между прямыми:

а). и

б). и

Решение: а). Запишем направляющий вектор прямой Найдем направляющий векторвторой прямой. Для этого находим нормальные векторыплоскостей, входящих в систему Затем найдем их векторное произведение:

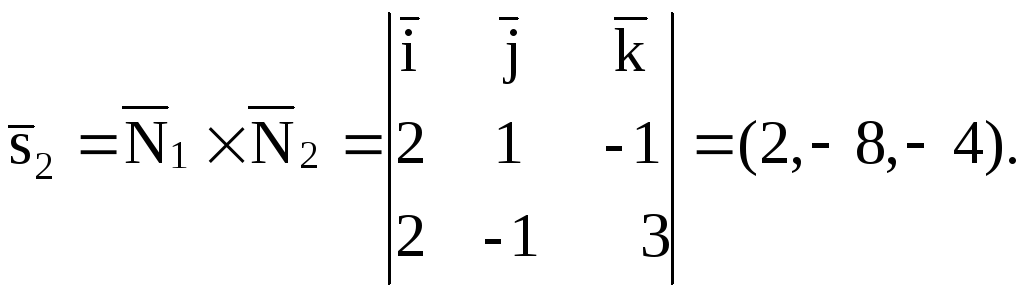(см. пример 1 пункта 3.4).

По формуле (3.5.1) получим:

Следовательно,

б). Запишем направляющие векторы данных прямых: Векторыколлинеарны, так как их соответствующие координаты пропорциональны:

Значит прямые параллельны (), то есть

Ответ: а). б).

Пример 2. Доказать перпендикулярность прямых:

и

Решение: Запишем направляющий вектор первой прямой

Найдем направляющий вектор второй прямой. Для этого находим нормальные векторыплоскостей, входящих в систему: Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие перпендикулярности прямых (3.5.2):

Условие выполнено; следовательно, прямые перпендикулярны ().