Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный строительный университет

Предмет:

Математика

Файл:

Глава 2.doc

Скачиваний:

169

Добавлен:

03.03.2015

Размер:

842.75 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Глава II. Аналитическая геометрия в пространстве.

1. Основные понятия.

Рассмотрим прямоугольную систему координат Oxyz в пространстве.

Уравнением поверхности называется такое уравнение F(x,y,z)=0, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на поверхности.

Например, сфера – это геометрическое место точек, равноудаленных от некоторой точки, называемой центром сферы. Так все точки, удовлетворяющие уравнению лежат на сфере с центром в точке О(0.0.0) и радиусомR (Рис.1).

Координаты любой точки, не лежащей на данной сфере, не удовлетворяют этому уравнению.

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей. Так на рисунке 1 пересечением сферы с плоскостью Oxy является окружность с центром в точке О и радиусом R.

Простейшей поверхностью является плоскость, простейшей линией в пространстве является прямая.

2. Плоскость в пространстве.

2.1. Уравнение плоскости по точке и нормальному вектору.

В системе координат Oxyz рассмотрим плоскость (Рис.2). Ее положение определяется заданием вектораперпендикулярного этой плоскости, и фиксированной точкилежащей в этой плоскости. Вектор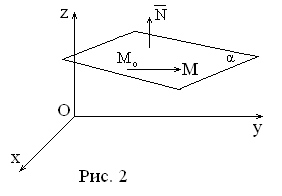перпендикулярный плоскостиназываетсянормальным вектором (вектором-нормалью). Рассмотрим произвольную точку M(x,y,z) плоскости . Векторлежащий в плоскостибудет перпендикулярен вектору-нормалиИспользуя условие ортогональности векторовполучим уравнение:где

Уравнение (2.2.1)

называется уравнением плоскости по точке и нормальному вектору.

Если в уравнении (2.1.1) раскроем скобки и перегруппируем члены, то получим уравнение илиAx + By + Cz + D = 0, где

D = .

2.2. Общее уравнение плоскости.

Уравнение Ax + By + Cz +D = 0 (2.2.1)

называется общим уравнением плоскости, где - нормальный вектор.

Рассмотрим частные случаи этого уравнения.

1).D = 0. Уравнение имеет вид: Ax + By + Cz = 0. Такая плоскость проходит через начало координат. Ее нормальный вектор

2). С = 0 :Ax + By + D = 0 плоскость параллельна оси oz (Рис.3).

3). B = 0 : Ax + Cz + D = 0 плоскость параллельна оси oy (Рис.4).

4). A = 0 : By + Cz + D = 0 плоскость параллельна оси ox (Рис.5).

5). C = D = 0 : Ax + By = 0 плоскость проходит через ось oz (Рис.6).

6).B = D = 0 : Ax + Cz = 0 плоскость проходит через ось oy (Рис.7).

7). A = D = 0 : By + Cz = 0 плоскость проходит через ось ox (Рис.8).

8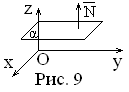).A = B = 0 : Cz + D = 0 ||oz плоскость параллельна плоскостиOxy (Рис.9).

9). B = C = 0 : Ax + D = 0 ||ox плоскость

параллельна плоскостиOyz (Рис.10).

10).A = C = 0 : By + D = 0 ||oy плоскость параллельна плоскостиOxz (Рис.11).

Пример 1. Составить уравнение плоскости, проходящей через точку перпендикулярно векторуНайти точки пересечения этой плоскости с осями координат.

Решение. По формуле (2.1.1) имеем

2x – y + 3z + 3 = 0.

Для того, чтобы найти пересечение этой плоскости с осью ox, подставим в полученное уравнение y = 0, z = 0. Имеем 2x + 3 = 0; x = – 1,5.

Точка пересечения искомой плоскости с осью ox имеет координаты:

Найдем пересечение плоскости с осью oy. Для этого возьмем x = 0; z = 0. Имеем

– y + 3 = 0 y = 3. Итак,

Для нахождения точки пересечения с осью oz возьмем x = 0; y = 0 3z + 3 = 0 z = – 1. Итак,

Ответ: 2x – y + 3z + 3 = 0, ,,.

Пример 2. Исследовать плоскости, заданные уравнениями:

a). 3x – y + 2z = 0

б). 2x + z – 1 = 0

в). – y + 5 = 0

г). x = 0.

Решение. а). Данная плоскость проходит через начало координат (D = 0) и имеет нормальный вектор

б). В уравнении коэффициентB = 0. Следовательно, Плоскость параллельна осиoy.

в). В уравнении – y + 5 = 0 коэффициенты A = 0, C = 0. Значит

Плоскость параллельна плоскости oxz.

г). Уравнение x = 0 задает плоскость oyz, так как при B = 0, C = 0 плоскость параллельна плоскости oyz, а из условия D = 0 следует, что плоскость проходит через начало координат.

Пример 3. Составить уравнение плоскости, проходящей через точку A(2,3,1) и перпендикулярной вектору гдеB(1,0, –1), C(–2,2,0).

Решение. Найдем вектор

Вектор является нормальным вектором искомой плоскости, проходящей через точкуA(2,3,1). По формуле (2.1.1) имеем:

– 3x + 2y + z + 6 – 6 – 1 = 0– 3x + 2y + z – 1 = 0 3x – 2y – z + 1 = 0.

Ответ: 3x – 2y – z + 1 = 0.

2.3. Уравнение плоскости, проходящей через три точки.

Три точки, не лежащие на одной прямой, определяют единственную плоскость (см. рис. 12). Пусть точки не лежат на одной прямой. Чтобы составить уравнение плоскости, нужно знать одну точку плоскости и нормальный вектор. Точки, лежащие на плоскости, известны: Можно взять любую. Для нахождения нормального вектора воспользуемся определением векторного произведения векторов. Пусть Тогдаследовательно,Зная координаты точкии нормального векторанайдем уравнение плоскости, применяя формулу (2.1.1).

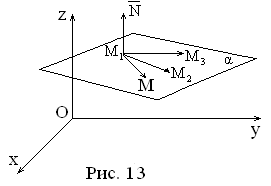Другим способом уравнение плоскости, проходящей через три заданные точки, можно получить, используя условие компланарности трех векторов. Действительно, векторы где M(x,y,z) – произвольная точка искомой плоскости, компланарны (см. рис.13). Следовательно, их смешанное произведение равно 0:

Применив формулу смешанного произведения в координатной форме, получим:

(2.3.1)

Пример 1. Составить уравнение плоскости, проходящей через точки

Решение. По формуле (2.3.1) имеем

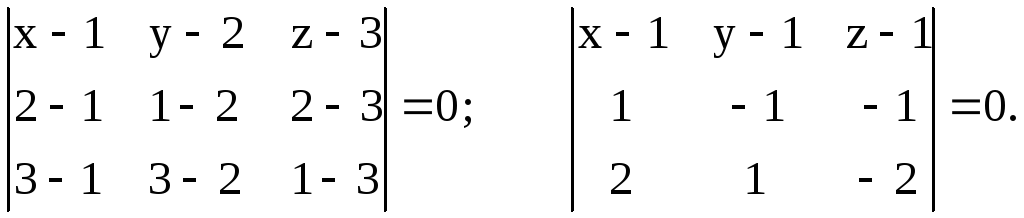
Раскрыв определитель, получим:

Полученная плоскость параллельна оси oy. Ее нормальный вектор

Ответ: x + z – 4 = 0.

2.4. Угол между двумя прямыми.

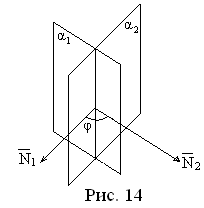Две плоскости, пересекаясь, образуют четыре двугранных угла, равных попарно (см. рис. 14). Один из двугранных углов равен углу между нормальными векторами этих плоскостей.

Пусть даны плоскости:

Их нормальные векторы имеют координаты:

Из векторной алгебры известно, что или

(2.4.1)

Пример: Найти угол между плоскостями:

Решение: Найдем координаты нормальных векторов: По формуле (2.4.1) имеем:

Один из двугранных углов, полученных при пересечении данных плоскостей, равен Можно найти и второй угол:

Ответ:

2.5. Условие параллельности двух плоскостей.

Пусть даны две плоскости:

Если эти плоскости параллельны, то их нормальные векторы

коллинеарны (см. рис.15).

Если векторы коллинеарны, то их соответствующие координаты пропорциональны:

(2.5.1)

Верно и обратное утверждение: если нормальные векторы плоскостей коллинеарны, то плоскости параллельны.

Пример 1. Какие из указанных плоскостей параллельны:

а). ,

б). ?

Решение: а). Выпишем координаты нормальных векторов.

Проверим их коллинеарность:

Отсюда следует, что

б). Выпишем координаты

Проверим коллинеарность:

Векторы не коллинеарны, плоскости не параллельны.

Пример 2. Составить уравнение плоскости, проходящей через точку

M(2, 3, –2) параллельно плоскости

Решение: Искомая плоскость параллельна данной плоскости. Поэтому нормальный вектор плоскости можно взять за нормальный вектор искомой плоскости.Применяя уравнение (2.1.1), получим:

Ответ: .

Пример 3. Определить при каких a и b плоскости параллельны:

Решение: Выпишем координаты нормальных векторов:

Так как плоскости параллельны, то векторы коллинеарны.По условию (2.5.1)Отсюда b = – 2 ; a = 3.

Ответ: a = 3; b = –2.

2.6. Условие перпендикулярности двух плоскостей.

Если плоскости перпендикулярны, то их нормальные векторытоже перпендикулярны (см. рис.16).. Отсюда следует, что их скалярное произведение равно нулю, т.е. или в координатах:

(2.6.1)

Это условие перпендикулярности двух плоскостей. Обратное утверждение также верно, то есть, если выполняется условие (2.6.1), то векторы следовательно,