
- •Московский государственный строительный университет
- •Основные понятия
- •Определение вероятности
- •Пример 1.
- •Решение.
- •Пример 2.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Основные теоремы
- •Решение.
- •Последовательность независимых, однородных испытаний. Схема бернулли
- •Решение.
- •Формула пуассона
- •Решение.
- •Решение.
- •Локальная и интегральная формулы муавра – лапласа
- •Решение.
- •Решение.
- •Случайные величины
- •Нормальное распределение случайной величины
- •Решение.
- •Решение.
- •Рассмотрим решение задач типового варианта. Задание №1 .
- •Решение.
- •Ответ: . Задание №2 .
- •Решение.
- •Ответ: . Задание №3 .
- •Решение.
- •Ответ: .
- •Ответ: ; .
- •I. Задача.
- •Выполнение работы.
- •Приложение №2. Справочные материалы
- •Задачи и упражнения
- •Вопросы по теории вероятностей
Московский государственный строительный университет
_
Кафедра высшей математики
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И
ВЫПОЛНЕНИЮ РАСЧЕТНОГО ЗАДАНИЯ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
Москва 2007
С о с т а в и т е л и:
доцент, кандидат физико-математических наук Е.Е.Ассеева,
профессор, кандидат физико-математических наук М.Л.Каган,
доцент Т.А.Мацеевич
ВВЕДЕНИЕ
Настоящие методические указания по разделу «Теория вероятностей» курса высшей математики предназначены для самостоятельной работы студентов заочного отделения над практической частью курса и выполнения расчетного задания.
Выполнять задание следует точно в сроки, установленные планом учебных занятий. Выполнять задание надо в отдельной тетрадке, вклеив в нее текст варианта. Решения должны быть по возможности краткими, с указанием теоретических положений, используемых при решении задач. При защите задания студент должен уметь объяснить решение каждой задачи и ответить на связанные с ней теоретические вопросы.
Для облегчения самостоятельной работы над выполнением задания ниже приведены формулировки определений, основных теорем и разобраны типовые задачи.
При выполнении расчетов целесообразно пользоваться калькулятором и соответствующими таблицами. Краткие варианты таблиц даны в качестве приложений в конце методических указаний.
При подготовке к зачету весьма полезно проверить свои знания, ответив на вопросы, которые приведены в методических указаниях в разделе «Вопросы для самостоятельной работы».
Основные понятия
Стохастическим называется эксперимент, результаты которого заранее (до его проведения ) не известны.
Случайным событием называется явление, которое может произойти или не произойти в результате стохастического эксперимента.
Случайные события обозначают большими буквами А, В, С и т.д.
Предположим, что среди всех возможных событий, которые в данном опыте могут произойти или не произойти, можно выделить совокупность так называемых элементарных событий, которые обладают следующими свойствами:
взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий;
каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А.
Элементарные
события обозначают греческой буквой
![]() ,
совокупность элементарных событий
называют пространством элементарных
событий и обозначают буквой
,
совокупность элементарных событий
называют пространством элементарных
событий и обозначают буквой![]() .
.
Алгебра событий
Пусть
![]() - пространство элементарных событий
рассматриваемого опыта. Событие А
состоит в том, что произошло одно из
элементарных событий.
- пространство элементарных событий
рассматриваемого опыта. Событие А
состоит в том, что произошло одно из
элементарных событий.
Событие
называется достоверным,
если оно наступает в результате появления
любого элементарного события. Тогда
ему благоприятствует любое событие
![]() ,
достоверное событие будем обозначать
,
достоверное событие будем обозначать![]() .
.
Невозможным
событием
будем называть событие, не наступающее
ни при каком элементарном событии.
Невозможное событие будем обозначать
символом
![]() .
.
Суммой
(или объединением) двух событий А и В
назовем событие А+В (или А![]() В),
происходящее тогда и только тогда, когда
происходит или А или В. Сумме событий
соответствует объединение множеств А
и В.
В),
происходящее тогда и только тогда, когда
происходит или А или В. Сумме событий
соответствует объединение множеств А
и В.
Свойства суммы событий:
А+
 =А;
=А;А+
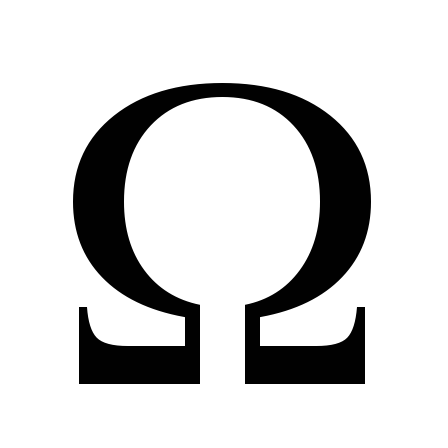 =
= ;
;А+А=А;
А+В=В+А.
Произведением
(или
пересечением) двух событий А и В назовем
событие АВ (или А![]() В),
которое происходит тогда и только тогда,
когда происходит и А, и В. Произведению
событий соответствует пересечение
множеств А и В.
В),
которое происходит тогда и только тогда,
когда происходит и А, и В. Произведению
событий соответствует пересечение
множеств А и В.
Свойства произведения событий:
А
 ;
;А
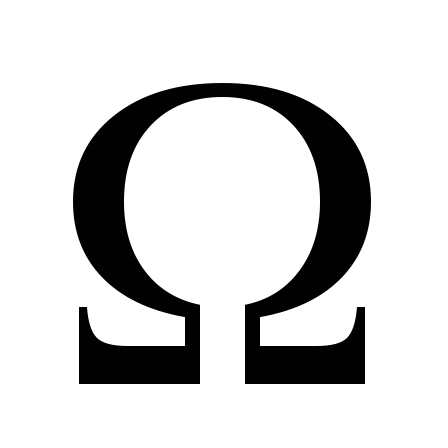 =А;
=А;АА=А;
АВ=ВА.
Два события назовем
несовместными,
если их одновременное появление в опыте
не возможно. Если А и В несовместны, то
АВ=![]() .
Элементарные события попарно несовместны
.
Элементарные события попарно несовместны![]() ,
при
,
при![]() .
.
Событие
![]() назовемпротивоположным
к А, если оно происходит тогда и только
тогда, когда А не происходит. Очевидно,
что выполняются следующие равенства
назовемпротивоположным
к А, если оно происходит тогда и только
тогда, когда А не происходит. Очевидно,
что выполняются следующие равенства
![]() ,
,
![]() ,
,![]() .
.
Разностью
событий А и В назовем событие А\В,
происходящее тогда и только тогда, когда
происходит А, но не происходит В. Отметим
очевидные соотношения:
![]() ,
,
![]() .
.
Введенные операции сложения и умножения обладают свойствами:
А(В+С)=АВ+АС;
А(ВС)=(АВ)С.
Рассмотрим
пространство элементарных событий
![]() ,
соответствующее некоторому эксперименту
и пусть
,
соответствующее некоторому эксперименту
и пусть![]() - некоторая система случайных событий.
- некоторая система случайных событий.
Систему![]() событий назовем
алгеброй событий,
если выполняются следующие условия:
событий назовем
алгеброй событий,
если выполняются следующие условия:
1)
![]() ;
;
2) если
![]() ,
то
,
то![]() ;
;
3) если
![]() ,
,![]() ,
то
,
то![]() ,
,![]() .
.
