
5. Задачи и упражнения к главе II.
1. Найти уравнение
плоскости, проходящей через данную
точку
![]() параллельно двум данным (неколлинеарным)
векторам
параллельно двум данным (неколлинеарным)
векторам![]()
 Указание:
1способ.
Возьмем произвольную точку плоскости
M
(x,
y,
z).
Векторы
Указание:
1способ.
Возьмем произвольную точку плоскости
M
(x,
y,
z).
Векторы
![]() будут компланарны, так как они расположены
в параллельных плоскостях. Следовательно,
их смешанное произведение
будут компланарны, так как они расположены
в параллельных плоскостях. Следовательно,
их смешанное произведение![]() Записывая это условие в координатах,
получим уравнение искомой плоскости:
Записывая это условие в координатах,
получим уравнение искомой плоскости: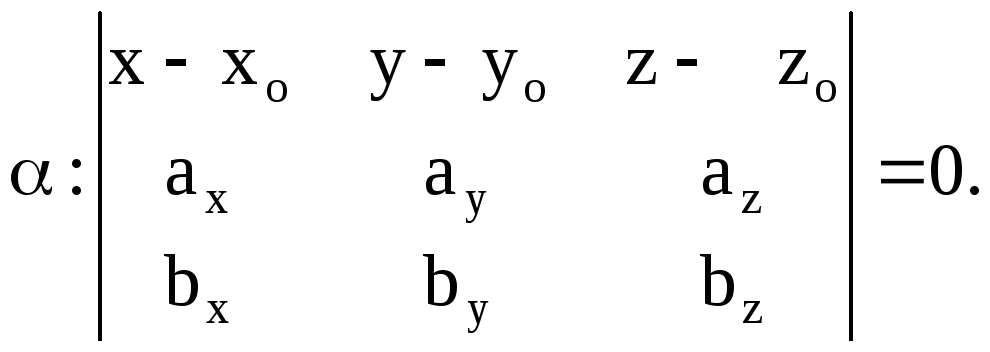
Вычислять этот определитель удобнее разложением по первой строке.
2 способ.
Векторы
![]() параллельны искомой плоскости.
Следовательно, вектор, равный векторному
произведению векторов
параллельны искомой плоскости.
Следовательно, вектор, равный векторному
произведению векторов![]() перпендикулярен этой плоскости
перпендикулярен этой плоскости![]() ,
т.е.
,
т.е.![]() и
и![]() . Вектор
. Вектор![]() является нормальным вектором плоскости
является нормальным вектором плоскости![]() .
Если
.
Если![]() и
и ![]() ,
то вектор
,
то вектор
![]() находится по формуле:
находится по формуле:

Уравнение плоскости
![]() находим по точке
находим по точке![]() и нормальному
вектору
и нормальному
вектору
![]()
![]() (2.1.1).
(2.1.1).
2. Найти уравнение
плоскости, проходящей через две данные
точки ![]() параллельно данному вектору
параллельно данному вектору ![]() .(
.(![]() неколлинеарны).
неколлинеарны).
 Указание:
1 способ.
Пусть M
(x,
y,
z)
– произвольная точка плоскости. Тогда
векторы
Указание:
1 способ.
Пусть M
(x,
y,
z)
– произвольная точка плоскости. Тогда
векторы ![]() и
и ![]() располагаются в
параллельных плоскостяхи,
следовательно, компланарны, т.е. их
смешанное произведение
располагаются в
параллельных плоскостяхи,
следовательно, компланарны, т.е. их
смешанное произведение
![]() Записав это условие
в координатах, получим уравнение искомой
плоскости
Записав это условие
в координатах, получим уравнение искомой
плоскости
![]() .
.

2 способ.
Вектор
нормали к искомой плоскости будет равен
векторному произведению векторов ![]() ,
т.е.
,
т.е.
![]() или в координатах:
или в координатах:

Уравнение искомой
плоскости
![]() найдется по нормальному вектору
найдется по нормальному вектору![]() и точке
и точке![]() (или точке
(или точке![]() )по формуле (2.1.1)
)по формуле (2.1.1)
![]() (см. пример 1 пункт
2.2).
(см. пример 1 пункт
2.2).
3. Найти уравнение
плоскости, проходящей через точку
![]() параллельно плоскости 2x
– 6y
– 3z
+5 =0.
параллельно плоскости 2x
– 6y
– 3z
+5 =0.
Указание:
Нормальный вектор
![]() найдем из общего уравнения данной
плоскости 2x
– 6y
– 3z
+5 =0 (2.2.1).
найдем из общего уравнения данной
плоскости 2x
– 6y
– 3z
+5 =0 (2.2.1).
![]() Вектор
Вектор![]() перпендику-лярен данной плоскости,
следовательно, он перпендикулярен любой
плоскости, параллельной ей. Вектор
перпендику-лярен данной плоскости,
следовательно, он перпендикулярен любой
плоскости, параллельной ей. Вектор![]() можно взять за нормальный вектор искомой
плоскости. Составим уравнение искомой
плоскости по точке
можно взять за нормальный вектор искомой
плоскости. Составим уравнение искомой
плоскости по точке![]() и
нормальному вектору
и
нормальному вектору![]() (см. пример 1 пункт 2.2).
(см. пример 1 пункт 2.2).
![]()
Ответ:
![]()
4. Составить
уравнение плоскости, проходящей через
точку
![]() перпендикулярно линии пересечения
плоскостей 2x
+ y
– 2z
+ 1 =0 и
перпендикулярно линии пересечения
плоскостей 2x
+ y
– 2z
+ 1 =0 и
x + y + z – 5 = 0.
 Указание:
1 способ.
Перпендикулярные каждый своей плоскости
векторы
Указание:
1 способ.
Перпендикулярные каждый своей плоскости
векторы
![]() (координаты
векторов найдены из общих уравнений
плоскостей, формула (2.2.1)) перпендикулярны
линии их пересечения и, следовательно,
параллельны искомой плоскости. Искомая
плоскость проходит через точку
(координаты
векторов найдены из общих уравнений
плоскостей, формула (2.2.1)) перпендикулярны
линии их пересечения и, следовательно,
параллельны искомой плоскости. Искомая
плоскость проходит через точку![]() параллельно двум векторам
параллельно двум векторам![]() (см. задачу 1 пункт 5).
(см. задачу 1 пункт 5).
![]()
![]() Уравнение
искомой плоскости имеет вид:
Уравнение
искомой плоскости имеет вид:

Раскрывая определитель третьего порядка по первой строке, получим искомое уравнение.
![]()
![]()
![]()
2 способ.
Составим уравнение плоскости по точке
![]() и нормальному
вектору
и нормальному
вектору
![]() по формуле (2.2.1). Нормальный вектор
по формуле (2.2.1). Нормальный вектор![]() равен векторному произведению векторов
равен векторному произведению векторов![]() ,т.е.
,т.е. ![]() Так как векторы
Так как векторы![]() перпендикулярны
линии пересечения плоскостей, то вектор
перпендикулярны
линии пересечения плоскостей, то вектор
![]() параллелен линии пересечения плоскостей
и перпендикулярен искомой плоскости.
параллелен линии пересечения плоскостей
и перпендикулярен искомой плоскости.
Векторы ![]() (см. формулу 2.2.1),
тогда
(см. формулу 2.2.1),
тогда

![]()
Составим уравнение
плоскости по точке ![]() и нормальному
вектору
и нормальному
вектору
![]() (см. пример 1 пункт
2.2)
(см. пример 1 пункт
2.2)
![]()
![]()
Ответ:
![]()
![]()
5. Найти уравнение
плоскости, проходящей через точки ![]() и
и
![]() перпендикулярно плоскости 3x
– y
+ 3z
+15 = 0.
перпендикулярно плоскости 3x
– y
+ 3z
+15 = 0.
Указание:
1 способ.
Выпишем координаты нормального вектора
данной п лоскости
лоскости
![]() 3x
– y
+ 3z
+15 = 0:
3x
– y
+ 3z
+15 = 0:
![]() Так как плоскости перпендикулярны, то
вектор
Так как плоскости перпендикулярны, то
вектор![]() параллелен искомой плоскости
параллелен искомой плоскости![]() Составим уравнение искомой плоскости
Составим уравнение искомой плоскости![]() которая параллельна вектору
которая параллельна вектору![]() и проходит через точки
и проходит через точки![]() (см. решение задачи 2 пункт 5; 1 способ).
(см. решение задачи 2 пункт 5; 1 способ).

Вычисляя определитель, получим уравнение искомой плоскости
![]() 10x
+ 15y
– 5z
– 70 =0
10x
+ 15y
– 5z
– 70 =0
![]() 2x +
3y – z – 14 =0.
2x +
3y – z – 14 =0.
2 способ.
Составим уравнение искомой плоскости
![]() по точке
по точке![]()
 и вектору нормали
и вектору нормали
![]() Вектор
Вектор![]()

![]()
Составляем уравнение
искомой плоскости
![]() .
.
![]() 10(x
– 2) +15(y
– 3) – 5(z
+ 1) = 0;
10(x
– 2) +15(y
– 3) – 5(z
+ 1) = 0;
![]() 10x
+ 15y
– 5z
– 70 = 0 (см. задачу 2 пункт 5; 2 способ).
Разделим обе части уравнения на 5.
10x
+ 15y
– 5z
– 70 = 0 (см. задачу 2 пункт 5; 2 способ).
Разделим обе части уравнения на 5.
![]() 2x
+ 3y
– z
– 14 = 0.
2x
+ 3y
– z
– 14 = 0.
Ответ: 2x + 3y – z – 14 = 0.
6. Составить
уравнение плоскости, проходящей через
точки ![]()
![]() и
и ![]()
Указание: Составим уравнение плоскости, проходящей через три точки (см. пример 1, пункт 2.3, формула 2.3.1).

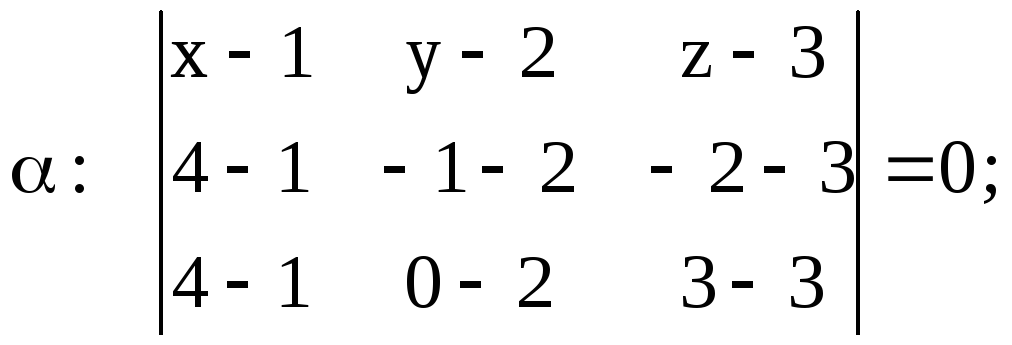

Раскрывая определитель, получим
![]()
Ответ: ![]()
Замечание. Для проверки правильности вычисления определителя рекомендуется в полученное уравнение подставить координаты данных точек, через которые проходит плоскость. Должно получиться тождество; в противном случае в вычислениях допущена ошибка.
7. Составить
уравнение плоскости, проходящей через
точку
![]() параллельно плоскостиx
– 4y
+ 5z
+ 1 = 0.
параллельно плоскостиx
– 4y
+ 5z
+ 1 = 0.
 Указание:
Из общего уравнение данной плоскости
Указание:
Из общего уравнение данной плоскости
![]() x
– 4y
+ 5z
+ 1 = 0 найдем нормальный вектор
x
– 4y
+ 5z
+ 1 = 0 найдем нормальный вектор
![]() (формула 2.2.1). Вектор
(формула 2.2.1). Вектор![]() перпендикулярен к искомой плоскости
перпендикулярен к искомой плоскости![]() Составим
уравнение плоскости по точке
Составим
уравнение плоскости по точке![]() и
нормальному вектору
и
нормальному вектору
![]() (см. пример 1; пункт 2.2):
(см. пример 1; пункт 2.2):
![]() x
– 4y
+ 5z
+ 15 = 0.
x
– 4y
+ 5z
+ 15 = 0.
Ответ: x – 4y + 5z + 15 = 0.
8. Составить
уравнение плоскости, проходящей через
точку
![]() параллельно векторам
параллельно векторам![]()
Указание: См. решение задачи 1 пункт 5. Решаем задачу одним из указанных способов.
Ответ: x – y – z – 1 = 0.
9 .
Составить уравнение плоскости, проходящей
через точку
.
Составить уравнение плоскости, проходящей
через точку![]() перпендикулярно линии пересечения
плоскостей 3x
– 2y
– z
+ 1 = 0 и x
– y
– z
= 0.
перпендикулярно линии пересечения
плоскостей 3x
– 2y
– z
+ 1 = 0 и x
– y
– z
= 0.
Указание: См. решение задачи 4 пункт 5. Решаем задачу одним из указанных способов.
Ответ: x +2y – z – 8 = 0.
10. Найти уравнение
плоскости, проходящей через точки
![]()
![]() перпендикулярно плоскости 3x
– y
– 4z
= 0.
перпендикулярно плоскости 3x
– y
– 4z
= 0.
Указание: См. решение задачи 5 пункт 5.
Ответ: 9x – y +7z – 40 = 0.
1 1.
Найти уравнение плоскости, проходящей
через точки
1.
Найти уравнение плоскости, проходящей
через точки![]()
![]() параллельно
прямой, определяемой точками A
(5; –2; 3) и B
( 6; 1; 0).
параллельно
прямой, определяемой точками A
(5; –2; 3) и B
( 6; 1; 0).
Указание:
Искомая плоскость параллельна прямой
AB,
следовательно, она параллельна вектору
![]() Уравнение искомой плоскости
Уравнение искомой плоскости![]() находим, как в задаче 2 пункта 5 (одним
из способов).
находим, как в задаче 2 пункта 5 (одним
из способов).
Ответ: 3x – 4y – 3z +4 = 0.
1 2.
ТочкаP
(2; –1; –2) служит основанием перпендикуляра,
опущенного из начала координат на
плоскость. Составить уравнение этой
плоскости.
2.
ТочкаP
(2; –1; –2) служит основанием перпендикуляра,
опущенного из начала координат на
плоскость. Составить уравнение этой
плоскости.
Указание:
Нормальным вектором
![]() к искомой плоскости является вектор
к искомой плоскости является вектор![]() Найдем его координаты.P
(2; –1; –2) и O(0;
0; 0)
Найдем его координаты.P
(2; –1; –2) и O(0;
0; 0)
![]()
![]() т.е.
т.е.
![]() Составим уравнение плоскости
Составим уравнение плоскости![]() по точке и нормальному вектору
по точке и нормальному вектору![]() (см. пример 1, пункт
2.2).
(см. пример 1, пункт
2.2).
Ответ: 2x – y – 2z – 9 = 0.
13. Составить
уравнение плоскости, проходящей через
точку
![]() параллельно плоскости: а)xoy;
б) yoz;
в) xoz.
параллельно плоскости: а)xoy;
б) yoz;
в) xoz.
 Указание:
Вектор
Указание:
Вектор
![]() –
единичный вектор осиoz
перпендикулярен плоскости xoy,
следовательно, он перпендикулярен
искомой плоскости
–
единичный вектор осиoz
перпендикулярен плоскости xoy,
следовательно, он перпендикулярен
искомой плоскости
![]() Составляем уравнение плоскости по точкеA
( 0; –1; 2) и
Составляем уравнение плоскости по точкеA
( 0; –1; 2) и
![]() =
(0; 0; 1), т.к.
=
(0; 0; 1), т.к.
![]() (см. решение задачи 3, пункт 5).
(см. решение задачи 3, пункт 5).![]() z –
2 = 0.
z –
2 = 0.
Аналогично решаем задачи б) и в).
б)
![]() где
где![]() (1;
0; 0).
(1;
0; 0).
![]()
в)
![]() где
где![]() (0;
1;
0).
(0;
1;
0).
![]() y
+ 1 = 0.
y
+ 1 = 0.
Ответ: а) z – 2 = 0 ; б) x = 0; в) y + 1 = 0.
14. Составить
уравнение плоскости, проходящей через
точки
![]() и
и
B (2; 1; –1) перпендикулярно плоскости : а) xoy; б) xoz.
Указание: Нормальным вектором плоскости xoy является вектор
![]() =
(0; 0; 1) – единичный вектор оси oz.
Составим уравнение плоскости, проходящей
через две точки
=
(0; 0; 1) – единичный вектор оси oz.
Составим уравнение плоскости, проходящей
через две точки ![]() и B
(2; 1; –1) и перпендикулярной плоскости,
имеющей нормальный вектор
и B
(2; 1; –1) и перпендикулярной плоскости,
имеющей нормальный вектор
![]() (0; 0; 1), используя один из способов решения
задачи 5 пункта 5.
(0; 0; 1), используя один из способов решения
задачи 5 пункта 5.![]() y
– 1 = 0.
y
– 1 = 0.
Аналогично для
задачи б):
![]() где
где
![]() = ( 0; 1; 0).
= ( 0; 1; 0).![]()
Ответ: а) y – 1 = 0 ; б) x + z – 1 = 0.
15. Составить
уравнение плоскости, проходящей через
точки
![]() и
и
B (2; 3; –1) параллельно оси oz.
Указание:
На оси oz
можно взять единичный вектор
![]() = (0; 0; 1). Решение задачи аналогично решению
задачи 2 пункт 5 (любым способом).
= (0; 0; 1). Решение задачи аналогично решению
задачи 2 пункт 5 (любым способом).
Ответ: x – y + 1 = 0.
16. Составить
уравнение плоскости, проходящей через
ось ox
и точку
![]()
Указание:
Плоскость
![]() проходит через осьox,
следовательно, и через точку O(0;
0; 0). На оси ox
можно взять единичный вектор
проходит через осьox,
следовательно, и через точку O(0;
0; 0). На оси ox
можно взять единичный вектор
![]() = (1; 0; 0). Уравнение искомой плоскости
составляем по двум точкамA(2;
–1; 6) и O(0;
0; 0) и вектору
= (1; 0; 0). Уравнение искомой плоскости
составляем по двум точкамA(2;
–1; 6) и O(0;
0; 0) и вектору
![]() параллельному плоскости. (См. решение
задачи 2 пункт 5).
параллельному плоскости. (См. решение
задачи 2 пункт 5).
Ответ: 6y + z = 0.
17. При каком значении А плоскости Ax + 2y – 7z – 1 = 0 и 2x – y + 2z = 0 будут перпендикулярны?
Указание: Из общих уравнений плоскостей
![]() Ax
+ 2y
– 7z
– 1 = 0 и
Ax
+ 2y
– 7z
– 1 = 0 и
![]() 2x
– y
+ 2z
= 0 векторы нормалей
2x
– y
+ 2z
= 0 векторы нормалей
![]() =
(А; 2; –7) и
=
(А; 2; –7) и
![]() =
( 2; –1; 2) (2.2.1). Условие перпендикулярности
двух плоскостей
=
( 2; –1; 2) (2.2.1). Условие перпендикулярности
двух плоскостей![]()
![]() (2.6.1).
(2.6.1).
![]()
Ответ: A = 8.
18. При каком значении А плоскости 2x + 3y – 6z – 23 = 0 и
4x + Ay – 12z + 7 = 0 будут параллельны?
Указание:
![]() 2x
+ 3y
– 6z
– 23 = 0 и
2x
+ 3y
– 6z
– 23 = 0 и
![]() 4x
+ Ay
– 12y
+ 7 = 0
4x
+ Ay
– 12y
+ 7 = 0
![]()
![]() = (2; 3; –6) и
= (2; 3; –6) и
![]()
![]() =
(4;A;
–12)
(2.2.1). Т.к.
=
(4;A;
–12)
(2.2.1). Т.к.
![]() (2.5.1)
(2.5.1)
![]()
![]()
Ответ: A = 6.
19. Найти угол между двумя плоскостями 2x + y + z + 7 = 0 и x – 2y + 3z = 0.
Указание:
![]() 2x
+ y
+ z
+ 7 = 0 и
2x
+ y
+ z
+ 7 = 0 и
![]() x
– 2y
+ 3z
= 0
x
– 2y
+ 3z
= 0
![]()
![]() = (2;
1;
1)
и
= (2;
1;
1)
и
![]()
![]() =
(1;
–2;
3)
=
(1;
–2;
3)
![]()
![]() (2.4.1)
(2.4.1)
![]()
Ответ:
![]()
20. Составить канонические уравнения прямой, проходящей через точку
A
(1;
2; –3)
параллельно
вектору
![]() =(1;
–2;
1).
=(1;
–2;
1).
Указание: См. решение примера пункта 3.1.
Ответ:
![]()
21. Составить параметрические уравнения прямой, проходящей через точку
A
( –2; 3; 1) параллельно вектору
![]() =(3;
–1; 2).
=(3;
–1; 2).
Указание: См. решение примера пункта 3.2.
Ответ:
 .
.
22. Составить канонические и параметрические уравнения прямой, проходящей через точки A (1; 0; –2) и B (1; 2; –4) .
Указание: См. решение примера 1 пункта 3.3.
Ответ: а)
![]() б)
б)
23. Составить канонические и параметрические уравнения прямой, заданной как пересечение двух плоскостей x – 2y +3z – 4 = 0 и 3x + 2y – 5z – 4 = 0.
Указание:
См. пример 1 пункт 3.4. Пусть z
= 0, тогда координаты x
и y
точки
![]() находим из решения системы
находим из решения системы![]()
Следовательно,
точка
![]() ,
лежащая на искомой прямой, имеет
координаты
,
лежащая на искомой прямой, имеет
координаты
![]() (2;
–1; 0). Для нахождения направляющего
вектора искомой прямой из общих уравнений
плоскостей
(2;
–1; 0). Для нахождения направляющего
вектора искомой прямой из общих уравнений
плоскостей
![]() x
– 2y
+3z
– 4 = 0 и
x
– 2y
+3z
– 4 = 0 и
![]() 3x
+ 2y
– 5z
– 4 = 0
3x
+ 2y
– 5z
– 4 = 0
находим нормальные
векторы
![]() =(1;
–2;
3) и
=(1;
–2;
3) и
![]() =(3;
2; –5).
=(3;
2; –5).
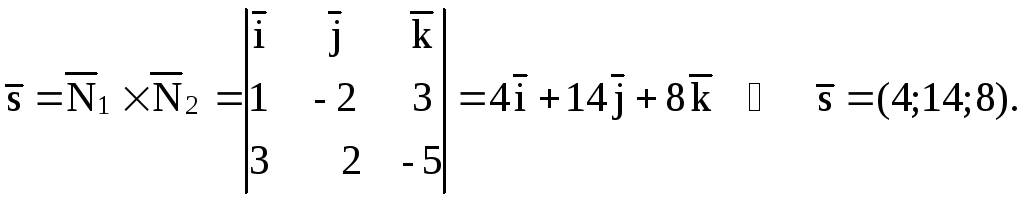
Канонические
уравнения прямой находим по точке
![]() (2;
–1; 0) и направля-ющему вектору
(2;
–1; 0) и направля-ющему вектору![]()
![]() (См. формулу
(3.1.1)).
(См. формулу
(3.1.1)).
Параметрические
уравнения прямой можно найти по формуле
(3.2.1) или из канонических уравнений: ![]() Имеем:
Имеем:

Ответ:
![]() ;
;  .
.
24. Через точку
![]() (2;
–3; –4) провести прямую, параллельную
прямой
(2;
–3; –4) провести прямую, параллельную
прямой
![]() .
.
Указание:
Канонические уравнения искомой прямой
![]() найдем по точке
найдем по точке![]()
 и направляющему вектору
и направляющему вектору![]() Так как
Так как![]() то за направляющий вектор
то за направляющий вектор![]() прямой
прямой![]() можно
взять направляющий вектор
можно
взять направляющий вектор![]() прямойL.
Далее см. решение задачи 23 пункт 5 или
пример 1 пункт 3.4.
прямойL.
Далее см. решение задачи 23 пункт 5 или
пример 1 пункт 3.4.
Ответ:
![]()
25. Даны вершины треугольника A (–5; 7; 1), B (2; 4; –1) и C (–1; 3; 5). Найти уравнение медианы треугольника ABC, проведенной из вершины B.
Указание: Координаты точки M найдем из условия AM = MC (BM – медиана треугольника ABC).

С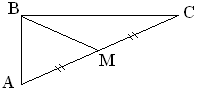 оставим
канонические уравнения прямойBM
по двум точкам B
(2; 4; –1) и
оставим
канонические уравнения прямойBM
по двум точкам B
(2; 4; –1) и ![]() (См. пример 1 пункт
3.3).
(См. пример 1 пункт
3.3).
Ответ:
![]()
26. Составить
канонические и параметрические уравнения
прямой, проходящей через точку
![]() (–1;
–2; 2) параллельно осиox.
(–1;
–2; 2) параллельно осиox.
Указание:
Вектор
![]() – единичный вектор осиox
параллелен искомой прямой. Следовательно,
его можно принять за направляющий вектор
прямой
– единичный вектор осиox
параллелен искомой прямой. Следовательно,
его можно принять за направляющий вектор
прямой
![]() = (1; 0; 0). Составим уравнения прямой по
точке
= (1; 0; 0). Составим уравнения прямой по
точке
![]() (–1;
–2: 2) и вектору
(–1;
–2: 2) и вектору
![]() = (1; 0; 0) (см. пример пункт 3.1 и пример 1
пункт 3.2).
= (1; 0; 0) (см. пример пункт 3.1 и пример 1
пункт 3.2).
Ответ:
![]() ;
; 
27. Составить
канонические уравнения прямой, проходящей
через точку
![]() (3;
–2; 4) перпендикулярно плоскости 5x
+ 3y
– 7z
+ 1 = 0.
(3;
–2; 4) перпендикулярно плоскости 5x
+ 3y
– 7z
+ 1 = 0.
 Указание:
Из общего уравнения плоскости
Указание:
Из общего уравнения плоскости
![]() 5x
+ 3y
– 7z
+ 1 = 0 найдем нормальный вектор
5x
+ 3y
– 7z
+ 1 = 0 найдем нормальный вектор
![]() =
(5; 3; –7). По условию искомая прямая
=
(5; 3; –7). По условию искомая прямая![]() следовательно, вектор
следовательно, вектор![]() т.е. вектор
т.е. вектор![]() является направляющим вектором прямойL:
является направляющим вектором прямойL:
![]() = (5; 3; –7). Составляем канонические
уравнения прямой по точке
= (5; 3; –7). Составляем канонические
уравнения прямой по точке![]() (3;
–2; 4) и направляющему вектору
(3;
–2; 4) и направляющему вектору
![]() = (5; 3; –7). (См. пример
пункт 3.1).
= (5; 3; –7). (См. пример
пункт 3.1).
Ответ:
![]()
28. Составить параметрические уравнения перпендикуляра, опущенного из начала координат на плоскость 4x – y + 2z – 3 = 0.
Указание:
Составим
уравнение искомого перпендикуляра,
т.е. прямой, перпендикулярной плоскости
![]() 4x
– y
+ 2z
– 3 = 0 и проходящей через точку O
(0; 0; 0). (См. решение задачи 27 пункт 5 и
примера 1 пункт 3.2).
4x
– y
+ 2z
– 3 = 0 и проходящей через точку O
(0; 0; 0). (См. решение задачи 27 пункт 5 и
примера 1 пункт 3.2).
Ответ:
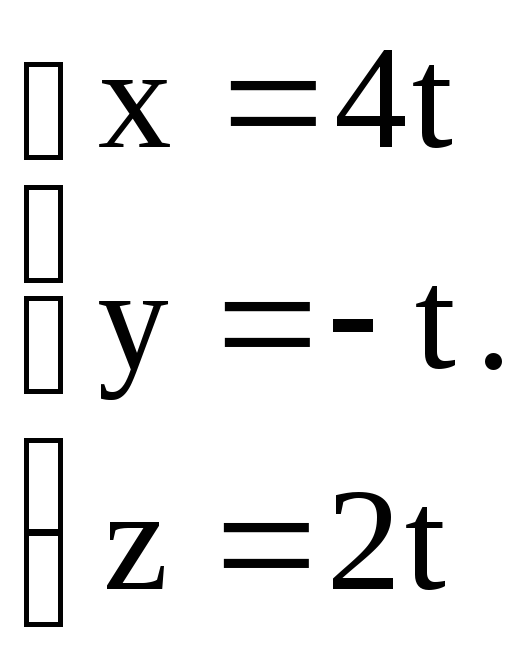
29. Найти точку
пересечения прямой ![]() и плоскости
и плоскости
x – 2y + z – 15 = 0.
 Указание:
Чтобы найти точку M
пересечения прямой
Указание:
Чтобы найти точку M
пересечения прямой
L:
![]() и плоскости
и плоскости
![]() x
– 2y
+ z
– 15 = 0, надо решить систему уравнений:
x
– 2y
+ z
– 15 = 0, надо решить систему уравнений:
 ;
;
Для решения системы канонические уравнения прямой преобразуем к параметрическим уравнениям. (См. задачу 23 пункт 5).



Ответ:
![]()
30. Найти проекцию точки M (4; –3; 1) на плоскость x + 2y – z – 3 = 0.
Указание:
Проекцией точки М на плоскость будет
точка P
– точка п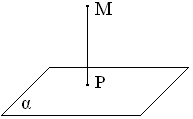 ересечения
перпендикуляра, опущенного из точки М
на плоскость
ересечения
перпендикуляра, опущенного из точки М
на плоскость![]() и плос-кости
и плос-кости![]() Составим параметрические уравнения
пер-пендикуляра МР.(См. решение задачи
28 пункт 5).
Составим параметрические уравнения
пер-пендикуляра МР.(См. решение задачи
28 пункт 5).
Найдем точку Р –
точку пересечения прямой МР и плоскости
![]() (См. решение задачи 29 пункт 5).
(См. решение задачи 29 пункт 5).
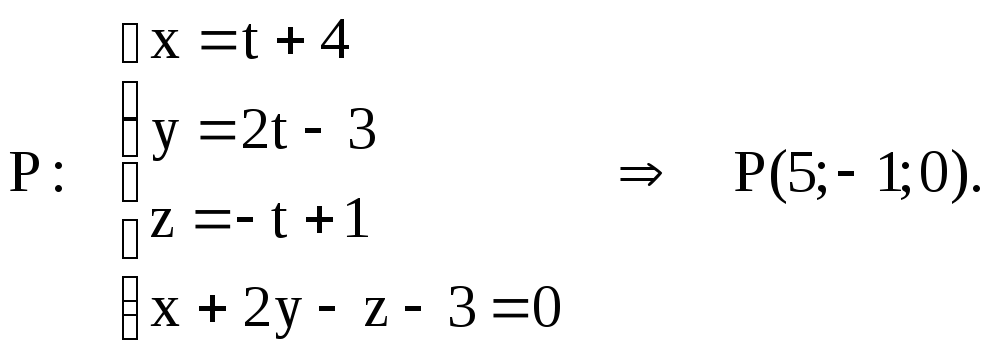
Ответ: ![]()
31. Найти проекцию
точки А(1; 2; 1) на прямую ![]()
Указание:
Проекцией
точки А на прямую L:
![]() является т
является т очкаВ пересечения
прямой L
и плоскости
очкаВ пересечения
прямой L
и плоскости
![]() которая проходит через точку А и
перпендикулярна прямойL.
Из канонических уравнений прямой L
выпишем направляющий вектор
которая проходит через точку А и
перпендикулярна прямойL.
Из канонических уравнений прямой L
выпишем направляющий вектор
![]()
![]() =(3;
–1; 2). Плоскость
=(3;
–1; 2). Плоскость![]() перпендикулярна прямойL,
следовательно,
перпендикулярна прямойL,
следовательно,
![]() Таким образом, вектор
Таким образом, вектор![]() можно взять за нормальный вектор
плоскости
можно взять за нормальный вектор
плоскости![]()
![]() =
(3; –1; 2). Составим уравнение плоскости
=
(3; –1; 2). Составим уравнение плоскости![]() по точке А(1; 2; 1) и
по точке А(1; 2; 1) и![]() =
(3; –1; 2) (см. пример 1 пункт 2.2):
=
(3; –1; 2) (см. пример 1 пункт 2.2):![]() 3(x
– 1) – 1(y
– 2) + 2(z
– 1) = 0
3(x
– 1) – 1(y
– 2) + 2(z
– 1) = 0
![]()
![]() 3x
– y
+ 2z
– 3 = 0. Найдем точку В пересечения прямой
и плоскости (см. задачу 29 пункт 5):
3x
– y
+ 2z
– 3 = 0. Найдем точку В пересечения прямой
и плоскости (см. задачу 29 пункт 5):

Ответ:
![]()
32. Через точку M (3; –1; 0) провести прямую, параллельную двум плоскостям x – y + z – 3 = 0 и x + y + 2z – 3 = 0.
Указание:
Плоскости
![]() x
– y
+ z
– 3 = 0 и
x
– y
+ z
– 3 = 0 и
![]() x
+ y
+ 2z
– 3 = 0 не параллельны, т.к. не выполняется
условие (2.5.1):
x
+ y
+ 2z
– 3 = 0 не параллельны, т.к. не выполняется
условие (2.5.1):
![]() Плоскости
Плоскости![]() пересекаются. Искомая прямаяL,
параллельная плоскостям
пересекаются. Искомая прямаяL,
параллельная плоскостям
![]() параллельна линии пересечения этих
плоскостей. (См. решение задач 24 и 23 пункт
5).
параллельна линии пересечения этих
плоскостей. (См. решение задач 24 и 23 пункт
5).
Ответ:
![]()
33. Составить
уравнение плоскости, проходящей через
две прямые ![]()
![]()
 Указание: 1
способ.
Составим уравнение искомой плоскости
Указание: 1
способ.
Составим уравнение искомой плоскости
![]() по точке
по точке![]() ,
лежащей на прямой
,
лежащей на прямой![]() ,
и нормальному вектору
,
и нормальному вектору![]() .
Вектор
.
Вектор![]() будет равен векторному произведению
направляющих векторов прямых
будет равен векторному произведению
направляющих векторов прямых![]() ,
которые найдем из канонических уравнений
прямых
,
которые найдем из канонических уравнений
прямых![]() (формула 3.1.1):
(формула 3.1.1):
![]() =
(7; 3; 5) и
=
(7; 3; 5) и
![]() =
(5; 5; –3)
=
(5; 5; –3)
![]()

Координаты точки
![]() найдем
из канонических уравнений прямой
найдем
из канонических уравнений прямой
![]()
![]() Составляем уравнение
плоскости
Составляем уравнение
плоскости
![]() по точке
по точке![]() и вектору нормали
и вектору нормали![]() =(–34; 46; 20) (см. пример
1 пункт 2.2)
=(–34; 46; 20) (см. пример
1 пункт 2.2)
![]() 17x
– 23y
– 10z
+ 36 = 0.
17x
– 23y
– 10z
+ 36 = 0.
 2 способ.
Находим направляющие векторы
2 способ.
Находим направляющие векторы
![]() =
(7; 3; 5) и
=
(7; 3; 5) и![]() =
(5; 5; –3) из канонических уравнений прямых
=
(5; 5; –3) из канонических уравнений прямых![]() Точку
Точку![]() (0;
2; –1) находим из уравнения
(0;
2; –1) находим из уравнения![]()
![]() . Возьмем произвольную
точку плоскости
. Возьмем произвольную
точку плоскости
M
( x;
y;
z).
Векторы
![]() –
компланарны, следовательно,
–
компланарны, следовательно,![]()
![]() Из этого условия
получаем уравнение плоскости:
Из этого условия
получаем уравнение плоскости:

Ответ: 17x – 23y – 10z +36 = 0.
34. Составить
уравнение плоскости, проходящей через
точку
![]() (2;
0; 1) и прямую
(2;
0; 1) и прямую![]()
Указание:
Убедимся прежде всего, что точка
![]() на данной прямой не л
на данной прямой не л ежит:
ежит:![]() Точку
Точку![]() и направляющий вектор
и направляющий вектор![]() находим из канонических уравнений
прямой
находим из канонических уравнений
прямой![]() :
:
![]() (1;
–1; –1) и
(1;
–1; –1) и
![]() =
(1; 2; –1). Нормальный вектор искомой
плоскости
=
(1; 2; –1). Нормальный вектор искомой
плоскости
![]() Координаты нормального вектора найдем,
зная координаты
Координаты нормального вектора найдем,
зная координаты![]() =(1; 2; –1) и
=(1; 2; –1) и
![]() =
(1; 1; 2):
=
(1; 1; 2):
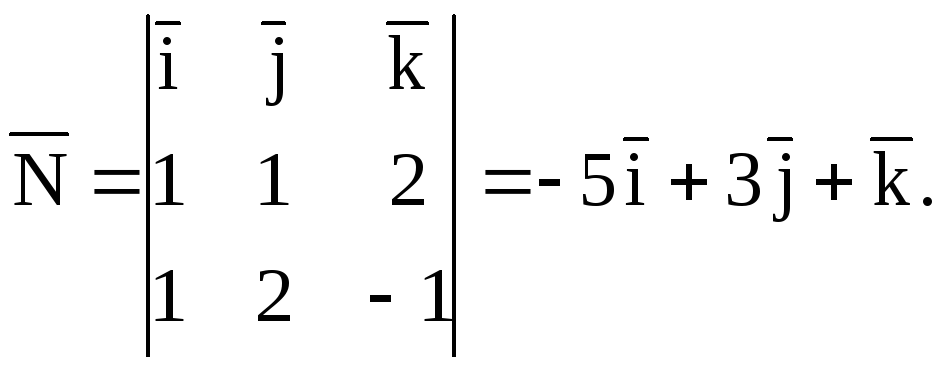
Составляем уравнение
плоскости по точке
![]() (2;
0; 1) и нормальному вектору
(2;
0; 1) и нормальному вектору![]() =
(–5; 3; 1):
=
(–5; 3; 1):
–5(x – 2) + 3(y – 0) + 1(z – 1) = 0.
Ответ: 5x – 3y – z – 9 = 0.
