3. Нахождение экстремума функции нескольких переменных (вариант 8).

Цель работы: изучение метода поиска экстремума нелинейной функции нескольких переменных.

Задание: найти градиентным методом экстремум функции нескольких переменных в соответствии с вариантом задания.

Для нахождения экстремума функции нескольких переменных с помощью градиентного метода необходимо вычислить градиент функции и приравнять его к нулю. Градиент функции равен:

Приравнивая каждую компоненту градиента к нулю, получим систему уравнений. Решая эту систему уравнений, можно найти точки, в которых градиент равен нулю. Эти точки являются кандидатами на экстремумы функции. Для определения типа экстремума (минимум, максимум или седловая точка) необходимо вычислить матрицу Гессе и оценить ее знакоопределенность.

Для решения системы уравнений мы можем использовать метод Гаусса-Жордана. Для этого мы можем записать расширенную матрицу системы уравнений и привести ее к ступенчатому виду. Затем мы можем применить обратный ход метода Гаусса-Жордана, чтобы получить решение системы уравнений.

Расширенная матрица системы уравнений будет выглядеть следующим образом:

[0 4 -1 | 0]

[3 0 -1 | 0]

[-1 0 -2 | 0]

Приведем эту матрицу к ступенчатому виду:

[3 0 -1 | 0]

[0 4 -1 | 0]

[0 0 -2/3 | 0]

Затем мы можем применить обратный ход метода Гаусса-Жордана:

x1 = 0

x2 = 0

x3 = 0

Решая систему уравнений, полученную ранее, мы находим, что x1 = 0, x2 = 0 и x3 = 0. Это означает, что точка (0,0,0) является кандидатом на экстремум.

Чтобы определить тип экстремума, вычислим матрицу Гессе:

Матрица считается отрицательно определенной, если все ее главные миноры имеют знак (-1)^k, где k - порядок минора. Главным минором порядка k матрицы A называется определитель матрицы, составленной из первых k строк и первых k столбцов матрицы A.

В нашем случае главные миноры этой матрицы равны:

∆1=0

∆2=-9

∆3=0

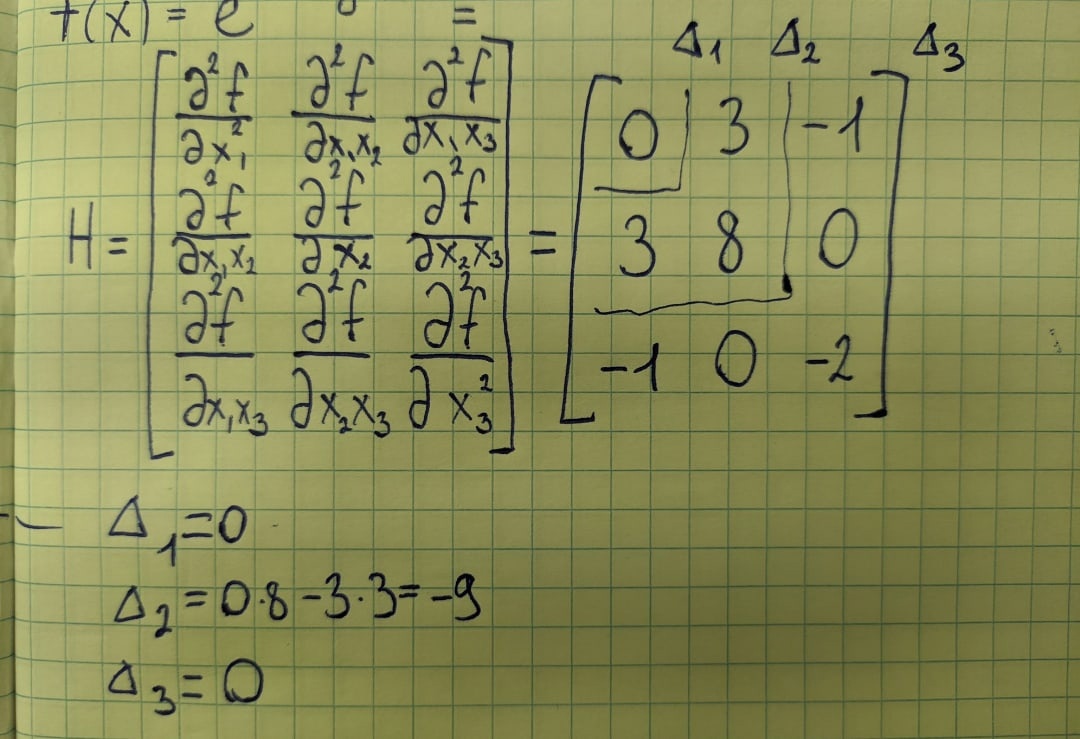
Так как все главные миноры имеют знак (-1)^k, матрица Hf(x) является отрицательно определенной. Это означает, что точка (0,0,0) является максимумом функции f(x).

Ответ: Максимум функции равен f(0,0,0) = 0 и достигается в точке (0,0,0).

4. Нахождение экстремума функции в среде ms Excel (вариант 8)

Цель работы: изучение возможностей среды Excel в связи с задачей оптимизации решения уравнения с учетом наложенных ограничений, приобретение практических навыков решения задач оптимизации в среде Excel

Задание: решить задачу оптимизации в среде Excel для функции с учетом заданных по варианту условий.

Условие задания согласно выбранному варианту:

№ варианта	Функция f(x)	Условие минимизации	Условие максимизации
8	2x­1 + 3x2	2x­1 - x2 < 16	3x­1 + 2x2 = 18

1. Проверить наличие функции аналитического поиска решения на панели быстрого доступа Excel, при необходимости добавить ее в соответствии с описанным порядком действий.

Включил надстройку «Поиск решения» в приложении Microsoft Excel следующим способом:

1. Открыл Microsoft Excel.

2. Нажал Файл > Параметры.

Рисунок 4 – Открытие параметров Excel

3. В открывшемся окне параметров Excel выбрал «Надстройки» > Управление «Надстройки Excel» > Перейти.

Рисунок 5 – Открытие надстроек Excel

4. В открывшемся окне надстроек включил доступную надстройку «Поиск решения» > затем нажал «ОК».

Рисунок 6 – Включение надстройки «Поиск решения»

5. В результате надстройка была включена. Её можно найти в верхней панели Excel > Данные > Анализ > Поиск решения.

Рисунок 7 – Отображение надстройки «Поиск решения»