
книги из ГПНТБ / Иваницкий Г.Р. Исследование микроструктуры объектов методами когерентной оптики
.pdfднями формы объекта. Характер изменения дисперсии
величины р в функции некоторых параметров объекта позволил бы установить предельные значения величины cl, обеспечивающие получение заданной ошибки обнару
жения, а также рассмотреть методы оптимального с точ
ки зрения минимизации величины ексинтеза классов,
р
поскольку мы свободны в выборе способа расчле нения пространства изо бражений объекта па классы.
Необходимо учесть то обстоятельство, что изме ряемая с помощью дву мерных согласованных фильтров функция корре ляции представляет собой результат анализа выбо рок чрезвычайно ограни ченной протяженности, со ответствующих размерам обнаруживаемых объек тов. Поэтому совокуп ность измеренных в ре зультате эксперимента значений корреляционной функции эталона и изо бражения реальной клет ки, представляющей со гласно принятой модели
сумму эталонного изображения и шумовой составляю щей, будет представлять множество случайных величин.
Попытаемся количественно оценить дисперсию оце нок 'Корреляционной функции эталонных изображений и реальных клеток, вычисляемой методами двумерной согласов анной фильтрации.
16. ВЛИЯНИЕ ИЗМЕНЧИВОСТИ ФОРМЫ НА ВЕЛИЧИНУ ДИСПЕРСИИ ОЦЕНОК КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
Под эталонным изображением будем понимать изоб ражение, координаты точек которого являются матема тическим ожиданием координат соответствующих точек
80
контуров реальных элементов объектов обучающей по следовательности, составляющих класс. Распределение плотности объекта представляется в виде аддитивного сочетания эталонного изображения и шумовой состав ляющей.
На каждой из пространственных несущих согласован ного фильтра фиксируется спектр соответствующего эта лонного изображения. Вся совокупность изображений, составляющих класс, представляет собой последователь ность выборок, для которой в результате фильтрации вычисляются значения корреляционной функции эталон ного изображения и элементов реальных -клеток.
Вследствие конечной протяженности каждой из выбо рок [в предположении стационарности шумового процес са [ш(х, у)1] оценки корреляционной функции эталонного изображения и совокупности реальных объектов одного класса образуют ансамбль случайных величин. Мера рассеяния оценок взаимной корреляционной функции эталонного изображения и выборочных изображений, со ставляющих класс, определяется величиной дисперсии полученной совокупности оценок. Цель данного парагра фа состоит в том, чтобы представить значение дисперсии оценок корреляционной функции через статистические параметры шумового процесса с учетом характеристик используемой оптической системы. Это позволит по до пустимому отклонению отношения сигнал/шум оценить предельные значения величины дисперсии шумового про цесса для совокупности объектов, составляющих класс
[Л. 39].
Полагая, что общие соображения, касающиеся сред неквадратичного значения флюктуаций при многократ ном измерении среднего на конечном интервале [Л. 19], остаются в силе при рассмотрении стационарных функ ций двух переменных и учитывая, что функция взаимной корреляции является результатом осреднения произведе ния двух случайных функций конечной протяженности (эталона и реальной выборки), определим величину дисперсии оценок корреляционной функции.
По определению
o2r= C R 4 A x ', Ay ' ) > - < R ( A x ' , Ду’) > \ (140)
где R( Ад/, Ау') — функция взаимной корреляции эталон ного изображения и совокупности эталонного изображе ния и шума. Символ < > означает осреднение по множе-
6— |
552 |
81 |
ству. В свою очередь R(Ax', |
Ау') |
является |
результатом |
|||
осреднения |
по |
переменным |
произведения |
faT(x', |
у') X |
|
Х[/эт(Д', у) +fui(x, у)] |
|
|
|
|
||
R(Ax', |
Ay') = M {fm(x' y')\fm{x, |
у) +!ш(х, у)]}. |
(141) |
|||
Обозначим f3T{x, у)[}эт{х, у)+1ш{х, у)] 'через z(x, у). |
||||||
Тогда |
|
|
|
|
|
|
4 |
= < |
М2 [г (х, у)J> |
- < |
М [г (х, у)| > 2, |
(142) |
|
где уменьшаемое есть момент второго порядка функции 2 (х, у), а вычитаемое — квадрат момента .первого поряд ка той же функции. -Поменяв местами осреднения по множеству и по переменным, получим:
<Л1[г(л-, //)]> = М < г ( . г , у )> . |
(143) |
|
Поскольку рассматриваемые |
случайные |
процессы |
предполагаются стационарными, |
то |
|
М < 2 (х, у ) > = < г ( х , у)>.
Момент второго порядка равен:
<ЛН[2 (л-, |
у)]> = <М [г(х, y,)z(x', у')]>. |
(144) |
Таким образом: |
|
|
з1 = < М [ г ( х , y)z(x', t/')]> — < z ( x , у) > 2. |
(145) |
|
Развернем выражение (145) |
|
|
4 — |
У)2 (х '’ у') dx dy dx'dy' > — |
|
|
— < z { x , y ) > 3, |
(146) |
где 5 — область, |
анализируемая во входной плос-кости |
|
коррелятора. Протяженность этой области ограничена апертурой используемой линзы и ма-ксимальньши углами дифракции, обусловленными спектральным составом изображения. Предполагая, что эта область имеет фор му прямоугольника, и обозначив протяженность ее в на правлениях х и у соответственно через Ьх и Lv, можно записать:
у— I — L
ьх LV
L X
— <z(JC, у) > 2] dxdy j
82
После промежуточных преобразовании, положив
<г(х, y)z(x', |
y ')> = R,(Ах, |
Ay), |
|
где Ах = х'—х, Ау = у'— у, |
можно |
прийти |
к выражению |
2Lх 2L |
|
|
|
° J = z i r J |
j1 |
A y ) - |
|
оо
- < г ( х , |
(148) |
Несложно показать [Л. 39], что предполагая отсутст вие корреляции в распределениях плотностей эталона и шума, (148) можно представить в виде
2I.x 21у
4 = 1 ^ 7 ( f Яш (А-v. ДУ) ( 1 - ^ - ) ( 1 - 2 1 7 ) dAx
оо
(149)
где Е — энергия эталонной функции; Rm(Ax, Ay) — функ ция корреляции шума.
Таким образом, дисперсия оценок корреляционной функции зависит от протяженности анализируемых вы
борок и функции |
корре |
|
|
|
|
|
|||||
ляции шума. |
|
величина |
|
|
|
|
|
||||
Предельная |
|
|
|
|
|
||||||
Lx, определяющая |
грани |
|
|
|
|
|
|||||
цы |
существования |
вход |
|
|
|
|
|
||||
ного |
распределения |
(в |
|
|
|
|
|
||||
направлении |
х, |
рис. |
14) |
|
|
|
|
|
|||
в общем случае ограниче |
|
|
|
|
|
||||||
на |
параметрами оптиче |
|
|
|
|
|
|||||
ской системы и частотным |
|
|
|
|
|
||||||
составом |
изображения |
|
|
|
|
|
|||||
(выражение для Ьу иден |
F hc. 14. |
Соотношение |
между |
про |
|||||||
тично) |
|
|
|
|
тяженностью |
входного распреде |
|||||
|
|
|
|
ления, |
максимальным |
углом |
ди |
||||
Lx^ A —2FtgQ, |
(ISO) |
||||||||||
фракции |
и апертурой |
системы |
|||||||||
где |
А — диаметр |
|
линзы; |
LX^ A — 2F |
— - 1 |
|
|
||||
Л — ее фокусное |
расстоя- |
|
|
> 4тс2 — А2о)- |
|
||||||
ине; |
0 — максимальный |
|
|
|
|
|
|||||
угол дифракции, соответствующий наивысшей простран
ственной^ частоте, пропускаемой |
системой при |
данном |
Lx. В свою очередь sin 0=A co/2jt, |
где К — длина |
волны |
g* |
|
83 |
используемого освещения; со — пространственная |
ча- |
||||
стота. |
|
|
|
|
|
Таким образом: |
jA |
|
|
|
|
Lx< |
V-№ — l-w- |
2F. |
(151) |
||
2 F |
|||||
Отношение Aj2F имеет смысл относительной апер- |
|||||
туры системы. Очевидно, что при |
|
|
|||
|
_Л |
Хсо |
|
|
|
|
21- > Y 4я2 -- Л2С02 |
|
|
||
оптическая система не ограничивает полосы частот вход ного распределения. Предельное значение угла дифрак ции, еще не ограничиваемого оптической системой, удов
летворяет соотношению |
|
|
|
А _ |
Хсо |
(152) |
|
IgO = - F |
Y - I tz2 — \ 2ы 2 |
||
|
|||
При этом входное распределение стягивается в точку. |
|||
Дальнейшее уменьшение |
отношения A/2F приводит |
||
к сокращению полосы частот входа. |
|
||
Анализ статистических характеристик шумовых со ставляющих изображений объекта показал, что коэффи циент корреляции гш(Дх) = /?ш(Дх)/а2ш достаточно хоро
шо аппроксимируется функцией вида |
|
||
|
Гш(А.т) =ехр[— а|Ах|]. |
(153) |
|
Подставив выражение для коэффициента корреляции |
|||
в (149) и рассматривая |
случай одной переменной, |
окон |
|
чательно получим: |
|
|
|
|
2 |
|
|
= |
~TL | ( 1 ~ |
ехР (— а I Аа' I ) dhx = |
|
= |
-Щ - |
i l1exp ( - 2*LX)]}. |
(154) |
Коэффициент затухания корреляционной функции а является величиной, обратно пропорциональной интер
валу корреляции Дхкор, |
который в свою очередь связан |
||
с полосой частот шумового процесса |
соотношением |
||
&хКОр = 2п/А(ох. Поэтому |
выражение (154) |
можно |
пере |
писать так: |
|
|
|
2 |
А<Дд-L н |
(155) |
|
gr |
71 |
. |
|
|
|
||
84 |
|
|
|
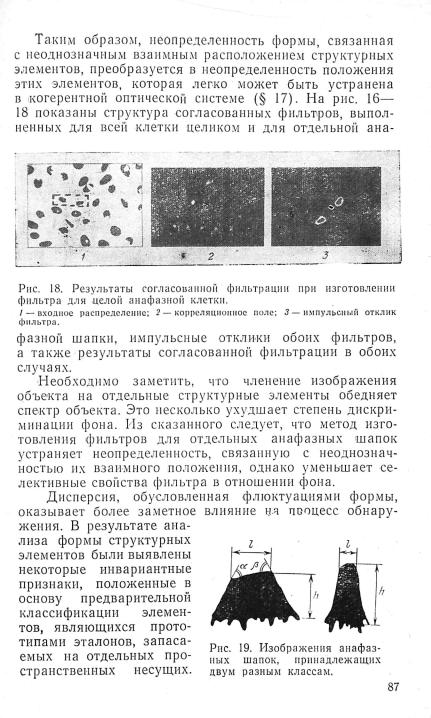
Характер |
изменения |
ди |
|
|||||
сперсии в функции произве |
(8т/см2-ср)2 |
|||||||
дения |
Au>xLx |
показан |
на |
|
||||
рис. 15. Анализ зависимости |
|
|||||||
ozR=f(AioxLx) |
показывает, |
|
||||||
что при заданной протяжен |
|
|||||||
ности |
объекта |
во |
входной |
|
||||
плоскости наибольшее укло |
|
|||||||
нение оценок функции кор |
|
|||||||
реляции |
наблюдаются |
для |
|
|||||
низкочастотных |
составляю |
|
||||||
щих |
шумовых |
компонентов |
|
|||||
изображений объекта, т. е. |
|
|||||||
для сильнокоррелированных |
Рис. 15. График изменения ди |
|||||||
изменений формы |
объекта. |
сперсии оценок корреляцион |
||||||
ной функции в зависимости от |
||||||||
Расширение |
полосы частот, |
|||||||
произведения 'Дм.*/.*. |
||||||||
занимаемой |
шумовыми |
со |
|
|||||
ставляющими, вызывает уменьшение дисперсии по зако ну рис. 15. Полагая, что величина ошибки не может быть больше некоторой заданной величины, можно опре делить значение допустимой дисперсии в пределах класса.
Полученные выводы могут быть также использованы для оптимального с точки зрения минимизации диспер сии оценок корреляционной функции синтеза эталонов.
Например, в структуре анафазных шапок (анафазная стадия деления клетки обычно используется для ис следования хромосомных повреждений) медленные, сильнокоррелированные изменения формы, как правило, связаны с участками, обращенными к центру митотиче ского аппарата и образованными центромерами хромо сом, движущимися вдоль нитей веретена. Такого же рода изменения наблюдаются на боковых сторонах шап ки. Быстрые, слабокоррелированные изменения формы чаще всего связаны с областями, формируемыми хроматндными нитями. Поэтому для обеспечения минималь ной дисперсии оценок корреляционной функции в осно ву классификации целесообразно положить признаки, определяющие устойчивость сильно коррелированных изменений в пределах класса. Другими словами, форми рование классов нужно производить таким образом, чтобы в пределах класса сохранялось максимальное по добие элементов, связанных с сильнокоррелированными изменениями формы. Эталоны, синтезированные для фор-
85
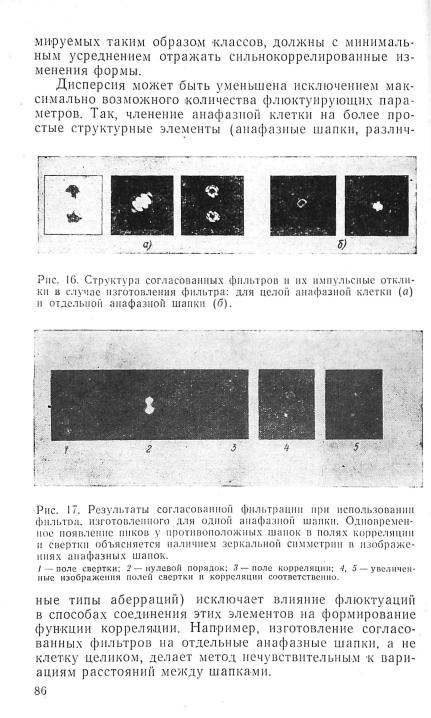
В качестве таких признаков при 'классификации формы анафазных шапок были использованы следующие приз наки (рис. 19): 1) площадь; 2) протяженность стороны шапки, обращенной в сторону полюса 'митотического ап парата и образованной центромерами хромосом, движу щимися вдоль нитей веретена; 3) углы, образованные стороной, обращенной к полюсу, н боковыми сторонами; 4) отношение высоты шапки к ее ширине (на уровне половины высоты); 5) характер «бахромы», образован ной хроматидами. Классификация по указанным приз накам позволила выявить устойчивые формы, доста точно распространенные в исследуемой популяции клеток.
Однако с точки зрения проведенного анализа диспер сия оценок корреляционной функции может быть умень шена, а границы класса несколько расширены, если в пределах класса сохранять в первую очередь устойчи вость сильнокоррелированных изменений формы.
Представляет интерес исследование вопроса о харак тере изменения дисперсии оценок корреляционной функ ции за счет флюктуаций формы при регулировке дискри минирующих свойств фильтра.
Целесообразность такого рода преобразований ста новится очевидной, если иметь в виду, -что этот путь по зволяет наиболее рационально использовать информаци онную емкость двумерного согласованного фильтра. Как правило, подобная операция осуществляется изменением коэффициента передачи оптической системы для двумер ной согласованной фильтрации. Так, уменьшение селек тивных свойств фильтра может быть осуществлено вве дением пространственного интегрирования (коэффици ент передачи системы уменьшается при этом обратно пропорционально пространственным частотам со* и соу) или просто блокированием верхних пространственных частот. Последнее эквивалентно введению в тракт фильт ра -низких пространственных частот. Обратная операция, имеющая целью увеличить селективные свойства фильт ра, сводится к ослаблению удельного веса низких про странственных частот. Она может быть выполнена вве дением в оптическую систему дополнительного фильтра верхних пространственных частот или осуществлению пространственного дифференцирования.
Сигнал на выходе такой системы можно представить в виде свертки аппаратной функции системы и входной реализации
88
со
я * (АХ. A|/) = J J h ( x - x ' , y - y ' ) f BK( x ’ , y ' ) d x ’ d y'. (156)
—00
При этом аппаратная функция представляет произведение аппа ратной функции согласованного фильтра и аппаратной функции дополнительного фильтра
Л(х, у) = lic .ty[х, |
</)Лд.ф'(*- У)- |
(‘157) |
. Можно показать, что дисперсия |
оценок корреляционной |
функции |
с учетом дополнительного фильтра определяется выражением [Л . 40]
00
|
|
|
° к = |
|
л®ня(д*. *у)~ |
|
|
|||
|
|
|
—00 |
|
|
|
|
|
|
|
|
|
— |
< f n x ( x ', |
y ' ) f э т (х ', |
у ') |
> |
2] d h x dAy, |
(158) |
||
где Rn(Ax, A y ) — |
автокорреляционная |
функция аппаратной |
функции |
|||||||
системы; |
R(Ax, |
Ay) — |
корреляционная |
|
функция |
произведения |
||||
[fn x]*, у) fat (.v, (/)], т. е. |
если |
дисперсия |
оценок |
корреляционной |
||||||
функции при неограниченной полосе частот оптической |
системы |
|||||||||
определяется |
корреляционной |
функцией |
произведения |
у) X |
||||||
Х 1ат{х, |
(/)] |
[выражение |
(148)], то при |
введении дополнительного |
||||||
фильтра она описывается интегральным выражением типа свертки (158). В этом выражении в качестве одной из свертываемых функ ций используется автокорреляция аппаратной функции системы, а вторая свертываемая функция пропорциональна функции корре ляции произведения входного и эталонного распределений.
Рассмотрим более детально каждый из сомножителей в урав нении (158). В предположении независимости распределений плот ности эталона и шума корреляционная функция произведения вход ного и эталонного распределений R(<Ах, А у) определяется корреля ционной функцией шума.
Величина < f Bx'(x, y ) f B?(x, у ) > 2 эквивалентна энергии эталонной функции.
В ряде случаев полоса пространственных частот системы огра ничена апертурой используемых линз или специально вводимыми
вспектральную плоскость диафрагмами.
Вкачестве примера ниже рассмотрена автокорреляция аппа ратной функции оптической системы при изотропном ограничении
полосы пространственных частот.
Коэффициент передачи такого фильтра нижних частот описы
вается выражением |
|
|
|
|
|
Н |
(со*, |
сон) = g | при |
со2, + со2 | ^ |
\ |
(158а) |
где а — радиус |
зоны |
прозрачности |
в частотной |
плоскости. |
|
В этом случае зона прозрачности представляет собой функцию— круг. Поэтому аппаратная функция подобной системы определяется преобразованием Фурье от функции, описываемой выражением (158а). Как известно [Л . 50], преобразование Фурье такой функции определяется как
£ ( Р ) = ^ Д |
(159) |
89
