11. Оптимизация транспортных процессов точным методом

После построения опорного плана переходят ко второму этапу реше­ния транспортной задачи. Здесь производится последовательное улучшение опорного (начального) плана. В настоящее время существует много мето­дов последовательного улучшения опорного (начального) плана. К наиболее употребительным методам относятся распределительный метод, метод потенциалов, метод steррing - stопе и ряд других. Основой вычислительного процесса (алгоритма) этих методов является определение критерия опти­мальности

где: Сij - затраты на доставку изделия из i-го пункта производства (ремонта, обслуживания) в j-ый пункт использования (эксплуатации);

Zij — расчетные затраты на доставку изделия из i-го пункта производ­ства (ремонта, обслуживания) j-ый пункт использования (эксплуатации), определяемые для тех клеток опорного плана, в которые не распределены объемы работ.

Если все 0, то данный опорный план оптимальный, если нет, то с помощью этого критерия оптимальности можно указать способ улучшения этого плана.

Ограничимся рассмотрением метода потенциалов. Метод потенциалов включает следующие основные этапы:

1. Составление и решение системы уравнений с переменными Vi ,Ui которые удовлетворяют такой системе равенств

Vj-Ui =Cij, (C = 1,2,...,т), (j =1,2,...,n).

При этом используются переменные и затраты с теми индексами i и j, на пересечении которых в соответствующих клетках распределены объемы работ. Для нашей задачи система уравнений будет (см. табл. 5.7) такая:

V₃-U₁=С₁₃=24,

V₂-U₂=С₂₂ = 18,

V₁-U₃=С_3]=19,

V₂-U₃=C₃₂ =10,

V₁-U₄= C₄₁, =3,

V₃-U₃ = C₃₃ =100,

V₄-U₄ = C₄₄ =8,

Имеем 7 уравнений и 8 неизвестных, поэтому одному из неизвестных, желательно наиболее часто встречающемуся в уравнениях, дается произ­вольное значение, как правило, для облегчения счета, равное нулю. В на­шей системе уравнений наиболее часто встречающееся неизвестное — это U₃. Положим U₃ ⁼ 0.

Решая последовательно соответствующие уравнения, получим

V₁ = 19, V₂= 10, V₃= 100, U₁= 76, U₂= - 8, U₄ = 16, V₄ = 24.

2. Определение расчетных значений Z_ij = V_i — U_i,. При этом использу­ются те индексы I и j, на пересечении которых в соответствующих клетках не распределены объемы работ:

Z₁₁ =V₁-U₁ =19-76 = -57,

Z₁₂ =V₂-U₁ =10-76 = -66,

Z₁₄ =V₄-U₁ = 24 - 76 = -52,

Z₂₁ =V₁-U₂ =19 + 8 = 27,

Z₂₃ =V₁-U₂ =100 + 8 = 108,

Z₂₄ =V₄-U₂ =24 + 8 = 32,

Z₃₄ =V₄-U₃ =24 + 0 = 24,

Z₄₂ =V₂-U₄ =10-16 = -6,

Z₄₃ =V₃-U₄ =100-16 = 84.

3. Определение значений критерия оптимизации, ипро­верка условия оптимальности, если все О, то исходный план оптима­лен. Если некоторые 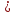О, то переходят к новому опорному плану:

=38 + 66 = 104,

=92 + 52 = 144,

=58-27 = 31,

= 56 -108 = -52,

=72-32 = 40,

=30-24 = 6,

= 36 + 6 = 42,

В нашем случае — переходим к новому опорному плану.

4. Построение нового опорного плана, которому отвечает меньшее значение целевой функции. Для этого в опорный план вводится та переменная Xij, которой отвечает наименьшее отрицательное значение . Вводя новую переменную, одновременно изменяют другие переменные, по меньшей мере, в трех заполненных клетках (чтобы не нарушались итого­вые величины в строках и столбцах таблицы a_i и b_i)- Для этого строят мно­гоугольник, в котором одна из вершин находится в свободной клетке, для которой 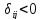и имеет наименьшее значение, а остальные — в запол­ненных объемами работ (загружены); при этом все углы многоуголь­ника должны быть прямыми (в нашем примере свободная клетка А2В3табл. 5.7). В пределах клеток, лежащих в вершинах многоугольника (рис. 5.1, а), производят перераспределение объемов работ.

Рис. 5.1. Перераспределяемые (а) и перераспределенные объемы работ (б)

Если для свободной клетки поставить знак " + ", а в следующей вершине " - ", затем " + " и т. д., поочередно изменяя знак, то в свободную клетку пере­носится меньшее из чисел, стоящих в клетках с отрицательными знаками. В результате она исключается из опорного базиса как базисная переменная. Од­новременно необходимо установить равновесие по всему многоугольнику.

Используя правило перераспределения объемов работ в пределах мно­гоугольника, проводим распределение объемов работ (рис. 5.1, б). При этом сумма объемов работ по всем строкам и по всем столбцам должна оста­ваться без изменения.

В нашем примере многоугольник имеет очень простой вид. На практи­ке при решении задач большой размерности многоугольник может прини­мать самые замысловатые виды, образуя множество пересекающихся ли­ний. Проводя соответствующие изменения в исходном опорном плане, окончательно получим новый опорный план (табл. 5.8).

ДСК Аi	Микрорайоны Bi					Производственная Мощность ДСК аi
	B1	B2	B3	B4
	Затраты на доставку изделия Сij из Аi пункта Производства в Bi пункт использования
A1	70	38	24 14	92	14
A2	58	18 19	56 1	72	20
A3	19 23	10 3	100	30 4	26
A4	3 7	36	121	8 34	41
Годовой Объем Работ Vi	30	22	15	34	-

Суммарные затраты на транспортировку всех изделий составят У= 14-24+ 19-18+ 1-56 + 23-19 + 3-10 + 7-3 + 34-8 = 1494руб

.

Это значительно меньше, чем при исходном опорном плане, опреде­ленном способом аппроксимации Фогеля.

По сравнению с исходным опорным планом, который представляется на первый взгляд также весьма разумным, суммарные затраты на доставку всех изделий уменьшились примерно на 3,3 %.

Нахождением нового опорного плана заканчивается первое приближе­ние (первая итерация). Дальше аналогичные операции повторяются, но уже для нового опорного плана.

Последующие вычисления показывают, что все , т. е. опорный план, полученный втабл. 5.8, является оптимальным.

Часто при построении опорного плана или в процессе решения задачи методом потенциалов число клеток, в которые распределены объемы работ, меньше т+п-1, где т - число производителей изделий (строк), п — число потребителей изготовленных изделий (столбцов). В этой ситуации говорят, что имеет место случай вырождения. Для устранения вырождения приме­няют два способа:

вводят в некоторые свободные клетки изделия, число которых равно нулю, и данные клетки считают занятыми;

выбирают несколько клеток, дополняющих сумму занятых клеток до т+п-1, и вводят в них сколь угодно малое число изделий.