§7. Вычисление предела функции в точке
Наиболее универсальным средством
вычисления предела функции f(x)
в точке a является замена
переменной:
.
В результате необходимо вычислить
предел функции f(t+a)
при t→0. При этом можно
воспользоваться таблицей эквивалентных
функций, см. §4. Обратим внимание, замена
t=x–a
устроена таким образом, что при x→a–0
t→–0 и вычисляется предел
в точке t=0 слева, при x→a+0
t→+0 – вычисляется предел
в точке t=0 справа.
Пример.6.
Вычислить предел
.
◄
.
Подставляем значение x=0
в функцию f(x).
Выясняется, что точка x=0
не принадлежит области определения
функции f(x)
(деление на нуль), неопределенность вида
,
вычислить можно только предельное
значение функции f(x)
при x→0.
x→0, замена переменной не
требуется. Аргумент функции ln(1+5x),
(5x) и аргумент функции
sin2x, (2x)
– бесконечно малые величины, (§5),
,
,(9
и 1 §4).
.
Были использованы свойствами предела
(§2).
Ответ:
.
Пример.7.
Вычислить предел
.
◄
.
Подставляем значение x=0
в функцию f(x).
Выясняется, что точка x=0
не принадлежит области определения
функции f(x)
(деление на нуль), неопределенность вида
,
вычислить можно только предельное
значение функции f(x)
при x→0.
x→0, замена переменной не
требуется. Аргумент функции cos4x,
(4x) и аргумент функции
tg3x, (3x)
– бесконечно малые величины, (§5),
,
,(2
и 3 §4).
Используем формулу
,
3x→0, (9 §4).
Мы воспользовались свойствами предела
(§2) и непрерывностью функций x
и (
)
в точке x=0 (§6). Ответ:
.
Пример.8.
Вычислить предел
.
◄
.
Функция f(x)
непрерывна в точке x=–1,
.
Ответ:
.
Пример.9.
Вычислить предел
.
◄
.
Введем новую переменную t=x–(–1)=x+1,
при x→–1 t→0,
x=t–1.
Ответ:
.
Пример.10.
Вычислить предел
.
◄
.
Введем новую переменную t=x–π,
t→0, x=t+π.
.
Ответ:
.
§7. Вычисление предела функции при X→∞
Наиболее универсальным средством
вычисления предела функции f(x)
при x→∞ является замена
переменной:
.
В результате необходимо вычислить
предел функции f(1/t)
при t→0. При этом можно
воспользоваться таблицей эквивалентных
функций, см. §4. Обратим внимание, замена
t=1/x устроена
таким образом, что при x→–∞
t→–0 и вычисляется предел
в точке t=0 слева, при x→+∞
t→+0 и вычисляется предел
в точке t=0 справа. Замети,
что практическое применение замены
t=1/x приводит
к трудоемким преобразованиям исходного
вида функции f(x)
в функцию f(1/t).
Поэтому в практике расчетов замену
t=1/x явно не
проводят. Функцию f(x)
преобразуют таким образом, чтобы
бесконечно большая переменная x
менялась на обратную к ней бесконечно
малую переменную 1/x,
которая используется при вычислении
предела функции.
Пример.11.
Вычислить предел
.
◄
.
Выносим максимальные степени n
под корнями, в числителе и знаменателе
дроби. Получим
.
Ответ:
.
Пример.12.
Вычислить предел
.
◄ Неопределенность вида
.
Выносим бесконечно большую величину x
под корнем.
Ответ:
.
Пример.13.
Вычислить предел
.
◄ Неопределенность вида
.
Ответ:
.
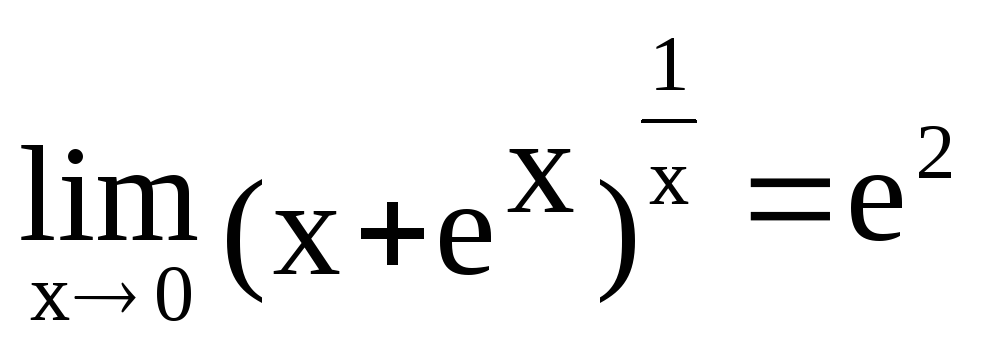Пример.14.
Вычислить предел
.
◄ Неопределенность вида
.
Ответ:
.