24
вращений, происходящих внутри этого интервала температур.
При отсутствии полиморфных и агрегатных превращений энтропия вещества определяется соотношением:
= T C dT S ∫ P
0 T
С учётом полиморфных и агрегатных превращений энтро- пия определяется из выражения:
Tпер СαdT |
|
∆Hпер |
|
T |
СβdT |
|
||
S = ∫ |
P |
+ |
|
+ |
∫ |
P |
. |
|
Тпер |
||||||||
0 |
T |
|
|
T |
T |
|
||
|
|
|
|
|
пер |
|
|
|
1.9. Характеристические (термодинамические) функции
Характеристической функцией называется такая функция, по- средством которой или ее производной могут быть выражены в явной форме термодинамические свойства системы. Под термоди-
намическими свойствами понимают такие физические свойства, кото- рые зависят только от температуры, давления (или объёма) и состава.
Наиболее часто в термодинамике используют следующие характеристические функции: внутренняя энергия (U), эн- тальпия (H), энтропия (S), изохорно-изотермический потен- циал (F) и изобарно-изотермический потенциал (G).
1.9.1. Изохорно-изотермический потенциал или свободная энергия Гельмгольца (F)
Свободная энергия Гельмгольца (F) является характеристиче- ской функцией при независимых переменных V и T и записывает- ся следующим образом:
dF = −P dV −S dT |
(1.37) |
Полныйдифференциалтакойфункциизаписываетсяследующим образом:
|
∂F |
|
∂F |
|
|
|
dF = |
|
|
dV + |
|
dT . |
(1.38) |
|
||||||
|
∂V T |
|
∂T V |
|
|
|
Запишем объединённое уравнение первого и второго закона термодинамики:
δQ = dU + δA ,
25
δQ = T dS.
Тогда объединённое уравнение будет иметь вид:
dU + δA = T dS, |
(1.39) |
где δA есть элементарная работа термодинамического процесса. Интегрируя выражение (1.39) при V = const и T = const получим рабо-
ту изохорно-изотермического процесса:
AV,T |
= T(S2 − S1) −(U2 − U1) или |
AV,T = (U1 − T S1) −(U2 − T S1), |
(1.40) |
где |
F = U − T S (см. уравнение (1.32)). |
|
|
Тогда: |
|
|
|
|
AV,T = F1 − F2 = −∆F . |
(1.41) |
|
Из выражения (1.41) следует, |
что работа системы при V = const и |
||
T = const равна убыли функции свободной энергии Гельмгольца в дан- ном процессе.
Из (1.41) также следует, что изохорно-изотермических процессах в работу не может перейти вся внутренняя энергия (U). В работу превра- щается только часть её, которая остается после вычета связанной энер- гии. TS — связанная энергия, которая не может быть превращена в ра- боту, и, чем больше энтропия S, тем больше связанная энергия системы.
Продифференцируем выражение (1.32):
dF = dU − T dS − S dT |
(1.42) |
и в (1.42) вместо dU подставим его значение из (1.39), тогда получим:
dF = T dS − P dV − T dS − S dT,
или
dF = −P dV −S dT . |
(1.43) |
||
Тогда в соответствии с (1.38) и (1.43) находим: |
|
||
|
(∂F) |
= −P , |
(1.44) |
|
|
||
(∂V)T |
|
||
26
|
|
|
|
|
(∂F) |
= −S . |
|
|
|
|
|
|
(1.45) |
|
|
|
|
|
|
(∂T)V |
|
|
|
|
|
|
|
|
|
|
|
∂F |
= −P |
|
∂F |
= −S |
Таким |
образом, |
давление |
|||||
|
|
|
|
|
является мерой убыли свобод- |
|||||||||
|
|
∂V T |
|
|
∂T V |
|
|
|||||||
F |
∂2F = − |
∂P > 0 |
F |
|
|
|
ной энергии Гельмгольца с уве- |
|||||||
|
|
|
личением объёма при T = const |
|||||||||||
|
∂V2 |
∂V |
V = const |
|
(1.44), |
а |
энтропия — |
мерой |
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
убыли |
свободной |
энергии |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Гельмгольца |
с |
увеличением |
||||
|
T = const |
∂2F |
∂S |
|
температуры |
при |
V = const |
|||||||
|
|
|
|
|
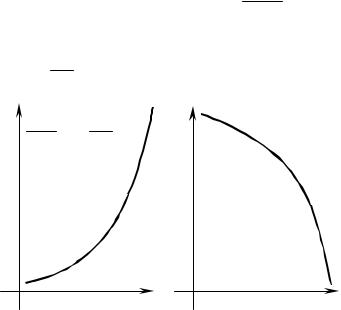
(1.45). |
На |
рис. 1.2 |
это |
пред- |
|||||
|
|
|
|
∂T2 = − |
∂T |
< 0 |
||||||||
|
|
|
|
ставлено графически. |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
V |
|
|
|
T |
1.9.2. Внутренняя энергия |
||||||
|
Рис. 1.2. Графическое представление |
|||||||||||||
|
|
|
|
системы (U) |
|
|||||||||
|
|
зависимостей (1.44) и(1.45) |
|
Объединённое уравнение |
||||||||||
|
|
|
|
|
|
|
|
|||||||
первого и второго законов термодинамики (1.39) в другом |
||||||||||||||
виде можно записать следующим образом: |
|
|
|
|
|
|||||||||
dU = T dS − P dV . |
(1.46) |
Из (1.46) cледует, что внутренняя энергия является характе- ристической функцией при независимых переменных S и V и записывается следующим образом:
U = f(S,V) |
(1.47) |
Запишем полный дифференциал этой функции:
|
∂U |
|
∂U |
dS, |
dU = |
|
dV + |
|
|
|
∂V S |
|
∂S V |
|
сравнивая выражения (1.46) и (1.48), видим, что
∂U |
= −P , |
|
|
|
|
|
∂V S |
|
|
∂U |
= T , |
|
|
|
|
∂S V |
|
(1.48)
(1.49)
(1.50)
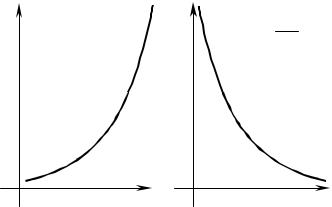
Из (1.49) и (1.50) следует, что давление является мерой убыли внутренней энергии при S = const , а температура — ме- рой возрастания внутренней энергии с увеличением энтропии при V = const . Cказанное графи- чески представлено на рис. 1.3.
1.9.3. Энтальпия системы (H)
Выражение для энтальпии термодинамической системы (1.7) после дифференцирования запи- сывается следующим образом:
|
|
∂U |
= T |
|
|
|
|
U |
|
∂S V |
|
∂2U2 = ∂T |
> 0 |
||
|
∂S |
∂S |
|
|
V = const |
|
|
|
|
|
S |
|
|
|
|
|
27 |
|
|
∂U |
= −P |
||
|
|
|
|
||
U |
|
∂V S |
|
|
|
∂2U |
= − |
∂P |
> 0 |
||
|
∂V2 |
∂V |
|||
|
|
|
|||
|
|
|
S = const |
||
|
|
|
|
|
V |
Рис. 1.3. Графическое представление зависимостей (1.50) и (1.49)
dH = dU + P dV + V dP . |
(1.51) |
Из объединённого уравнение первого и второго закона тер- модинамики определим dU :
dU = T dS − P dV . |
(1.52) |
В уравнение (1.51) вместо dU подставим его значение из (1.46), тогда получим:
dH = T dS − P dV + P dV + V dP, |
(1.53) |
или
dH = T dS + V dP .
Из(1.54) следует, чтоэнтальпияестьфункциядвухпеременных S и
H = f (S,P).
Запишем полный дифференциал этой функции
|
∂H |
|
∂H |
dP ; |
dH = |
|
dS + |
|
|
|
∂S P |
|
∂P S |
|
сравнивая уравнения (1.54) и (1.56), видим, что
|
∂H |
= T , |
|
|
|
|
∂S P |
|
(1.54) P , т. е. (1.55)
(1.56)
(1.57)