Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный медицинский университет им. М. Горького

Предмет:

Физическая химия

Файл:

12_100229_1_69912.pdf

Скачиваний:

355

Добавлен:

23.02.2015

Размер:

2.44 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3311 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Если парциальные давления всех участников химической реакции в исходной неравновесной смеси равны pi = 1 атм., то из (1.110) следует, что

∆G0T = −RT lnKP ,						(1.112)
или из (1.112)
	−∆G0T		−∆H0T		∆S
KP = e	RT = e		RT e R ,
где G0T — стандартный изобарно-изотермический потенциал хими-
ческой реакции при выбранной температуре.
Заменив в (1.110) −RT lnKP на G0T		получим:
∆G = G0 + RT ln				pc	pd	,
∆G = G0 + RT ln				C D		,
	T			paA	pBb
или
∆G = ∆G0T + ∆GP .						(1.113)

Из (1.113) следует, что изменение изобарно-изотермического потенци- ала химической реакции состоит из двух частей. Первая часть ∆G0 — из- менение для реакции, в которой как реагирующие вещества, так и про- дукты реакции, взяты в стандартном состоянии. Для реакции (1.100) ∆G0 есть величина постоянная при T = const и P = const, зависящая только от природы реагирующих веществ. Вторая часть в (1.113) устанавливает за- висимость ∆G химической реакции от состава реакционной смеси. Она представляет собой увеличение изобарно-изотермического потенциала, которое получается при переходе реагирующих веществ, взятых при про- извольно выбранных парциальных давлениях (или концентрациях), в про- дукты реакции, также взятых при произвольно выбранных давлениях.

1.11.2. Уравнения изобары химической реакции

Химическое равновесие есть динамический процесс, и оно смещает- ся в ту или другую сторону при изменения внешних воздействий. На по-

ложение химического равновесия, а, значит, и на константу равновесия значительное влияние оказывает температура.

Зависимость константы химического равновесия от температуры при P = const получим, исходя из изотермы химической реакции (1.110) и уравнения Гиббса-Гельмгольца (1.74):

	∂∆G	,	(1.114)
∆G = ∆H + T		,	(1.114)
	∂T P

Продифференцируем уравнение (1.110) по температуре, учитывая, что парциальные давления pC, pD, pA, pB и, следовательно, от температу- ры не зависят. Тогда

∂∆G			pc	pd	dlnK	P
∂T		= R ln	Ca	Db − R lnKP − RT			.
					dT
	P		pA	pB

В (1.114) подставим результат дифференцирования (1.110) и получим:

∆G = ∆H + RT ln pCc pDd

− RT lnK

− RT2

dlnKP

(1.115)

paA pBb

Далее, приравняем (1.110) и (1.115)

RT ln pCc pDd − RT lnK

= ∆H + RT ln pCc

pDd

− RT lnK

− RT2

dlnKP

paA pBb

Из последнего уравнения следует, что:

dlnKP	=	∆H	.	(1.116)
dT
		RT2

Уравнение (1.116) получило название изобары химической реакции.

Для расчётов равновесия при различных температурах уравнение (1.116) проинтегрируем, но прежде запишем его в более удобной форме:

dlnK	P	=	∆H	dT .	(1.117)
			RT2

					45
В узком интервале температур (порядка несколько десятков градусов)
тепловой эффект химической реакции (∆H) не зависит от температуры.
Поэтому, после интегрирования (1.117) получим:
		lnKP	= − ∆H + B ,		(1.118)
			RT
где В — постоянная интегрирования.
					p
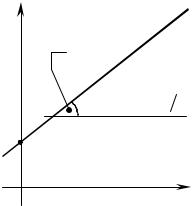
В соответствии с уравнением (1.118) lnKP есть					K
В соответствии с уравнением (1.118) lnKP есть					ln
линейная функция обратной температуры, т. е.					ln
линейная функция обратной температуры, т. е.					α
lnKP = f (1/T).	Тангенс	угла	наклона	прямой	tgα = −∆H R
lnKP = f (1/T) к оси абсцисс равен -∆Н/R, а отрезок					tgα = −∆H R
lnKP = f (1/T) к оси абсцисс равен -∆Н/R, а отрезок					B
на оси ординат соответствует постоянной интег-					B
рирования B = ∆S0/R (рис. 1.6).					B = ∆S/R
рирования B = ∆S0/R (рис. 1.6).
Таким образом, изучение химических равнове-					1/T
сий позволяет получить информацию не только для					Рис. 1.6. Графическое
расчета концентраций веществ, но и для определе-					представление
расчета концентраций веществ, но и для определе-					зависимости (1.118)
ния энтальпий и энтропий химических реакций.

1.11.3. Уравнение изохоры химической реакции

Для вывода уравнения изохоры химической реакции используем уравнение изотермы химической реакции (1 . 111) и уравнение Гиббса- Гельмгольца (1 . 72):

	∂∆F		(1.119)
∆F = ∆U + T	∂T	.
		V

Продифференцируем уравнение (1.111) по температуре при V = const:

	∂∆F		cc	cd		dlnK	C
		= R ln	Ca	Db − R lnKC − RT			C	.	(1.120)
		= R ln	Ca	Db − R lnKC − RT		dT		.	(1.120)
	∂T V		cA	cB		dT
В уравнение (1.119) вместо ∂∆F					подставим (1.120) и получим:
				∂T	V

− RT2

dlnK

∆F = ∆U + RT ln

D − RT lnK

(1.121)

caA cBb

Далее приравняем (1.111) и (1.121)

− RT2

dlnK

RT ln

D − RT lnK

= ∆U + RT ln

D − RT lnK

caA cBb

После преобразования этого уравнения получим:

∆U = RT2 dlnKdT C ,

или

dlnKC	=	∆U	.	(1.122)

dT		RT2

Уравнение (1.122) есть уравнение изохоры химической реакции.

Из уравнений изобары и изохоры следует, что константа химического равновесия увеличивается с ростом температуры в эндотермических ре- акциях (∆Н > 0). В случае экзотермической реакции (∆Н < 0) константа увеличивается с понижением температуры.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 3311 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>