Soprotivlenie_materialov / Все лекции Емельянова / Лекция-11+

7

ЛЕКЦИЯ №11

Прямой чистый изгиб. Нормальные напряжения при изгибе.

При прямом чистом изгибе в поперечных сечеиях бруса действуют только изгибающие моменты, а поперечные силы равны нулю. Изгибающие моменты вызывают нормальные напряжения в поперечных сечениях бруса.

Рассмотрим прямой брус. Предположим, что поперечное сечение бруса имеет хотябы одну ось симметрии, через которую проходит силовая плоскость изгиба, следовательно, ось симметрии сечения является главной центральной осью. Вторая главная центральная ось перпендикулярная первой и проходит через центр тяжести сечения.

Нагрузим брус в плоскости XOY ( в плоскости симметрии) парой сил, приложенных к торцевым сечениям. В результате имеем прямой чистый изгиб. Построим эпюры Q и M .

При выводе формул для нормальных напряжений вводятся допущения:

1. Плоские поперечные сечения бруса до деформации изгиба остаются плоскими и после деформации (гипотеза плоских сечений Бернули).

2. Продольные волокна бруса не давят друг на друга и следовательно в продольных сечениях нормальные напряжения равны нулю.

3. Нормальные напряжения по ширине сечения на данном уровне одинаковы, а по высоте сечения изменяются.

Данные допущения (гипотезы) подтверждаются опытами и точными расчётами теории упругости.

Рассмотирм опыт с изгибом резинового бруса. Нанесем на него сетку.

Приложим пары сил.

Продольные полосы сетки искривляются, а поперечные полосы остаются прямыми и лишь поворачиваются на некоторые углы. Это подтвержадет справедливость гипотезы плоских сечений. С выпуклой стороны волокна расстягиваются, а с вогнутой сжимаются. Имеется нейтральный продольный слой, который не ратсягивается и не сжимается. Линия по которой нетральный слой пересекает поперечные сечения называется нейтральной осью ( нейтральной линией).

Для получения формулы нормальных напряжений пр изгибе рассмотрим три стороны задачи: геометрическую,физическую и статическую.

1. Геометрические соотношения

Выделим из бруса двумя поперечными сечениями элементы длинной dx и рассмотрим его в изогнутом состоянии. На рисунке О-- нейтральный слой, - радиус кривизны нейтрального слоя. У нейтрального слоя длинна не меняется.

Определим относительное удлинение слоя b отстоящего от нейтрального слоя на расстоянии у

= =

(*)

2. Физические соотношения

Продольные волокна бруса испытывают простое растяжение ( сжатие) пр изгибе

Закон Гука при простом растяжении – сжатии

или . (**)

3. Статические соотношения.

Из шести интегральных зависимостей между усилиями и напряжениями бруса три обращаются в тождества

Ξ0,Ξ 0,Ξ0 так как =0 , =0.

Три других интегральных зависимости между усилиями и направлениями бруса запишем в следующем виде.

1. N

2. = (у нас нет

3. =

Исследуем первую интегральную зависимость

N==0

= - статический момент площади сечения относительно оси Z.

Так как ≠0, следовательно, = ось Z (нейтральная ось) проходит через цент тяжести сечения.

Исследуем вторую интегральную зависимость.

=0

=- центральный момент инерции относительно осей y,z.

Так как == 0. Следовательно, центробежный момент инерции относительно осей y,z=0 , то есть оси y,z являются главными центральными осями сечения.

Исследуем третью интегральную зависимость.

= = -осевой момент инерции сечения относительно оси z.

Следовательно, имеем следующее соотношение

(1)

где – кривизна изогнутой оси бруса в данной точке.

- жесткость поперечного сечения относительно оси z при изгибе.

Из зависимости (**) подставляя туда выражение (1) получим:

(2). Это формула нормальных напряжений при изгибе.

Формула (2) показывает, что изменяется по высоте балки по линейному закону, так как меняется только y. Покажем эпюру

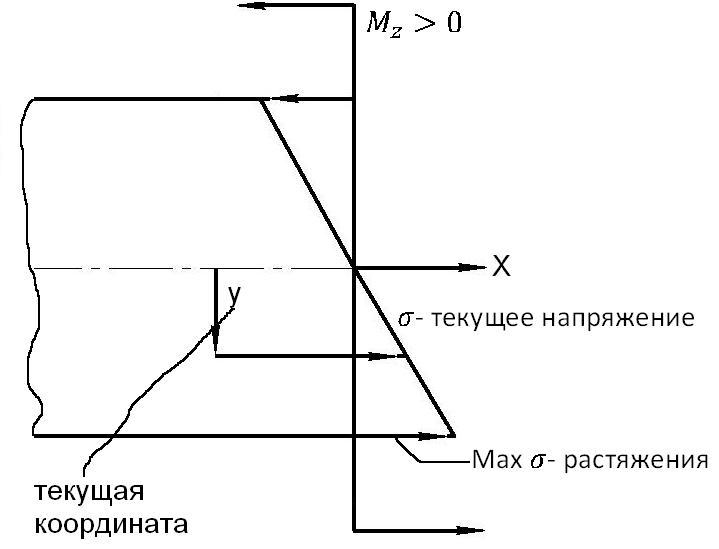
Растягивающие напряжения считаются положительными, а сжимающие отрицательными

max ==

max ==

Наибольшее напряжение, по модулю, будут в точке наиболее удалённой от нейтральной оси.

|max |= =

= –осевой момент сопротивления сечения относительно оси Z.

Условие прочности по нормальным напряжениям при изгибе

Наибольшие нормальные напряжения в балке не должны превышать допускаемых напряжений для материала.

Для балок из пластичных материалов, у которых []=[] условие прочности записывается

|max|= = ≤[].

Для балок не одинаково сопротивляющихся растяжению сжатию ([]≠[]) записываются два условия прочности. Одно условие прочности записывается для точки наиболее удалённой от нейтральной оси в сжатой зоне опасного сечения, другое условие записывается для точки наиболее удалённой от нейтральной оси в растянутой зоне того же сечения.

|max|= = ≤[],

|max|= = ≤[].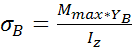