
Математика ЗО от Белоусовой / Математический анализ, практика 2 семестр / Практика 1
.doc-
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ПЕРВООБРАЗНАЯ, ЕЕ СВОЙСТВА. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, СВОЙСТВА.
Функция F(x)
называется первообразной для
функции
![]() ,
если
,
если
![]() .
.
Множество всех
первообразных
![]() функции
функции
![]() называется неопределенным интегралом
этой функции и обозначается
называется неопределенным интегралом
этой функции и обозначается
![]() :
:
![]()
Для вычисления неопределенных интегралов прежде всего следует знать свойства неопределенных интегралов и таблицу интегралов.
Таблица основных интегралов
1.
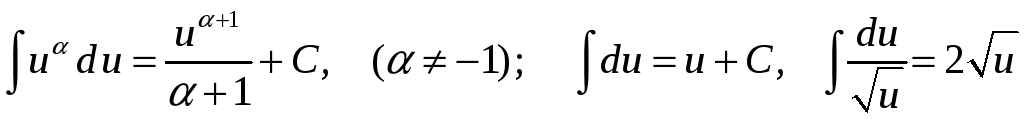 .
.
2.
![]() .
.
3.
 .
.
4.
![]() ,
,
![]()
5.
![]() ,
,
![]()
6.
![]() .
.
7.
![]() .
.
8.
 .
.
9.
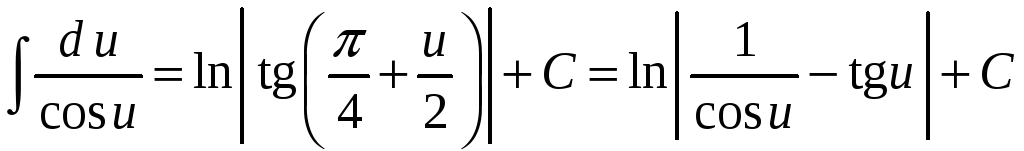 .
.
10.
![]() .
.
11.
 .
.
12.
 .
.
13.
 .
.
Рассмотрим отыскание неопределенного интеграла с помощью свойств интегралов, таблицы интегралов и алгебраических преобразований.
Пример 1. Найти интегралы
1)![]() ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.
Решение.
1)

 ;
;
2)
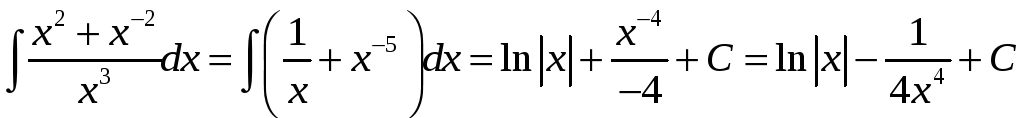 ;
;
3)
 ;
;
4)


Примеры для самостоятельного решения
Найти интегралы:
1.
 ,
2.
,
2.
 ,
3.
,
3.
![]() ,
4.
,
4.
![]() .
.
Ответы.
1.![]() ,
2.
,
2.![]() ,
3.
,
3. ,
4.
,
4.
 .
.
Метод подведения под знак дифференциала
|
Способ основан
на применении свойств дифференциалов:
|
Пример 2. Найти интегралы
1)
 ;
2)
;
2)
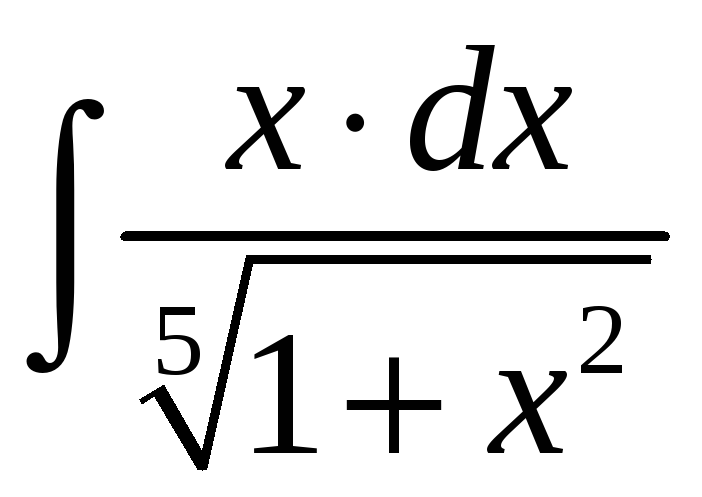 ;
3)
;
3)
![]() ;
4)
;
4)
 ;
5)
;
5)
![]() ;
;
6)
 ;
7)
;
7)
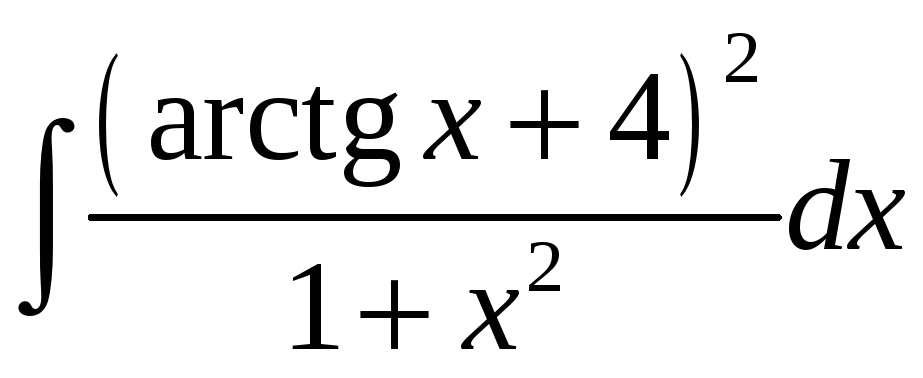 ;
8)
;
8)
 ;
9)
;
9)
 .
.
Решение
1)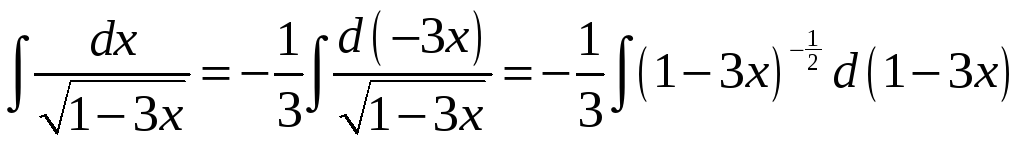
 ;
;
2)

![]() ;;
;;
3)
 ;
;
4)

![]() ;
;
5)
 ;
;
6)

![]() ;
;
7)
 ;
;
8)

![]() ;
;

Пример 3. Найти
интегралы : 1)
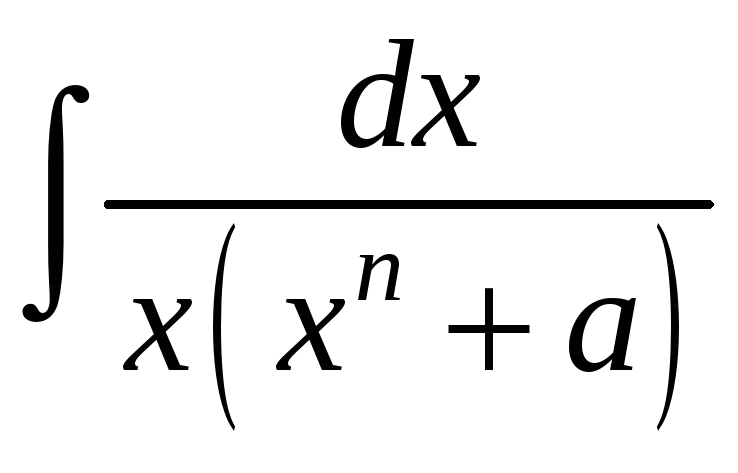 ;
2)
;
2)
 .
.
Решение. В этих интегралах присутствует «свободный» множитель x в знаменателе, поэтому выгодно будет вынести из скобки или из-под корня старшую степень x и подвести ее под знак дифференциала:
1)

 ,
,

 .
.
Примеры для самостоятельного решения
1.
![]() ,
2.
,
2.
![]() ,
3.
,
3.
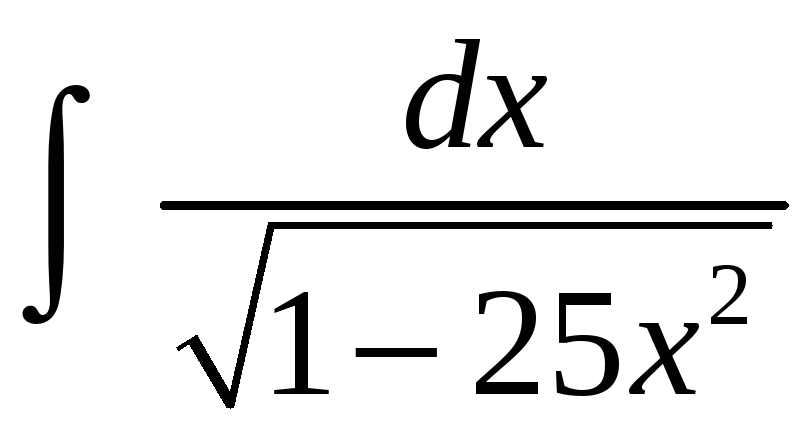 ,
4.
,
4.
 ,
5.
,
5.
![]() ,
,
6.
 ,
7.
,
7.
 8.
8.
 ,
9.
,
9.
![]() ,
10.
,
10.
![]() ,
,
11.
 ,
12.
,
12.
 .
.
Ответы.
1.
![]() ,
2.
,
2.
![]() ,
3.
,
3.
![]() ,
4.
,
4.
![]() ,
5.
,
5.
![]() ,
,
6.
![]() ,
7.
,
7.
![]() ,
8.
,
8.
![]() ,
9.
,
9.
![]() ,
,
10.
![]() ,
11.
,
11.
![]() ,
12.
,
12.
![]() .
.
Оглавление
1.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ПЕРВООБРАЗНАЯ, ЕЕ СВОЙСТВА. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ, СВОЙСТВА. 1
Таблица основных интегралов 1
Ответы. 3
Метод подведения под знак дифференциала 3
Ответы. 6
Оглавление 7
