2. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ.

Если функции и дифференцируемы, тогда справедлива формула

.

Данная формула применяется в случаях, когда подынтегральное выражение можно представить в виде произведения двух множителей и , причем по виду функции легко можно восстановить функцию , и вычисление интеграла является более простой задачей, чем вычисление интеграла .

Укажем, как выбирать множители и в некоторых случаях:

1. в интегралах вида , где  многочлен, в качестве “u” выбираем многочлен: , чтобы понизить его степень;

2. в интегралах вида за “u” следует взять функции . В противном случае трудно восстановить функцию по её дифференциалу.

Пример. Найти неопределенные интегралы :

1) , 2), 3), 4), 5).

Решение

1). . Используя рекомендации, положим , . Тогда , . Используя формулу (7.2), получим:

.

2). .

3).

4) . Положим ; тогда

, .

Таким образом,

.

5) =

Таким образом, имеем: или .

Тогда . Мы получили одну из первообразных. Чтобы записать множество первообразных, нужно добавить произвольное число C:

.

Пример. Найти интеграл .

Положим . Здесь такой выбор и менее очевиден, чем в предыдущих примерах. В выражение для мы включили , чтобы получить d(sin x) и легко вычислить v: .

Тогда по формуле интегрирования по частям получим

.

Здесь использована формула 8, п.7.1.

Примеры для самостоятельного решения

Найти интегралы: 1. , 2. , 3. ,

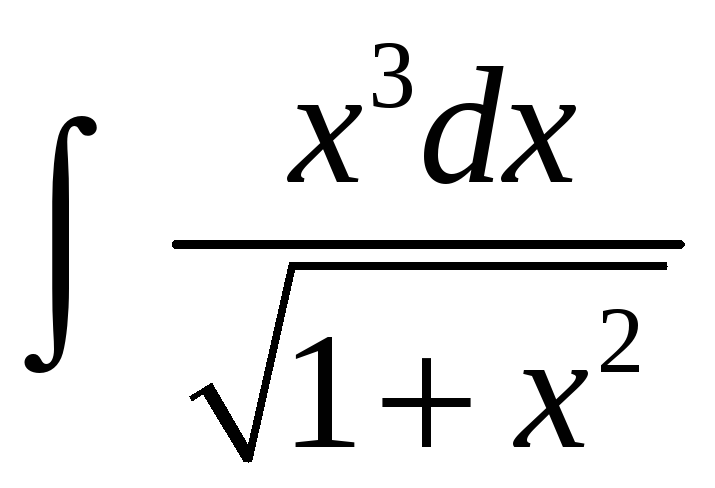4. , 5. , 6. .

Указания. В 4-м примере положить и учесть, что

.

В 5-м примере положить .

В 6-м примере применить метод интегрирования по частям 2 раза.

Ответы.

1., 2. , 3. , 4., 5. , 6..

Оглавление

2. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ. 1

Пример. Найти неопределенные интегралы : 1

Ответы. 4

Оглавление 5