17. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ЛИНЕЙНЫЙ ИНТЕГРАЛ И ЕГО ВЫЧИСЛЕНИЕ.

Определение. Линейным интегралом поля по дуге называется интеграл .

Правила вычисления линейных интегралов:

1. Для вычисления интеграла по линии , заданной уравнениями , следует

а) заменить в функциях соответственно на ;

б) заменить соответственно на ;

в) найти интервал изменения параметра и вычислить получившийся

определенный интеграл по этому интервалу.

2. Для вычисления интеграла по плоской линии с уравнением следует

а) заменить в функциях на ;

б) заменить на ;

в) вычислить получившийся определенный интеграл по отрезку .

Пример 1. Вычислить линейный интеграл в поле вектора вдоль части астроиды , лежащей в первой четверти (рис. 1).

Решение. Из системы уравнений найдем значение параметра , соответствующее точке A, а из системы уравнений – значение , соответствующее точке B.

Вычислим линейный интеграл .

Так как , то , следовательно, .

Пример 2. Вычислить работу силового поля вдоль первой арки циклоиды .

Решение. Работа А силы вычисляется по формуле

.

В нашем случае .

Кривая задана параметрическими уравнениями:

, .

Найдем ; .

Тогда работа

.

Пример 3. Вычислить линейный интеграл в векторном поле вдоль параболы в направлении возрастания параметра.

Решение. Линия задана уравнением , поэтому на линии имеем: , ;

.

Тогда .

(Воспользовались тем, что интеграл от нечетной функции по отрезку равен нулю, а от четной функции .)

Пример 4. Вычислить работу силы при перемещении единичной массы по контуру, образованному линией пересечения сферы с координатными плоскостями , в положительном направлении обхода контура.

Решение. .

Контур состоит из дуг окружностей единичного радиуса с центром в начале

координат, расположенных в координатных плоскостях (рис. 2).

По свойству аддитивности

.

Рассмотрим каждый из интегралов.

Так как дуга AB имеет уравнение: , то .

Тогда и

.

Аналогично, для дуги ВС: ,

;

.

Для дуги СA: ,

,

.

Таким образом,

.

Циркуляция. Формула Грина

В тех случаях, когда линейный интеграл поля берется по замкнутой кривой , он называется циркуляцией поля (вектора) по кривой и обозначается так:

Для вычисления циркуляции поля по плоской кривой удобно использовать формулу Грина:

Пример 5. Найти циркуляцию вектора по кривой, составленной из правой половины эллипса и отрезка

оси (рис. 3).

Решение. Воспользуемся формулой: .

На эллипсе , , .

При движении по дуге эллипса в направлении против часовой стрелки параметр меняется от до .

Таким образом,

.

На отрезке : , , ;

и .

Значит искомая циркуляция равна нулю.

Пример 6. Вычислить циркуляцию вектора по контуру :

Решение. По формуле имеем:

.

Контур есть окружность , лежащая в плоскости . Запишем параметрические уравнения этой окружности: .

На контуре : , .

Выберем положительный обход контура (против часовой стрелки).

Тогда

.

Пример 7. Вычислить циркуляцию вектора по контуру : .

Решение. Очевидно, что непосредственно вычислить циркуляцию, используя параметрические уравнения кривой, в данной задаче довольно затруднительно, поэтому, учитывая, что контур замкнутый, воспользуемся формулой Грина.

Так как , то циркуляция

.

В нашем примере , , 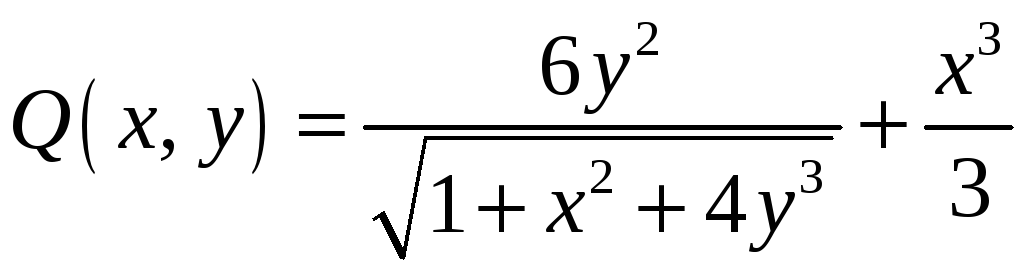тогда , , то есть .

Контур : – окружность радиуса 1, область – круг, ограниченный этой окружностью.

Таким образом, применив формулу, имеем:

.

(В двойном интеграле перешли к полярной системе координат , .)

Ротор. Теорема Стокса

Определение. Ротором векторного поля называется вектор

.

Понятие ротора позволяет удобно вычислять циркуляцию векторного поля по пространственной кривой , опираясь на следующую формулу Стокса:

.

В этой формуле ─ любая поверхность, натянутая на контур , причем ориентации контура и поверхности согласованы, т. е., глядя с конца выбранных нормальных векторов поверхности , обход контура виден

против часовой стрелки.

Пример 8. Вычислить циркуляцию вектора вдоль контура : используя теорему Стокса.

Решение. По формуле Стокса циркуляция

,

где – любая поверхность, натянутая на контур .

Контур – эллипс, получаемый при пересечении цилиндрической поверхности с плоскостью (рис. 4); поверхность – часть плоскости , ограниченная эллипсом .

Ориентация контура и поверхности показана на рис. 4.

Найдем нормаль к поверхности : , .

Вычислим , тогда , значит, по теореме Стокса .

Пример 9. Вычислить циркуляцию вектора вдоль контура : непосредственно и по теореме Стокса.

Решение. Контур – линия пересечения сферы и конуса .

Найдем уравнение этой линии: . Учитывая, что , получаем уравнение окружности , лежащей в плоскости .

Запишем параметрические уравнения этой окружности: .

Тогда , , откуда

.

Вычислим теперь циркуляцию по теореме Стокса.

Найдем : .

В качестве поверхности возьмем круг, лежащий в плоскости , с границей . Тогда и .

Итак,

.

Некоторые классы векторных полей.

Потенциальное поле

Определение. Векторное поле называется потенциальным, если оно является полем градиента некоторой скалярной функции , т.е. ; при этом функцию называют скалярным потенциалом векторного поля.

Свойства потенциального поля

1). Поле является потенциальным с потенциалом тогда и только тогда, когда .

2). В потенциальном поле линейный интеграл не зависит от формы пути.

3). В потенциальном поле циркуляция по любому замкнутому контуру равна нулю.

4). Поле потенциально тогда и только тогда, когда в каждой точке поля .

5). В потенциальном поле линейный интеграл по дуге равен разности потенциалов конца и начала дуги.

Пример 10. Показать, что поле вектора потенциально, найти работу в поле вектора при перемещении по линии : от точки до точки .

Решение. Покажем что поле потенциально. Запишем . Тогда по свойству 1 поле потенциально и – его потенциал. В потенциальном поле линейный интеграл (а значит, и работа) по дуге кривой равен разности потенциалов конца и начала дуги.

Таким образом, работа .

Пример 11. Найти потенциал поля , если: 1) , 2) .

Решение. Известно, что центральное поле вектора потенциально и его потенциал равен , поэтому:

1) ;

2) .

Пример 12. Является ли поле вектора потенциальным? Если да, найти его потенциал.

Решение. Проверим потенциальность поля по условию .

Найдем по формуле (11.1):

,

значит, поле потенциально и , или в координатной форме , .

Проинтегрируем первое из этих равенств по :

.

Подставим полученную функцию во второе равенство и найдем :

,

то есть .

Найдем : .

Таким образом, имеем .

Соленоидальное поле. Гармоническое поле

Определение. Поле называют соленоидальным, если оно является полем ротора некоторой векторной функции , т.е. ; при этом вектор называют векторным потенциалом поля .

Свойства соленоидального поля

1). Поле является соленоидальным тогда и только тогда, когда .

2). В соленоидальном поле поток через замкнутую поверхность, не содержащую внутри особых точек поля, равен нулю.

3). В соленоидальном поле потоки через замкнутые поверхности, окружающие особую точку поля, равны между собой.

Определение. Поле , являющееся одновременно и потенциальным, и соленоидальным, называется гармоническим полем.

Пример 13. Какие из следующих векторных полей являются соленоидальными

1) ,

2) ?

Решение. Поле вектора соленоидально, если .

Так как , то поле вектора не является соленоидальным;

, значит, поле вектора соленоидально.

Пример 14. Проверить, что поле вектора является гармоническим.

Решение. Поле вектора называется гармоническим, если оно одновременно является и потенциальным, и соленоидальным, то есть и .

Вычислим и :

, ; поле является гармоническим.

Пример 15. Являются ли гармоническими следующие функции:

1) , 2) ?

Решение. Функция называется гармонической, если она удовлетворяет уравнению Лапласа или , где .

1). Найдем : , тогда ; .