7. Практическое занятие Определенный интеграл.

Пусть на отрезке задана функция . Разобьем отрезок произвольным образом на ячеек с длинами . В этих ячейках выберем произвольно точки . Составим интегральную сумму . Найдем предел интегральной суммы при стремлении к нулю ─ максимальной из длин ячеек.

Если существует предел интегральной суммы при , не зависящий от способа разбиения отрезка и от выбора промежуточных точек , то этот предел называется определенным интегралом функции по отрезку и обозначается Итак,

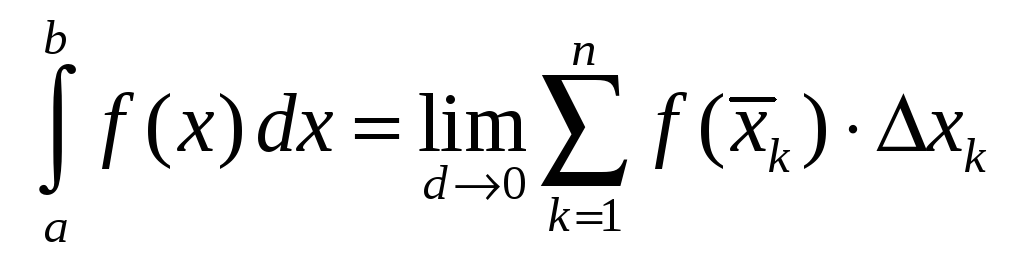
Свойства определенного интеграла

1) .

2) ─ для любого расположения точек .

3). Если на , то

4). Если на отрезке , то .

5). .

6). Если функция непрерывна на отрезке , то на этом отрезке найдется точка такая, что

Значение называют средним значением функции на отрезке :

7). Пусть функция непрерывна на отрезке . Тогда производная определенного интеграла от этой функции по переменному верхнему пределу равна

значению подынтегральной функции на верхнем пределе, т.е.

Пример 1. Оценить интеграл .

Решение. По свойству 4) имеем: , где ─ наименьшее, ─ наибольшее значения функции на отрезке .

Найдем и для функции на отрезке . Вычислим:

1) производную ;

2) критические точки, решив уравнение знаменатель на отрезке в нуль не обращается; поэтому других критических точек нет;

3) значения функции в критических точках и на концах отрезка:

; ; , .

Из множества полученных значений наименьшее значение и наибольшее значение . Поэтому

или .

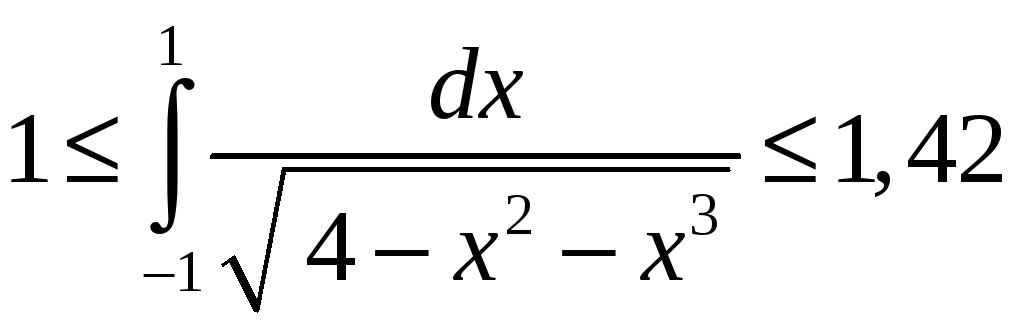Пример 2. Доказать, что .

Решение. Нужно оценить интеграл . Известно, что функция монотонно убывает на промежутке , следовательно, и на отрезке . Тогда наименьшее значение функции равно значению , а наибольшее , т.е. , , и по свойству 4) имеем: , что и требовалось доказать.

Пример 3. Пользуясь неравенствами доказать, что

.

Решение. Функция не определена в точке . Вычислим предел этой функции, воспользовавшись тем, что при :

Доопределим функцию , положив , тогда функция будет непрерывна на отрезке . По условию, выполняются неравенства

, а значит и неравенства

По теореме об интегрировании неравенств получим

.

Вычислим интегралы: ;

.

Получим: , что и требовалось доказать.

Пример 4. Определить какой интеграл больше: или .

Решение. Рассмотрим подынтегральную функцию . Так. как функция убывающая на промежутке , то

на и на .

Умножив неравенства на , получим

на , на .

По теореме об интегрировании неравенств имеем:

и .

Вычислим интегралы

, .

Тогда , .

Сравнив результаты, получим:

.

Пример 5. Найти среднее значение функции на отрезке .

Решение. По свойству 6) имеем . Вычислим интеграл и среднее значение функции:

Пример 6. Вычислить , если 1) ; 2) функция задана параметрическими уравнениями .

Решение. 1). По свойству 7) имеем: .

Используем следующие свойства определенного интеграла:

, .

Тогда

.

Функции и есть сложные функции переменной . Действительно, , где ; , где .

Используя формулу вычисления производной сложной функции, получим:

, .

Следовательно, .

2). Для функции , заданной параметрическими уравнениями , , имеем: . Вычислим и .

,

Примеры для самостоятельного решения

Оценить интегралы , , .

Выяснить, какой из интегралов больше:

а) или ; б) или .

Найти производную для функции , заданной параметрическими уравнениями .

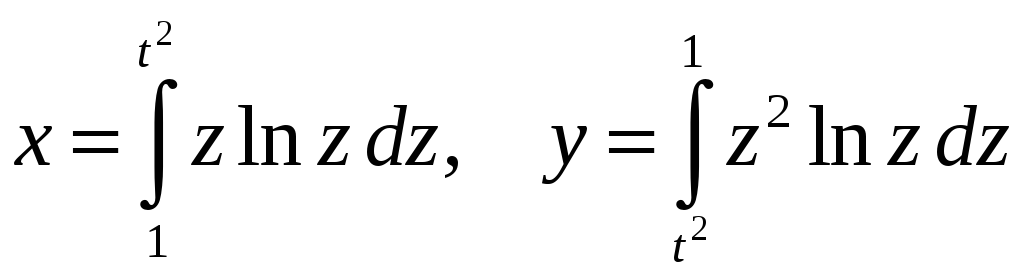Найти точки экстремума функции .

Найти среднее значение функции

а) на отрезке ; б) на отрезке .

Ответы:

1) , , ; 2а) второй; 2б) второй; 3) ;

4) точки максимума , точка минимума ; 5а) ; 5б) .

Оглавление

7. Практическое занятие Определенный интеграл. 1

Свойства определенного интеграла 1

Примеры для самостоятельного решения 5

Ответы: 6

Оглавление 7