6. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.

Перед интегрированием рациональной дроби надо сделать следующие алгебраические преобразования и вычисления:

1) если дана неправильная рациональная дробь, то выделить из нее целую

часть, то есть представить в виде , где M(x) – многочлен, а – правильная рациональная дробь;

2) разложить знаменатель дроби на линейные и квадратные множители: , где , то есть трехчлен имеет комплексно сопряженные корни и значит, не разлагается на линейные множители;

3) правильную рациональную дробь разложить на простейшие дроби:

4) вычислить коэффициенты .

В результате интегрирование рациональной дроби сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.

Пример 1. Найти интеграл

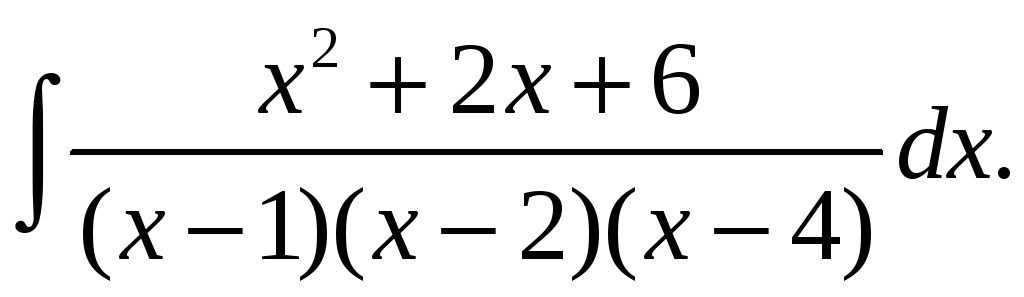
Решение. Данную рациональную дробь можно представить в виде суммы простейших дробей следующего вида:

Умножив это равенство на , получим:

.

Положим в этом равенстве , тогда , откуда . Полагая , получим , ; полагая , имеем , .

Итак, разложение рациональной дроби на простейшие имеет вид

Таким образом,

Пример 2. Найти интеграл

Решение. Разложим подынтегральную функцию на простейшие дроби. Множителю соответствует сумма трех дробей, а множителю − только одна дробь:

Умножив это равенство на , получим:

.

Полагая в этом равенстве и , получим:

.

Для отыскания сравним коэффициенты в равенстве при старшей степени х, то есть при . В левой части нет члена с , то есть коэффициент при равен 0. В правой части коэффициент при равен C+D. Поэтому, значит, .

Сравним коэффициенты при или придадим какое-нибудь значение. Пусть , тогда , или , т.е. .

Итак, ,

Пример 3. Найти интеграл .

Решение. Разложим знаменатель на множители Тогда

.

Умножив это равенство на , получим:

При имеем ; при имеем .

Для отыскания еще трех коэффициентов сравним в равенстве коэффициенты при степенях х:

Получим , и .

Следовательно,

.

Пример 4. Найти интеграл .

Решение. Выделим целую часть неправильной дроби, поделив числитель на знаменатель: . Тогда

.

Пример 5. Найти интеграл

Решение. Подынтегральная функция является правильной рациональной дробью, можно найти интеграл, представив дробь в виде суммы простейших дробей. Однако нахождение интеграла можно значительно упростить, если произвести замену переменной , тогда . В результате получим:

Примеры для самостоятельного решения

Найти интегралы: 1. , 2. , 3. ,

4. , 5. , 6. .

Указания: в примере 1 учесть, что ;

в примере 4 учесть, что .

Ответы.

1., 2. ,

3., 4. ,

5., 6. .

Оглавление

6. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ. 1

Примеры для самостоятельного решения 4

Ответы. 4

Оглавление 5