13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ТРОЙНОЙ ИНТЕГРАЛ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ.

Пусть тело ограничено поверхностями , , цилиндрической поверхностью с образующими, параллельными оси . Тогда

,

где – есть проекция тела на плоскость .

Чтобы применять формулу на практике, рекомендуем:

1) построить тело ;

2) записать тройной интеграл через повторный интеграл; в повторном интеграле сначала расставить внутренние пределы интегрирования, т.е. пределы изменения . Для этого надо двигаться параллельно оси . При этом мы войдем в тело через поверхность, на которой , а выйдем через поверхность, на которой . Таким образом, переменная интегрирования меняется от до ;

3) вычислить внутренний интеграл при фиксированных ;

4) вычислить внешний интеграл по проекции тела на плоскость .

Пусть тело ограничено поверхностями , и цилиндрической поверхностью с образующими, параллельными оси . Тогда

Пусть тело ограничено поверхностями , и цилиндрической поверхностью с образующими, параллельными оси . Тогда

Пример 1. Вычислить , если тело ограничено поверхностями .

Решение. Снизу тело ограничено плоскостью , сверху – плоскостью , сбоку – цилиндрической поверхностью (рис. 1), поэтому можно воспользоваться формулой.

В двойном интеграле расставим пределы интегрирования, учитывая рекомендации. Тогда

.

Пример 2. Вычислить момент инерции относительно плоскости однородного тела , ограниченного поверхностями

.

Решение. Найдем момент инерции по формуле

.

Так как тело однородное, то .

Построим тело, ограниченное плоскостями

(рис. 2)

Снизу тело ограничено плоскостью , сверху – плоскостью , сбоку цилиндрическими поверхностями с образующими, параллельными оси , поэтому можно воспользоваться формулой. При расстановке пределов интегрирования в двойном интеграле учтем, что проекция тела на плоскость – треугольник, ограниченный прямыми . Тогда

.

Пример 3. Найти объем тела, ограниченного поверхностями

.

Решение. Справа тело ограничено поверхностью (параболоид), слева – поверхностью , сверху и снизу – цилиндрическими поверхностями с образующими, параллельными оси . Здесь удобнее спроецировать тело на плоскость , поэтому воспользуемся формулой. Тогда .

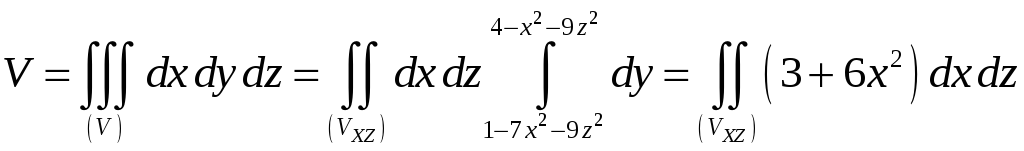Построим проекцию тела на плоскость (рис. 3). Найдем точки пересечения парабол:

.

Расставим пределы интегрирования, учитывая рекомендации:

.

Пример 4. Найти объем тела, ограниченного поверхностями

.

Решение. Сверху тело ограничено плоскостью , снизу – плоскостью , сбоку – цилиндрической

поверхностью с образующими, параллельными

оси (рис.4). Поэтому .

Найдем линию пересечения плоскостей:

.

Проекция ограничена параболой и прямой (рис. 5). Найдем точки пересечения этих линий:

.

Таким образом, имеем:

.

Тройной интеграл в цилиндрической системе координат

В цилиндрической системе координат положение точки в пространстве однозначно определяется тройкой чисел , где – полярные координаты проекции точки на плоскость , – аппликата точки .

Переход к цилиндрической системе координат осуществляется по формулам

.

В некоторых случаях удобно переходить к обобщенной цилиндрической системе координат:

.

Пример 5. Найти объем тела, ограниченного поверхностями

.

Решение. Уравнение задает сферу, а уравнение – параболоид. Найдем линию пересечения поверхностей:

(посторонний корень),

Проекция тела на плоскость ограничена окружностью (рис. 6).

Перейдем к цилиндрическим координатам, пользуясь формулами (3.4):

.

Запишем уравнения поверхностей в этих координатах:

(параболоид);

, но нас интересует только верхняя часть сферы, поэтому .

Уравнение окружности в полярных координатах имеет вид: , причем .

Учитывая вышесказанное, имеем:

.

Пример 6. Найти центр тяжести однородного круглого конуса высотой и радиусом .

Решение. Уравнение произвольного конуса имеет вид:

.

Чтобы найти коэффициент k, подставим начальные условия в уравнение конуса. Тогда . Таким образом, уравнение конуса примет вид: .

Найдем координаты центра тяжести .

Так как конус однородный () и симметричный относительно оси (рис. 7), то , а .

Воспользуемся геометрическим смыслом тройного интеграла

.

Для вычисления перейдем к цилиндрическим координатам по формулам: .

Запишем уравнение конуса в этих координатах:

, (на верхней части конуса ).

Таким образом,

.

Тогда . Итак, центр тяжести .

Пример 7. Найти объем тела, ограниченного поверхностями

.

Решение. Пользуясь формулами, преобразуем уравнения поверхностей:

, , .

Проекция тела на плоскость изображена на рис. 8.

Найдем объем тела, учитывая вышеизложенное:

.

Тройной интеграл в сферической системе координат

В сферической системе координат положение точки в пространстве однозначно определяется тройкой чисел , где – длина радиус-вектора точки ; – угол между радиус-вектором точки и положительным направлением оси ; – угол между осью и проекцией радиус-вектора точки на плоскость , причем .

Переход к сферической системе координат осуществляется по формулам:

.

Пример 8. Найти момент инерции однородного шара относительно касательной плоскости.

Решение. Введем систему координат таким образом, чтобы касательная плоскость совпала с координатной плоскостью , а центр шара находился на оси (рис. 9). Найдем момент инерции относительно плоскости по формуле . Запишем уравнение сферы:

или , где – радиус шара.

Перейдем к сферической системе координат, используя формулы:

.

Преобразуем уравнение сферы:

, , где , .

Учитывая, что , имеем

.

Пример 9. Найти объем тела, заданного неравенствами

.

Решение. Перейдем к сферической системе координат. Преобразуем неравенства, используя формулы:

. .

Рассмотрим проекции тела на плоскости (рис. 10) и (рис. 11).

В плоскости : , то есть . Найдем пределы изменения . Преобразуем равенство :

.

Учитывая неравенства (рис. 11), имеем: .

Таким образом, в сферической системе координат тело задается неравенствами: , , .

Итак,

.

Оглавление

13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ТРОЙНОЙ ИНТЕГРАЛ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ. 1

Тройной интеграл в цилиндрической системе координат 6

Тройной интеграл в сферической системе координат 9

Оглавление 13