16. Практическое занятие. Поток и его вычисление.

Определение. Потоком векторного поля через ориентированную поверхность называется величина

, где – скалярное произведение вектора поля на единичный вектор нормали к поверхности .

Пример 1. Вычислить поток вектора через площадку, имеющую форму треугольника с вершинами в точках , , , по направлению нормали, направленной в сторону начала координат.

Решение. Воспользуемся формулой.

Поверхность – треугольник , лежащий в плоскости (рис. 1). Единичный вектор нормали , поэтому . Учитывая, что площадь треугольника равна 1, получим

.

Пример 2. Вычислить поток векторного поля через внешнюю сторону части сферы , расположенной в первом октанте .

Решение. Нормальный вектор к сфере коллинеарен радиус-вектору (рис. 2), тогда вектор , так как на сфере .

Вычислим на поверхности сферы:

Тогда , где .

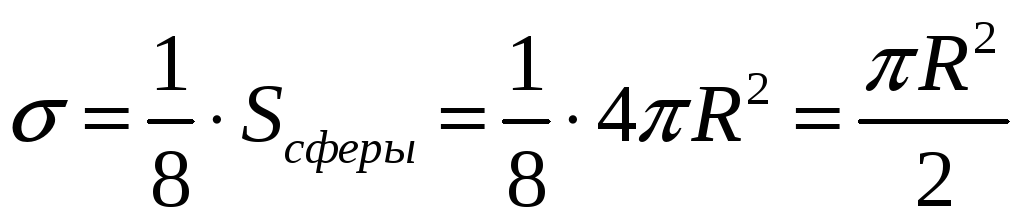Таким образом, .

Пример 3. Вычислить поток векторного поля через плоский треугольник, получаемый при пересечении плоскости с координатными плоскостями в положительном направлении оси .

Решение. Нормальный вектор плоскости равен , единичный вектор .

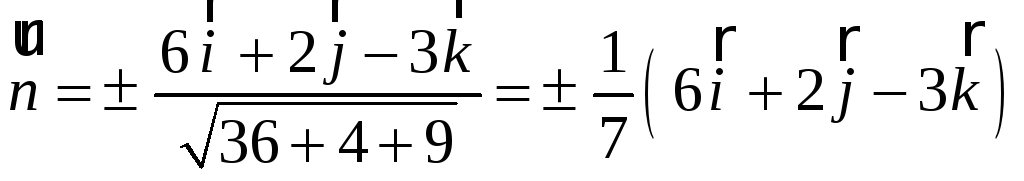Так как вектор по условию задачи составляет с осью острый угол, то , следовательно , .

Найдем скалярное произведение :

.

Тогда .

Для вычисления поверхностного интеграла воспользуемся формулой .

Выразим переменную из уравнения плоскости: , тогда

.

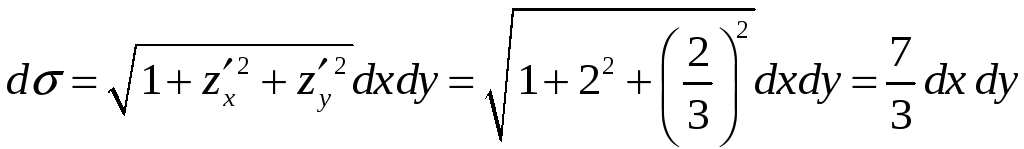Проекция треугольника ABC на плоскость есть треугольник AOC

(рис. 3).

Таким образом,

.

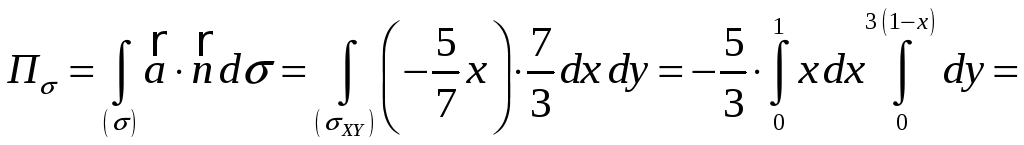
Пример 4. Вычислить поток вектора через внешнюю сторону цилиндрической поверхности , ограниченной сферой .

Р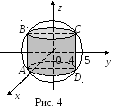ешение. Проекцией цилиндрической поверхности на плоскость является окружность 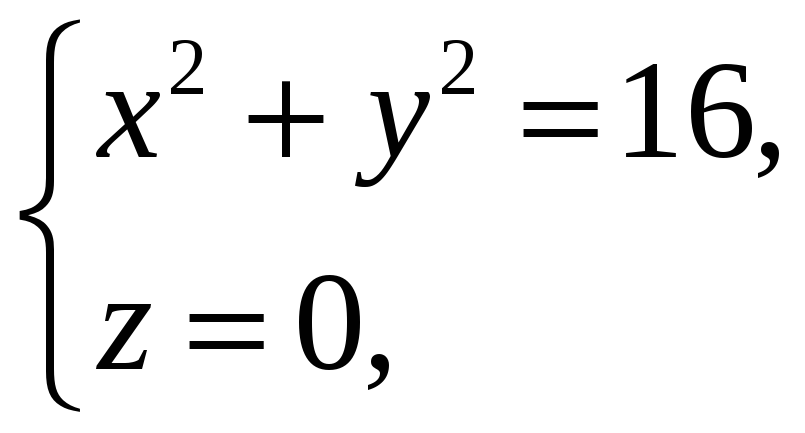поэтому рассмотрим проекцию цилиндрической поверхности, например, на плоскость – прямоугольник ABCD (рис. 4).

Так как цилиндрическая поверхность проецируется на плоскость невзаимнооднозначно, то, по свойству аддитивности, искомый поток , где – часть цилиндрической поверхности , – часть той же поверхности при .

Рассмотрим поверхность : . Найдем вектор нормали: , , .

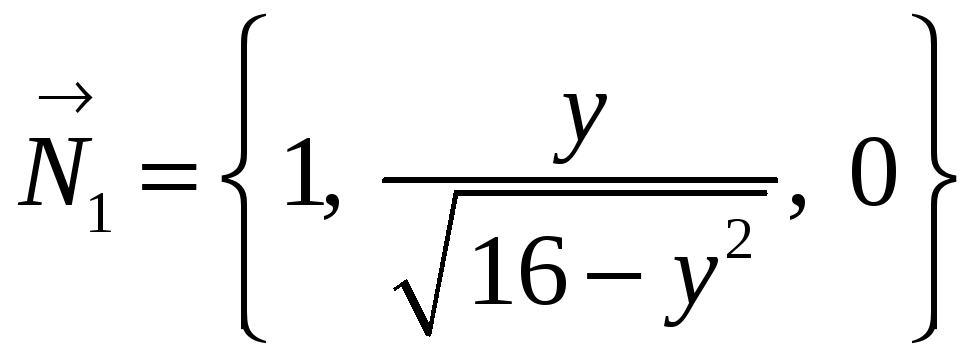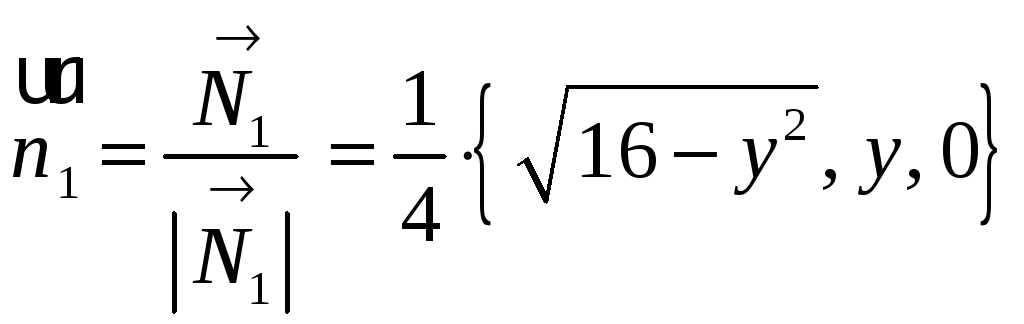Тогда , .

, где – прямоугольник ABCD.

Рассмотрим теперь поверхность : . Вектор нормали: , , , .

Тогда , .

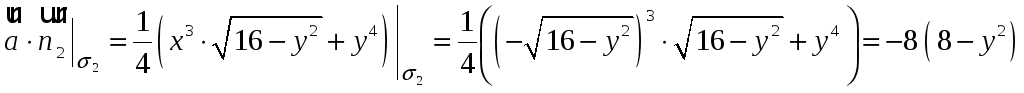Таким образом, .

Поток через замкнутую поверхность

Поток векторного поля через замкнутую поверхность удобно вычислять по формуле Остроградского

,

где ,

– тело, ограниченное замкнутой поверхностью , причём поверхность ориентирована внешней нормалью.

Пример 5. Найти поток поля вектора через замкнутую поверхность : , , .

Решение. Воспользуемся формулами.

Вычислим .

Тогда , где – объём усеченного конуса (рис. 5).

, то есть .

Пример 6. Найти поток поля вектора через замкнутую поверхность : , в направлении нормали, направленной внутрь тела.

Решение. В формуле Остроградского поверхность ориентирована внешней нормалью. Поток в направлении внутренней нормали будет равен значению потока, вычисленного по формуле Остроградского, с противоположным знаком.

Вычислим .

Тогда .

Для вычисления тройного интеграла воспользуемся рекомендациями п.3. Сверху тело ограничено плоскостью (рис. 6). Рассмотрим проекцию тела на плоскость (рис. 7). Справа и слева фигура ограничена линиями и , .

Тогда

.

Пример 7. Вычислить поток поля вектора через боковую поверхность тела, ограниченного поверхностями , , в направлении внешней нормали.

Решение. Воспользоваться формулой Остроградского непосредственно нельзя, так как наша поверхность незамкнутая, поэтому вычислим поток через боковую поверхность тела по формуле , где – поток через замкнутую поверхность, – поток через основание тела в направлении внешней нормали.

По формуле (8.1) вычислим :

.

Для вычисления интеграла перейдем к цилиндрической системе координат:

, , , .

Тогда уравнение параболоида примет вид . Проекцией тела на плоскость является круг

или (рис. 8).

.

Найдем поток через плоскость основания в направлении внешней

нормали (рис. 8):

, тогда и .

Таким образом, .

Пример 8. Вычислить поток поля вектора через боковую поверхность тела, расположенного в IV октанте и ограниченного поверхностями .

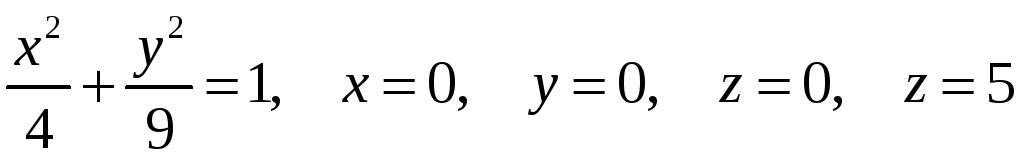Решение. Воспользуемся формулой .

Сначала вычислим поток через замкнутую поверхность тела по формуле: .

Так как проекцией тела на плоскость является часть плоскости, ограниченная эллипсом (рис. 9), то для вычисления тройного интеграла перейдем к обобщенной цилиндрической системе координат: , , .

Тогда , уравнение эллипса примет вид:

или , .

.

Вычислим поток через основания:.

Поверхность задана уравнением , единичный вектор нормали (рис. 9), поэтому и .

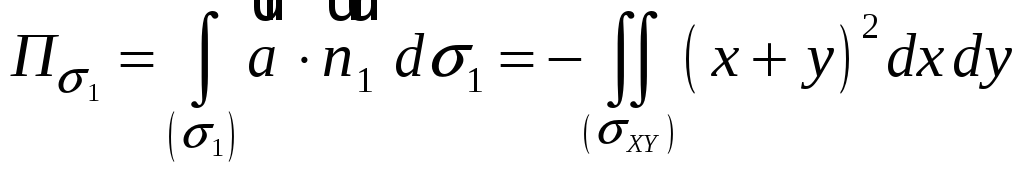Поверхность задана уравнением , единичный вектор нормали (рис. 9), поэтому и

.

Таким образом, и .

Оглавление

16.Практическое занятие. Поток и его вычисление. 1

Поток через замкнутую поверхность 5

Оглавление 10