3. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ.

Во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к более простому. Такой метод называется методом замены переменной или методом подстановки.

Пусть функция непрерывно дифференцируема на некотором промежутке и имеет обратную функцию . Тогда

Выражение, стоящее в правой части этой формулы, означает, что после отыскания интеграла вместо x нужно подставить его выражение через u.

При замене переменной в интеграле нужно

а) заменить переменную u на функцию  (x), заменить на ,

б) вычислить получившийся интеграл,

в) результат выразить через первоначальную переменную u.

Укажем некоторые рекомендации по выбору новой переменной. Пусть −рациональная функция , полученная из с помощью сложения, вычитания, умножения, деления. Рекомендации по выбору новой переменной приведены в следующей таблице.

Тип интеграла	Замена
	, k-наименьшее общее кратное чисел m,n

Пример. Найти неопределенные интегралы:

1) 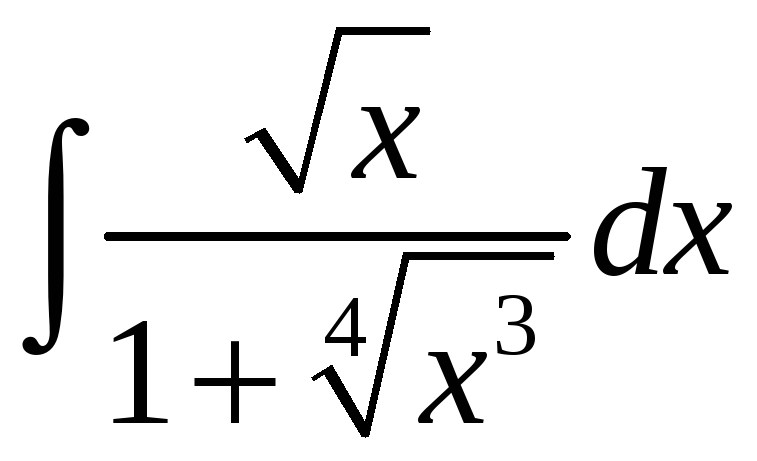; 2) ; 3) ; 4) .

Решение. 1). Для вычисления интеграла типа произведем замену переменной: , тогда и

.

Выделим целую часть дроби .

Таким образом,

.

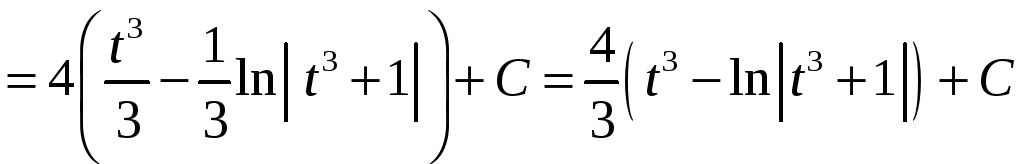Вернемся к переменной x, заменив . Тогда .

2). Для вычисления интеграла типа положим откуда . Тогда

.

3). Для вычисления интеграла положим . Тогда

.

Следовательно,

.

4). Для вычисления интеграла положим . Тогда , . Отсюда . Вычислим полученный интеграл с помощью формулы интегрирования по частям. Положим , тогда и

.

Вернемся к переменной x, заменив . Тогда .

Пример. Найти интеграл .

Решение. Имеем интеграл типа . Положим , тогда ,

Вернемся к прежней переменной х:

.

Следовательно, .

Пример. Найти интеграл .

Решение. Имеем интеграл типа . В соответствии с рекомендацией положим . Тогда ,

.

Вернемся к прежней переменной х:

, следовательно, , 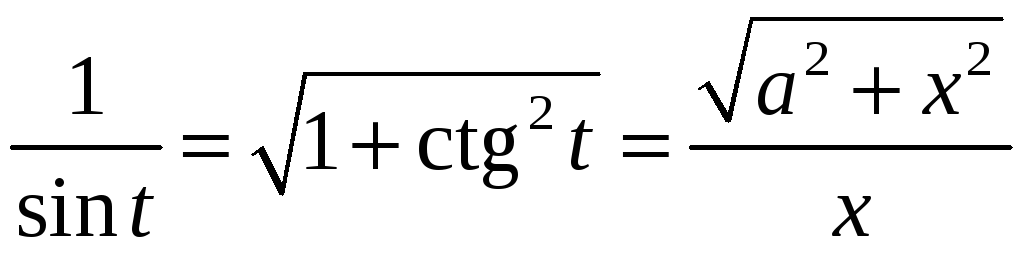. Итак,

.

Пример. Найти интеграл .

Решение. Имеем интеграл типа . Сделаем замену , .

Тогда

.

Первый интеграл находится методом интегрирования по частям (пример 7.5):

.

Второй интеграл − по формуле (8), п. 7.1.: 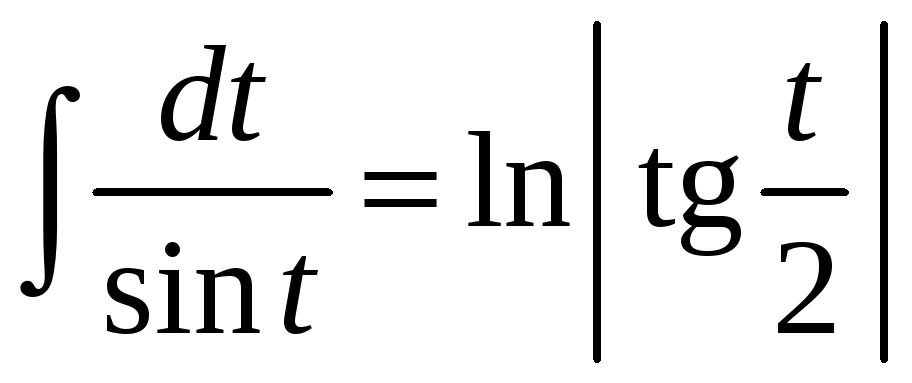. Итак,

.

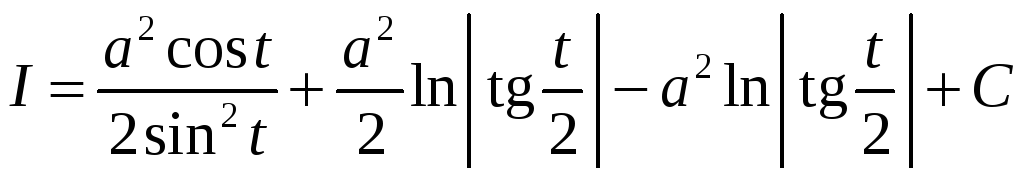
Вернемся к прежней переменной х: , ,

Примеры для самостоятельного решения

1. (замена ), 2. (замена ),

3. (замена ), 4. (замена ),

5. (замена ), 6. (замена ).

Ответы:

1. ,

2. ,

3. ,

4. ,

5. ,

6. .

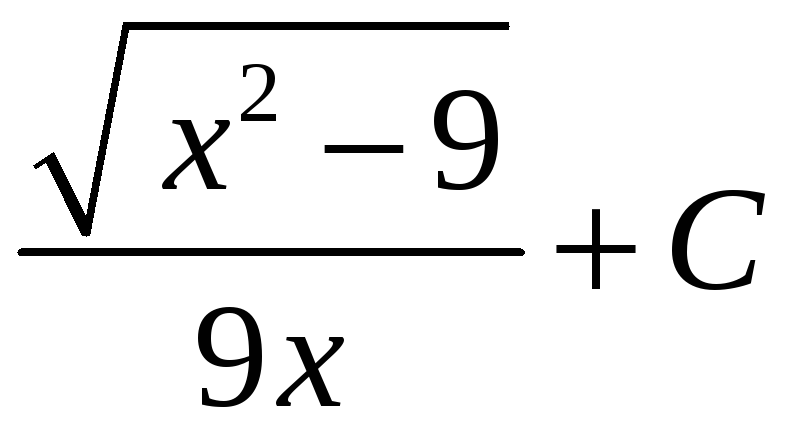Оглавление

3. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ. 1