14. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА

Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области – проекции поверхности на одну из координатных плоскостей.

Если поверхность задана уравнением , то справедлива формула

.

Аналогичные формулы справедливы, если поверхность задана уравнением вида или , тогда

, или

.

Пример 1. Найти площадь части поверхности , вырезанной поверхностью (внутри цилиндра).

Решение. Вычислим площадь поверхности по формуле

.

Найдем по формуле (4.1): .

Тогда .

Проекцией поверхности на плоскость является круг (рис. 1), поэтому для вычисления двойного интеграла перейдем к полярной системе координат:

, ; ;

.

Тогда,

.

Пример 2. Найти массу однородной поверхности , отсекаемой цилиндром и плоскостью (вне цилиндра).

Решение. В данном случае удобно спроецировать поверхность на плоскость , поэтому для вычисления массы поверхности воспользуемся формулой . Тогда

, где .

Вычислим .

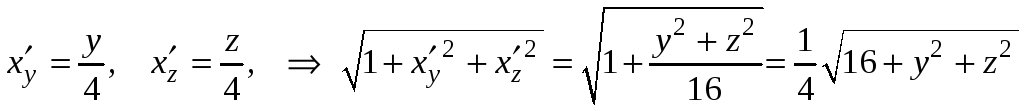Найдем проекцию вырезаемой поверхности на плоскость (рис. 2), исключив переменную из уравнений:

1) (прямые в плоскости );

2) – окружность в плоскости .

Так как проекциями являются прямые и окружность, то при

вычислении двойного интеграла удобно перейти в полярную систему координат: .

Преобразуем уравнения прямых, окружности и подынтегральную функцию:

;

; .

Учитывая, что , имеем:

.

При вычислении интеграла учли, что фигура симметрична относительно начала координат.

Пример 3. Найти положение центра тяжести верхней полусферы , если ее поверхностная плотность в любой точке равна расстоянию от этой точки до оси .

Решение. Так как поверхность симметрична относительно оси и – четная функция относительно и , то ,

, где , ;

.

Проекцией на плоскость является круг, поэтому перейдем к полярным координатам тогда , ,

.

,

.

Тогда . Итак, центр тяжести .

Оглавление

14.ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА 1

Оглавление 5