15. Практическое занятие. Скалярное поле.

Множество точек поля, в которых функция поля принимает постоянное значение , образует поверхность с уравнением , называемую поверхностью уровня поля. Если скалярное поле плоское и находится, например, в плоскости , то его функция поля зависит от двух переменных и , а множество точек, в которых , образуют линию уровня.

Производную поля по направлению вектора можно вычислить по формуле

, где ─ градиент скалярного поля , ─ единичный вектор направления .

Замечания:

1. Скалярное поле в точке быстрее всего возрастает в направлении вектора со скоростью, равной .

2. Скалярное поле 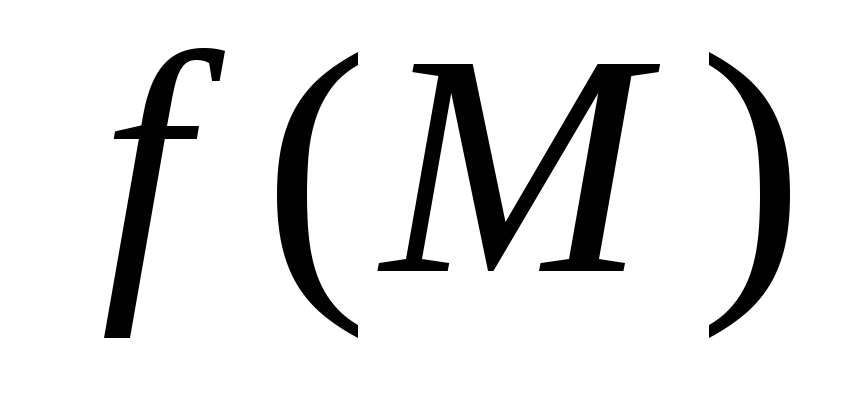в точке быстрее всего убывает в направлении, противоположном вектору , со скоростью, равной .

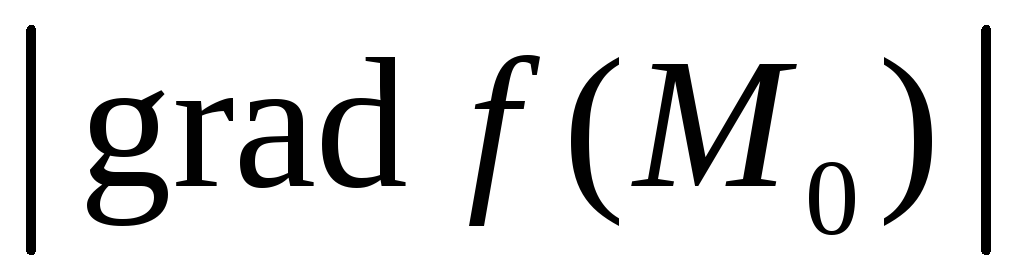3. Вектор 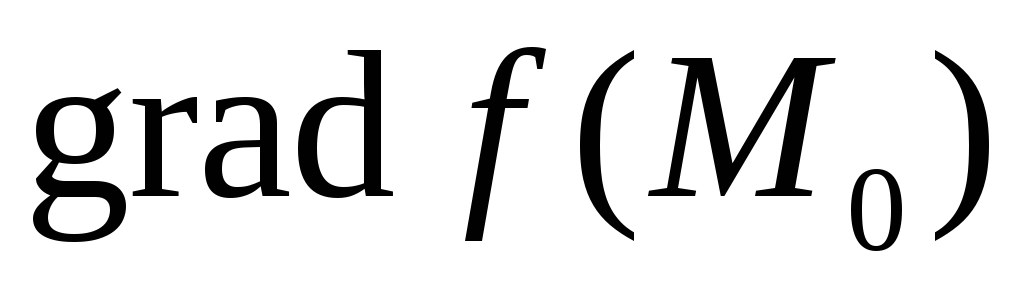направлен по нормали к поверхности уровня поля , проходящей через точку .

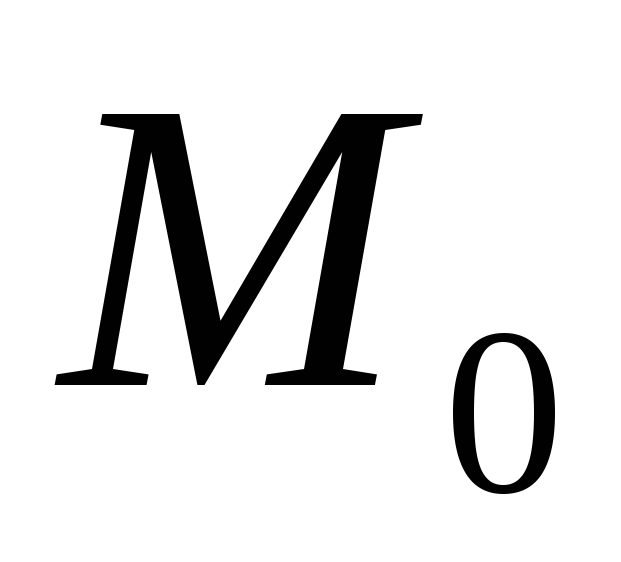Пример 1. Построить линии уровня поля . Найти производную поля в точке в направлении касательной и нормали к линии уровня поля, проходящей через точку .

Решение. Линией уровня называют множество точек, в которых скалярная функция имеет одно и то же значение; в нашем примере . Придадим постоянной различные значения:

а) ; получаем две прямые и ;

б) или – это уравнение эллипса с центром в начале координат; в частном случае при получаем уравнение окружности . Точка принадлежит этой окружности.

в) или – уравнение сопряженной гиперболы (рис. 1).

Для вычисления производной поля по направлению касательной к линии в точке найдем направляющий вектор касательной . Запишем уравнение окружности в векторно-параметрическом виде: . Точке соответствует значение параметра . Вектор коллинеарен направляющему вектору касательной : , ; единичный вектор, направленный вдоль касательной . Запишем , .

По формуле имеем 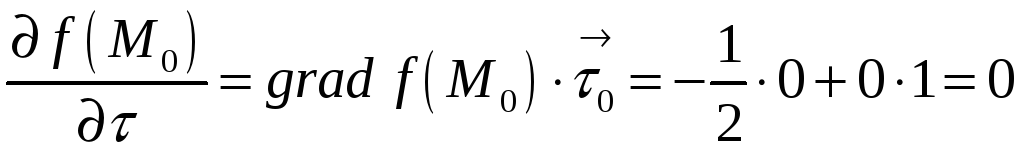, то есть поле по направлению касательной к линии в точке не изменяется.

Направляющий вектор нормали к линии равен , , единичный вектор . Тогда , поле по направлению нормали к линии в точке убывает.

Пример 2. Найти точки, в которых поле по направлению не изменяется.

Решение. Поле в точке не изменяется по направлению , если .

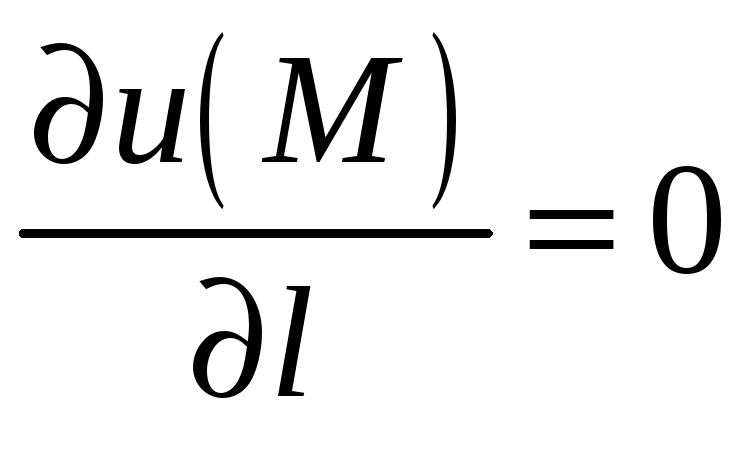Вычислим :

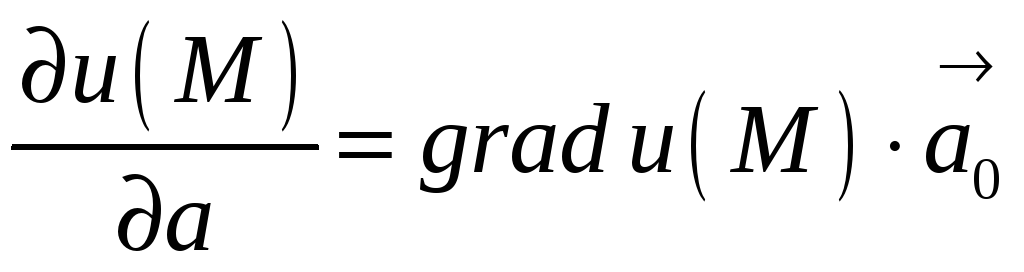, , тогда или .

Итак, в точках плоскости поле по направлению

не изменяется.

Пример 3. Найти производную поля в точке в направлении радиус-вектора этой точки. В каком случае эта производная будет равна ?

Решение. Вычислим и .

Применив формулу , имеем:

.

Итак, .

Рассмотрим случай, когда .

Найдем и, приравняв его , получаем .

Равенство возможно, если : .

Пример 4. Найти , где – постоянный вектор,

– радиус-вектор точки .

Решение. В соответствии с формулой для вычисления скалярного произведения двух векторов , тогда и

. Отсюда следует, что сохраняет во всех точках поля одинаковое направление, совпадающее с направлением вектора , поэтому поверхностями уровня поля являются плоскости с нормальным вектором .

Это утверждение можно получить и непосредственно из определения поверхности уровня .

Пример 5. Показать, что линии уровня полей и ортогональны.

Решение. Угол между линиями измеряется углом между касательными к этим линиям в точке пересечения. Угол между касательными совпадает с углом между нормалями (как углы с соответственно перпендикулярными сторонами). Так как направлен по нормали к линии уровня, то угол между линиями уровня полей , есть угол между и , где – точка пересечения линий уровня.

Вычислим скалярное произведение градиентов:

, следовательно, . Так как – произвольная точка, то линии уровня полей , ортогональны.

Векторные линии векторного поля

Определение. Векторной линией векторного поля называется линия, в каждой точке которой касательный вектор коллинеарен вектору поля.

Для вектора поля система дифференциальных уравнений для отыскания векторных линий имеет вид:

.

Пример 6. Найти векторные линии поля вектора .

Решение. Запишем дифференциальные уравнения векторных линий поля , используя формулу (6.1):

.

При решении задач подобного типа будем пользоваться свойством пропорций:

если , то . Учитывая свойство (6.2), домножим числитель и знаменатель первой дроби на , второй – на , третьей – на и, сложив почленно, получим

.

Отсюда , или (сферы с центром в начале координат радиуса , ).

Теперь запишем систему дифференциальных уравнений в виде или . Домножив равенство на , получим: или (плоскости с нормальным вектором ).

Таким образом, векторные линии данного поля есть линии пересечения сфер с плоскостями:

Пример 7. Найти векторные линии поля градиентов функции

.

Решение. Найдем градиент скалярного поля функции :

.

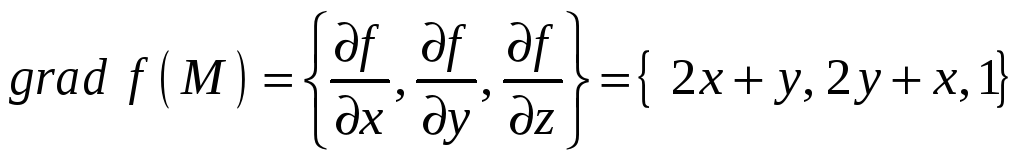Запишем дифференциальные уравнения векторных линий: .

Используя свойство (6.2) пропорций, имеем и .

Проинтегрируем оба равенства:

,

.

Таким образом, векторные линии – линии пересечения поверхностей

Пример 8. Найти векторную линию поля , проходящую через точку .

Решение. Запишем систему дифференциальных уравнений для отыскания

векторных линий: 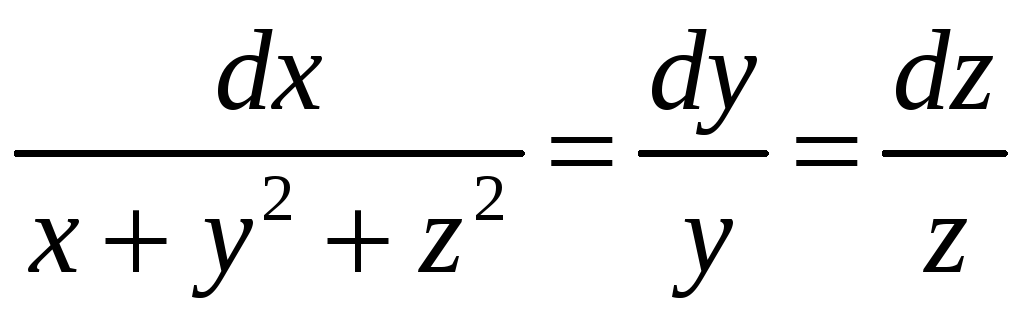. Проинтегрировав дифференциальное уравнение , получим или .

Применив свойство (6.2), запишем систему в виде: или .

Проинтегрировав полученное равенство, имеем

или .

Тогда векторные линии данного поля есть линии пересечения поверхностей

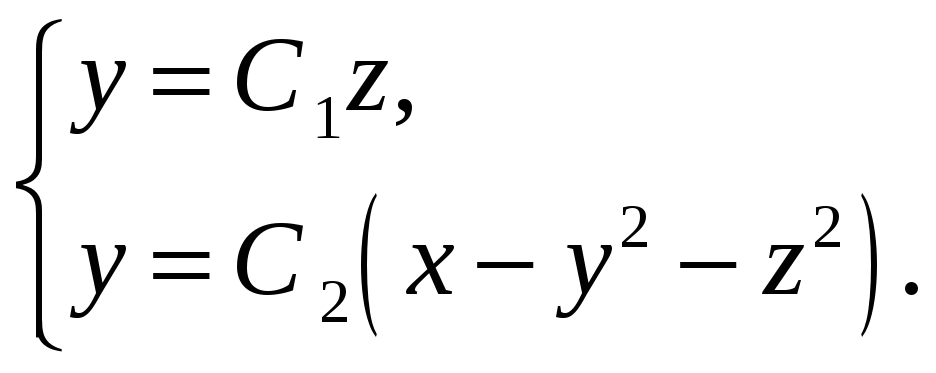
Выделим векторную линию, проходящую через точку . Для этого подставим координаты точки в полученные уравнения поверхностей:

Итак, уравнение искомой векторной линии

Оглавление

15. Практическое занятие. Скалярное поле. 1

Векторные линии векторного поля 6

Оглавление 10