9. Практическое занятие. Геометрические приложения определенного интеграла.

Площадь плоской фигуры

Пример 1. Вычислить площадь фигуры, ограниченной параболой , осью ординат и касательной к параболе в точке .

Решение. Построим заданные линии (рис. 1). Уравнение или определяет параболу с вершиной в точке с осью симметрии, параллельной оси (прямая ). Составим уравнение касательной к параболе в точке . Угловой коэффициент касательной . Уравнение касательной: или . Построим прямую по точкам и . В примере нужно вычислить площадь фигуры . Снизу фигура ограничена параболой , сверху прямой , значения переменной принадлежат отрезку . Для вычисления площади воспользуемся формулой: . Получим:

.

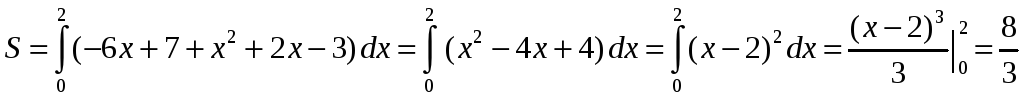Пример 2. Найти площадь фигуры, заключенной между линиями , и осью абсцисс.

Решение. Построим заданные линии и заштрихуем фигуру, площадь которой нужно вычислить (рис. 2). Найдем координаты точки пересечения линий, решив уравнение . Из курса тригонометрии известно, что . Площадь фигуры есть сумма площадей двух фигур:

, где , .

Площадь этой же фигуры можно рассматривать как разность площадей и двух криволинейных трапеций с основаниями на оси , где

, .

Площадь фигуры . Очевидно, что вычислений при решении задачи вторым методом значительно меньше, чем при решении первым.

Примеры для самостоятельного решения

1. Вычислить площадь фигуры, ограниченной линиями

а) , ; б) , . Ответ: а) , б) .

2. Вычислить площадь фигуры, ограниченной кривой , прямой и осью . Ответ: 12.

Объем тела вращения

Пример 3. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями , , вокруг оси .

Решение. Построим линии, ограничивающие фигуру (рис. 3). Это ─ парабола с вершиной в точке и осью симметрии параллельной оси , прямые (ось ), (ось ), прямая , параллельная оси . Объем тела, полученного при вращении фигуры вокруг оси (сечение см. на рис. 5), вычислим по формуле

.

Получим .

Пример 4. Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , .

Решение. Построим линии, ограничивающие фигуру (рис. 4). Для вычисления объема тела вращения непосредственно воспользоваться формулой нельзя, т.к. снизу фигура ограничена не осью , а прямой . Объем тела вращения будет равен разности объемов и , где есть объем тела вращения вокруг оси фигуры, ограниченной линиями объем цилиндра радиусом и высотой . Вычислим и :

.

Здесь мы воспользовались тем, что как интеграл от четной функции, как интеграл от нечетной функции,

Тогда

.

Пример 5. Вычислить объем тела, полученного при вращении вокруг оси криволинейной трапеции, ограниченной осью абсцисс, прямыми и кривой (рис.5).

Решение. Объем тела вращения где объем цилиндра радиусом и высотой , , объем тела, полученного при вращении вокруг оси криволинейного треугольника, ограниченного линией , прямыми . Объем вычислим по формуле . Из уравнения найдем . Тогда

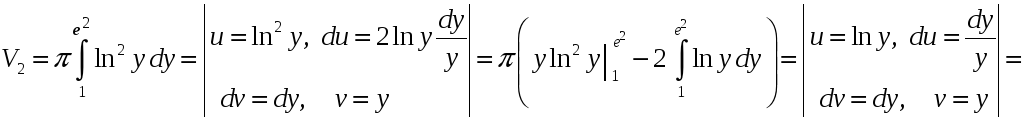
Объем тела вращения первоначальной криволинейной трапеции вокруг оси :

.

Примеры для самостоятельного решения

1. Фигура, ограниченная эллипсом 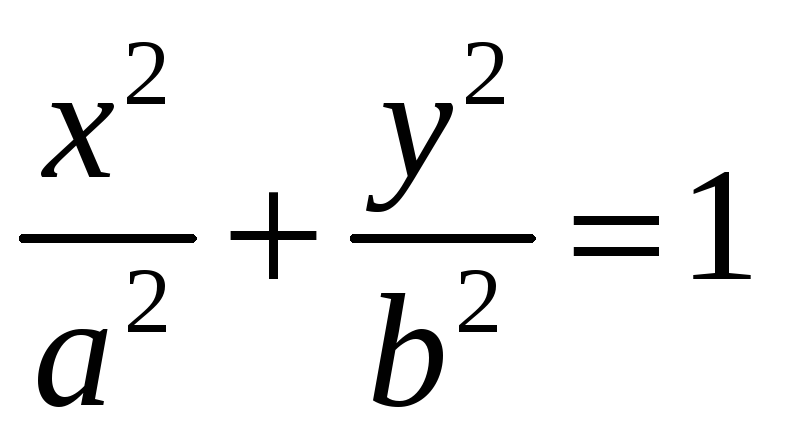, вращается а) вокруг оси , б) вокруг оси . Найти объемы получающихся эллипсоидов вращения.

Ответ: а) ; б) .

Пример 6. Вычислить длину дуги кривой , .

Решение. Длину дуги кривой вычислим по формуле

.

Воспользуемся четностью функции :

.

Пример 7. Вычислить длину дуги кривой .

Решение. Кривая задана уравнением , поэтому длину дуги кривой вычислим по формуле

Пример 8. Вычислить длину одной арки циклоиды

Решение. Уравнение кривой задано параметрическими уравнениями, поэтому длину кривой вычислим по формуле В нашем случае

,

Здесь мы учли, что , т.к. . Тогда

Пример 9. Найти длину дуги кривой

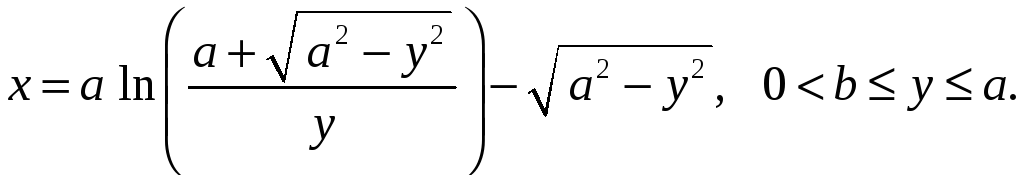
Решение. Кривая задана уравнением , поэтому длину дуги кривой вычислим по формуле . Вычислим и :

, после преобразований ,

.

Тогда .

Пример 10. Вычислить длину дуги линии от начала координат до ближайшей точки с вертикальной касательной.

Решение. Кривая задана параметрическими уравнениями, поэтому

.

Вычислим:

, , .

Найдем значения параметра, соответствующее началу координат и точке с ближайшей к нему вертикальной касательной. В начале координат , , что возможно при . Угловой коэффициент вертикальной касательной равен бесконечности:

, . Тогда .

Примеры для самостоятельного решения

1. Вычислить длину дуги полукубической параболы , заключенной между точками . Ответ: .

2. Вычислить длину астроиды . Ответ: .

Указание: воспользоваться симметрией линии и вычислить сначала длину части дуги, расположенной в первой четверти.

Оглавление

9. Практическое занятие. Геометрические приложения определенного интеграла. 1

Площадь плоской фигуры 1

Примеры для самостоятельного решения 2

Объем тела вращения 2

Примеры для самостоятельного решения 4

Примеры для самостоятельного решения 6

Оглавление 7