11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ДВОЙНОЙ ИНТЕГРАЛ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ.

Пусть область в плоскости ограничена линиями , , , . Тогда

Чтобы вычислить данный интеграл, необходимо:

1) построить область интегрирования;

2) записать двойной интеграл через повторный; в повторном интеграле сначала расставить внутренние пределы интегрирования, т.е. пределы изменения . Для этого на чертеже нужно двигаться параллельно оси . При этом мы войдем в фигуру через линию, на которой , а выйдем через линию, на которой , т.е. переменная интегрирования меняется от до ;

3) проецируя область на ось , расставить внешние пределы интегрирования (это всегда – числа, а не функции);

4) вычислить сначала внутренний интеграл при постоянном затем – внешний интеграл.

Пусть область в плоскости ограничена линиями , , , . Тогда

Пример 1. Расставить пределы интегрирования в том и другом порядке в интеграле , если область интегрирования – круговой сектор OAB , где , , .

Решение. Обозначим .

Запишем уравнения линий, ограничивающих область . Прямая () задается уравнением , прямая () – уравнением ,

дуга – часть окружности с уравнением .

1). Из уравнения окружности выразим : , так как .

При переходе от двойного интеграла к повторному сначала расставляют внутренние пределы интегрирования («от линии до линии»), а затем – внешние («от точки до точки»). Так как снизу область ограничена двумя линиями (рис. 2), то при расстановке пределов интегрирования придется разбить данный интеграл на два интеграла, пользуясь свойством аддитивности: .

Область снизу ограничена линией , сверху – линией , причем .

Область снизу ограничена линией , сверху – линией , причем .

Таким образом, .

2). Запишем теперь повторный интеграл, сменив порядок интегрирования. Слева область ограничена двумя линиями: отрезком ( ) и дугой . Справа область также ограничена двумя линиями: отрезком () и дугой . Поэтому разобьем интеграл на два интеграла.

По свойству аддитивности .

Область слева ограничена линией , справа – линией ,

причем . Область слева ограничена линией , справа – линией , причем .

Таким образом, снова получаем два повторных интеграла:

.

Пример 2. Изменить порядок интегрирования в интегралах:

а) ; б) .

Решение. а). Рассмотрим область интегрирования . Сверху она ограничена линией , снизу – линией , где (рис. 2).

Изменим порядок интегрирования. Уравнения граничных линий разрешим относительно . Слева область ограничена линией , справа – линией , где . Тогда

.

б). Построим область интегрирования . Она ограничена линиями , , , . Слева область ограничена линией . Преобразуем это уравнение: или Это уравнение определяет часть окружности с центром в точке и радиусом .

Справа область ограничена прямой .

Изменим порядок интегрирования. Для этого уравнения граничных линий разрешим относительно . Снизу область интегрирования ограничена одной линией , но сверху имеем две граничные линии: при и при (рис. 3), поэтому в результате получим сумму двух повторных интегралов, то есть

.

Пример 3. Найти площадь области , ограниченной линиями

, , .

Решение. Для вычисления площади данной фигуры воспользуемся формулой

.

По аналогии с предыдущими примерами расставим пределы интегрирования в повторном интеграле. Для этого построим область (рис. 4), предварительно отыскав точки пересечения кривых: .

Тогда , то есть

.

Пример 4. Вычислить , если область ограничена линиями .

Решение. Построим данную область (рис. 5). В данном случае порядок интегрирования будем выбирать, учитывая не область интегрирования (она достаточно простая), а подынтегральную функцию, чтобы упростить вычисления при интегрировании.

При вычислении интеграла придется дважды воспользоваться формулой интегрирования по частям, что не очень удобно. Поэтому сначала вычислим интеграл .

Итак,

.

Пример 5. Найти статический момент однородного круга относительно его касательной.

Решение. Введем систему координат таким образом, чтобы одна из координатных осей являлась касательной к кругу (рис. 7). Например, центр круга расположим в точке с координатами , где – радиус круга. Тогда ось будет касательной. Уравнение соответствующей окружности имеет вид: .

Теперь наша задача – найти статический момент круга относительно оси . Для этого воспользуемся формулой , где  – поверхностная плотность. Так как фигура однородная, то и .

При расстановке пределов интегрирования воспользуемся тем, что верхняя часть окружности задается уравнением , нижняя часть – уравнением , где . Поэтому имеем:

.

При вычислении последнего интеграла воспользовались геометрическим смыслом определенного интеграла.

Пример 6. Вычислить среднее значение функции в области , ограниченной линиями .

Решение. Вычислим среднее значение функции по формуле , где – площадь области .

Точки пересечения линий :

, (рис.7).

Тогда ;

.

Воспользовались тем, что интеграл от нечетной функции по отрезку равен нулю, а от четной функции .

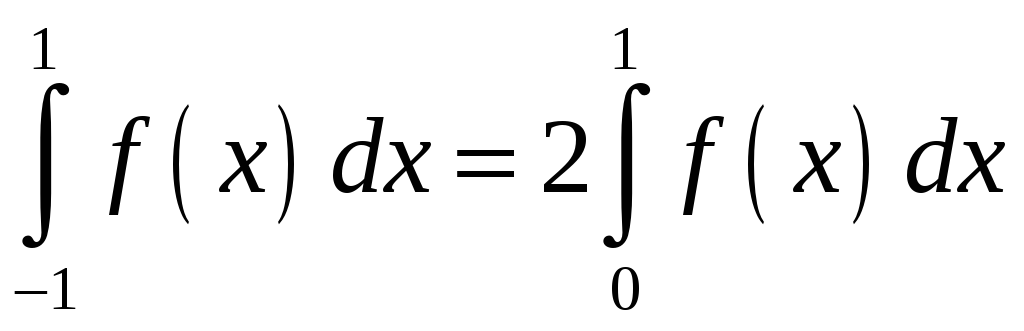Оглавление

11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ДВОЙНОЙ ИНТЕГРАЛ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ. 1

Оглавление 7