8. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

Основная формула для вычисления определенного интеграла ─ формула Ньютона-Лейбница

, где ─ первообразная для функции

При вычислении определенного интеграла следует учитывать следующие полезные свойства:

если функция − нечетная на отрезке , то ;

если функция − четная на , то ;

если функция имеет период T, то .

Основные методы (как и при вычислении неопределенного интеграла) ─ метод интегрирования по частям и метод замены переменной.

Пусть − дифференцируемые функции. Тогда

.

Это ─ формула интегрирования по частям для определенного интеграла.

Рекомендации по применению этой формулы такие же, как для неопределенного интеграла.

При замене переменной в определенном интеграле следует:

1) заменить переменную на удачно подобранную функцию ;

2) заменить на ;

3) заменить отрезок изменения переменной x на отрезок изменения переменной t, найдя и из условий ;

4) вычислить получившийся определенный интеграл.

Таким образом,

Отметим, что при вычислении определенного интеграла по этой формуле не надо возвращаться к первоначальной переменной, как это приходилось делать при замене переменной в неопределенном интеграле. Рекомендации по выбору новой переменной такие же, как и для неопределенного интеграла.

Пример 1. Вычислить интегралы: , ,

, , .

Решение. 1). Рассмотрим интеграл . Используя свойства интеграла и формулу Ньютона-Лейбница, получим:

.

2). В интеграле подынтегральная функция является нечетной на отрезке (проверьте, что ), следовательно, интеграл равен нулю.

3). В интеграле умножим числитель и знаменатель на . Тогда

4). В интеграле подынтегральная функция является периодической с периодом . Воспользуемся тем, что

( ─ период функции ). Представим интеграл в виде суммы интегралов:

.

Вычислим интеграл

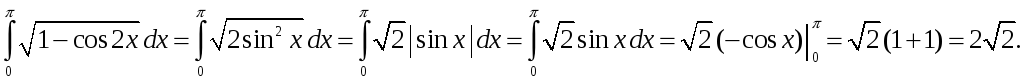Итак, .

Пример 2. Вычислить интегралы: , .

Решение. Интегралы вычислим методом интегрирования по частям:

.

1). Для вычисления интеграла положим , . Тогда , . По формуле интегрирования по частям имеем:

2). При вычислении интеграла положим . Тогда

,

.

Заметим, что если положить то мы не сможем найти , так как интеграл «неберущийся».

Пример 3. Вычислить интегралы: ; .

Решение. Для вычисления интегралов применим метод замены переменной в определенном интеграле.

1). Для вычисления интеграла сделаем замену переменной , найдем и новые пределы интегрирования (пределы изменения переменной ): . Получим:

2). Для вычисления интеграла сделаем замену переменной или , найдем и новые пределы интегрирования (пределы изменения переменной ): . Получим

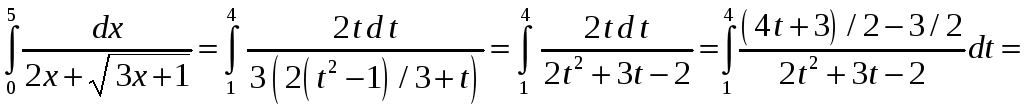
Пример 4. Вычислить интеграл .

Решение. При вычислении интеграла воспользуемся утверждениями:

─ для нечетной функции, ─ для четной функции.

Функция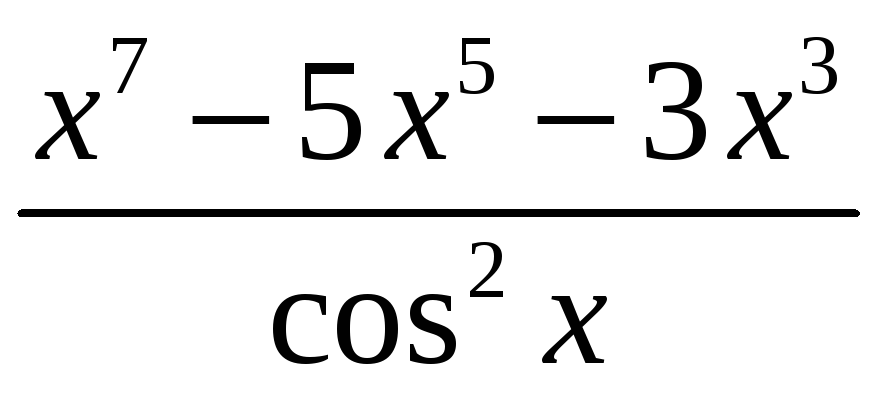 является нечетной на и .

Функция является четной на , поэтому

.

Примеры для самостоятельного решения

1. Вычислить: , , , ,

, , , , .

Ответы:

, , , ,

, , , , .

2. Доказать равенства:

а) ; б) ; в) .

В примере 2.б) использовать свойство: , если .

Оглавление

8. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. 1

Примеры для самостоятельного решения 5

Ответы: 5

Оглавление 6