10. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ  РОДА.

Если кривая AB задана параметрическими уравнениями , где , – непрерывно дифференцируемые функции, то справедлива формула

.

Если плоская кривая задана уравнением , , то справедлива формула

.

Если плоская кривая задана уравнением , то справедлива формула

.

Пример 1. Найти момент инерции относительно участка однородной линии от точки до точки .

Решение. Применим формулу . Линия задана уравнением , поэтому и .

Пример 2. Найти массу части дуги , отсеченной дугой , если поверхностная плотность .

Решение. Вычислим массу по формуле .

Найдем координаты точек пересечения данных линий.

Для этого решим систему уравнений:

Откуда .

Таким образом, получили две точки: и (рис. 1).

Уравнение дуги AB запишем в виде или .

Так как , воспользуемся формулой:

;

.

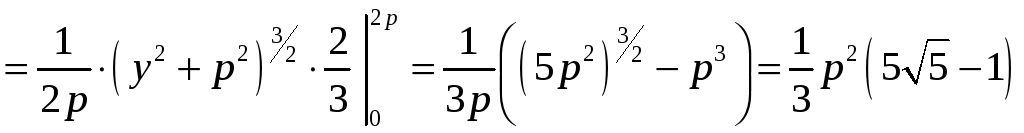Пример 3. Найти момент инерции относительно начала координат однородной линии

Решение. Момент инерции относительно начала координат найдем по формуле:

.

Линия (L) – линия пересечения сферы и плоскости . Подставив в уравнение сферы вместо , получим уравнение линии (L) в виде:

или

Запишем уравнение линии в виде или .

Тогда .

Итак, .

Пример 4. Вычислить длину кривой , заданной параметрическими уравнениями при .

Решение. Длину дуги кривой можно вычислить по формуле .

Кривая задана параметрическими уравнениями при , поэтому по формуле имеем

и .

Оглавление

10. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ  РОДА. 1

Оглавление 4