Математика ЗО от Белоусовой / Математический анализ, практика 2 семестр / Практика 4
.doc4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
При нахождении интегралов с помощью
тригонометрических подстановок обычно
приходят к интегралам от функций вида
.
Рассмотрим интегрирование таких функций
более подробно.
Случай 1.
,
где (или )
– положительное нечётное число.
В этом случае следует отделить от
нечетной степени
(или
)
одну степень и подвести ее под знак
дифференциала.
Пример 1. Найти
.
Решение. Подынтегральная функция
содержит
в нечетной степени, поэтому отделим
и воспользуемся тем, что
,
а
.
Тогда
.
Пример 2. Найти
.
Решение. Подынтегральная функция
содержит
в нечетной степени, поэтому отделим
и воспользуемся тем, что
,
а
.
Тогда
.
Случай 2.
,
где
и –
четные неотрицательные числа. В
этом случае следует понизить степень,
используя следующие формулы:
,
,
.
Пример 3. Найти
.
Решение.
.
Пример 4. Найти
.
Решение.
.
Случай 3.
,
где
и –
целые числа и хотя бы одно из них
отрицательное.
Здесь единой рекомендации нет. Выделим несколько случаев.
В подынтегральной функции степень числителя четная и на единицу меньше степени знаменателя. В этом случае применяется метод интегрирования по частям (см. пример 7.4).
В подынтегральной функции степень
числителя на две единицы меньше степени
знаменателя. Такие интегралы сводятся
к
или
.
Если степень числителя нечетная, то имеем случай 1).
Пример 5. Найти
.
Решение.
.
В подынтегральной функции степень
числителя меньше степени знаменателя
на
(
>2).
Следует увеличить степень числителя,
умножив его на выражение
,
равное единице.
Пример 6. Найти
.
Решение.
.
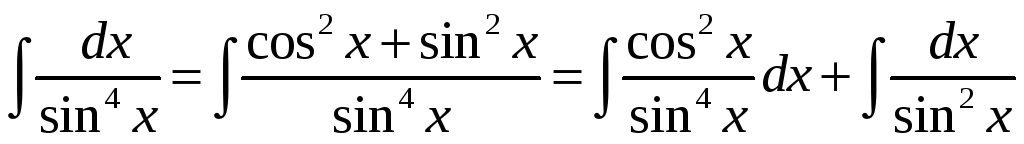
В подынтегральной функции степень
числителя больше или равна степени
знаменателя. Следует в числителе
заменить на
,
а
заменить на
.
Пример 7. Найти
.
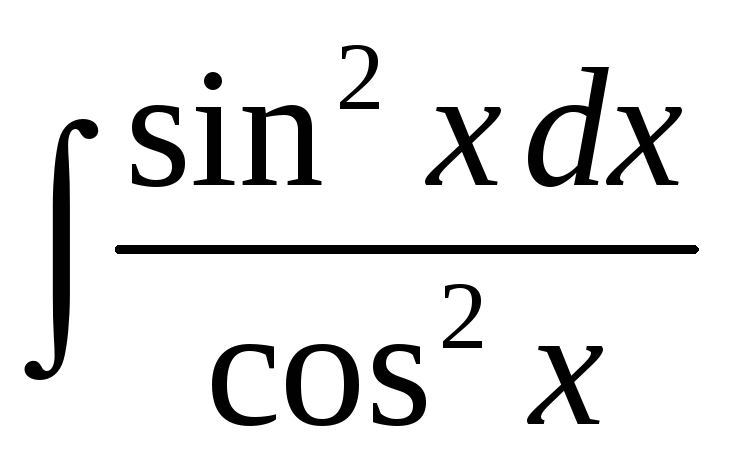Решение.
.
Случай 4.
,
где
− рациональная функция от
:
а) если
,
то следует подынтегральное выражение
выразить через
и
,
б) в остальных случаях (не рассмотренных
ранее) следует подынтегральное выражение
выразить через
и
.
Пример 8. Вычислить интегралы:
1)
;
2)
.
Решение. 1)
,
поэтому подынтегральное выражение
выразим через
и
:
2).
.
Здесь подынтегральное выражение удобнее
выразить через
и
:
Пример 9. Найти интеграл
.
Решение. Так как
,
то следует подынтегральное выражение
выразить через
и
:
Примеры для самостоятельного решения
Найти интегралы:
1.
,
2.
,
3.
,
4.
,
5.
,
6.
,
7.
,
8.
.
Ответы. 1.
,
2.
,
3.
,
4.
,
5.
,
6.
.
7.
,
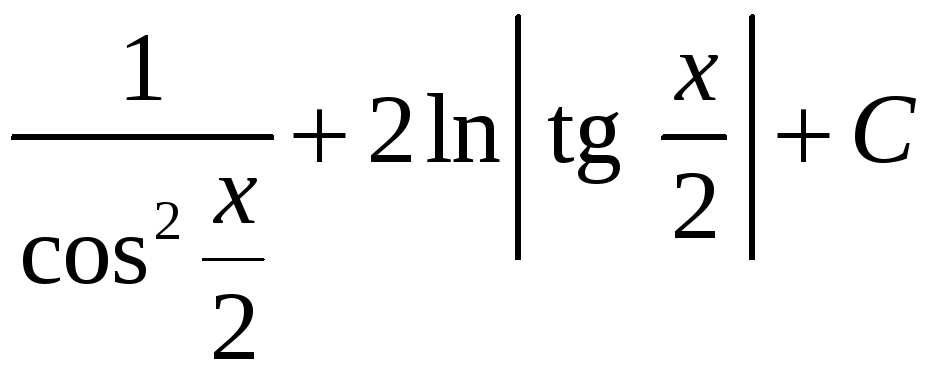8.
.
Оглавление
4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ. 1
Примеры для самостоятельного решения 4
Оглавление 5