Математика ЗО от Белоусовой / Алгебра и геометрия и ТДУ / Лекции по АГиТДУ / Лекция 11

Лекция 11. Кольцо многочленов. Свойства конечных сумм

Сумму конечного числа слагаемых коротко можно обозначить символом , т.е. (i называется индексом суммирования или немым индексом).

Свойство 1. Сумма не зависит от обозначения немого индекса, т.е.

.

Свойство 2.(Однородность)

(множитель, стоящий под знаком  и не зависящий от индекса суммирования можно вынести за знак ).

Свойство 3. (Аддитивность)

.

Свойство 4.

.

При суммировании по двум индексам можно изменить порядок суммирования.

Пусть задано произвольное числовое поле . Рассмотрим множество многочленов, т.е. функций вида

зависящих от аргумента , принимающего значения из поля , и имеющих коэффициенты . Будем считать многочлен многочленом степени n, если , и обозначать . Единственным многочленом , не имеющим определенной степени, является многочлен, у которого все коэффициенты равны нулю. Мы будем называть его нулевым многочленом и обозначать символом 0.

Равенство многочленов

Пусть

.

.

Это определение равенства многочленов – формально-алгебраическое.

На многочлены можно смотреть, как на функции.

С этой точки зрения дадим второе определение равенства многочленов:

.

Эти определения эквивалентны.

Определим для многочленов операции сложения и умножения.

Пусть и предположим для определенности, что . Тогда

т.е. коэффициенты есть сумма произведений тех коэффициентов многочленов и , сумма индексов которых равна k.

Например, ; ; и т.д.

Частным случаем произведения многочленов является произведение многочлена на число , так как ненулевое число можно рассматривать как многочлен нулевой степени.

Множество многочленов с введенными выше операциями представляет собой коммутативное кольцо. (Проверить все аксиомы кольца самим!) Кольцо многочленов будем обозначать . Но не является полем, так как для умножения многочленов обратная операция – деление – не существует.

Заметим, что в существует единица, ее роль играет нулевой многочлен .

В этом отношении кольцо многочленов напоминает кольцо целых чисел. Эта аналогия проявляется и в том, что для многочленов, как и для целых чисел, имеет место алгоритм деления с остатком (алгоритм Евклида).

Теорема (об алгоритме Евклида)

Для любых многочленов и , nm, можно найти единственные многочлены и , такие, что , причем степень меньше степени или же ; – называется остатком.

Проиллюстрируем алгоритм Евклида на конкретном примере:

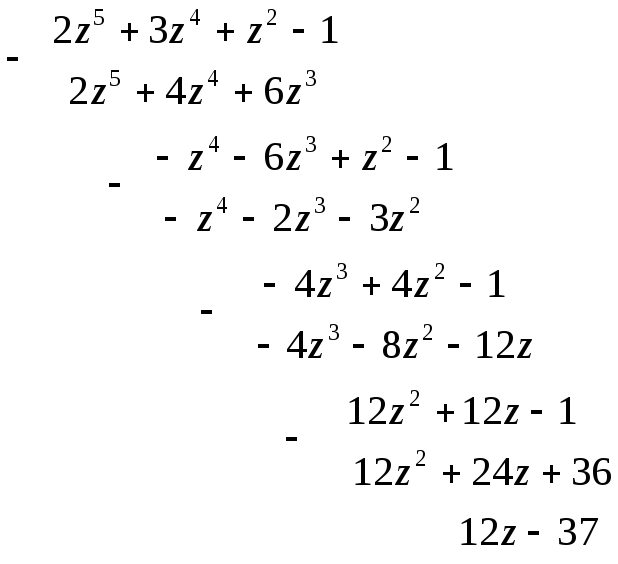
Т.о. для двух многочленов и (применяя указанный алгоритм) указали два многочлена и таких, что

. (Проверить справедливость равенства самостоятельно).

Теорема Безу

При делении многочлена степени (n1) на разность z-a получается остаток, равный .

Доказательство. При делении многочлена на многочлен первой степени, получается остаток r- многочлен, степень, которого меньше 1, т.е. многочлен нулевой степени (число). По предыдущей теореме имеем равенство , которое верно для любого z, в частности, и для z=a, т.е. .

Определение. Корнем многочлена (ненулевой степени) называется такое значение z, при котором многочлен обращается в ноль.

Следствие из теоремы Безу.

( делится на )  (- корень ), т.е. имеет место равенство.

Замечание. Равенство , называется алгебраическим уравнением степени n. Корень многочлена есть корень уравнения .

Естественно возникает вопрос: всякое ли алгебраическое уравнение степени n>0 имеет корни? Ответ на этот вопрос дает основная теорема алгебры.

Теорема Гаусса

(дается без доказательства)

Всякое алгебраическое уравнение степени n>0 над полем С комплексных чисел имеет хотя бы один корень.

Следствия из основной теоремы.

Теорема (о разложении многочлена на линейные множители)

Всякий многочлен степени n>0 над полем C может быть разложен на линейные множители. Это разложение единственное с точностью до перестановки сомножителей местами.

Доказательство. Множитель степени n1 над полем C (т.е. с комплексными коэффициентами) имеет хотя бы один корень . Поэтому имеет место разложение:

, где - многочлен степени (n-1). Этот многочлен над полем C имеет хотя бы один корень (если n2) и , откуда следует, что . Продолжая этот процесс, мы получим разложение многочлена в произведение линейных множителей .

Среди чисел могут быть равные между собой числа. Предположим для простоты, что попарно различны, а каждое из чисел равно одному из первых. Тогда многочлен можно записать в таком виде: , где при и . Это разложение называется каноническим разложением многочленана множители.

Если в каноническом разложении f(z), то корень называется простым; если же , то корень называется кратным. Число называется кратностью корня.

Теперь мы можем сделать весьма важный вывод:

любой многочлен степени n>0 над полем С имеет n корней, если каждый из корней считать столько раз, какова его кратность.

Например,

; ; ; .

Разложение многочлена над полем R

Лемма. Если с действительными коэффициентами имеет комплексный корень , то является также корнем ; т.е. .

Пусть . Тогда .

Найдем значение .

.

Здесь были применены свойства комплексно-сопряженных чисел:

, , если R. Из этой леммы следует, что в разложение многочлена с вещественными коэффициентами комплексные корни входят попарно сопряженными. Перемножив линейные множители, соответствующие паре комплексно-сопряженных корней , получим квадратный трехчлен вида с вещественными коэффициентами, т.к. R, .

После обозначения ; квадратный трехчлен примет вид , R.

Имеет место следующая теорема.

Теорема (о разложении многочлена над полем R)

Многочлен с вещественными коэффициентами степени n2 может быть разложен на вещественные множители первой и второй степени соответствующей кратности. Это разложение единственное с точностью до перестановки множителей местами.

,

при этом .

Например,,,

.