Математика ЗО от Белоусовой / Алгебра и геометрия и ТДУ / Лекции по АГиТДУ / Лекция 13

Лекция 13. Обращение матриц. Определители порядка n

Обращение матриц

Пусть  квадратная матрица порядка n. Матрица называется обратной к , если(ясно, чтоматрица порядка n и она единственная с этим свойством).

Матрица, обратная к матрице, обозначается через.

Если матрицаимеет обратную, то называется обратимой.

Свойства операции обращения

.,

. ,

.,

..

Докажем, например, свойство . ;

.

Из единственности обратной матрицы получаем равенство.

Замечание 1. Для обратимой матрицы можно рассмотреть отрицательную степень:,.

Замечание 2. Пусть и – матричные уравнения, где  обратимая матрица,  неизвестная матрица. Тогда решением первого уравнения является матрица, второго  матрица.

Как определить обратима ли матрица? Если она обратима, то как найти обратную к ней матрицу?

Ответим на эти вопросы после введения понятия определителя (детерминанта) матрицы порядка n.

Определители n-го порядка

Для того чтобы ввести понятие определителя матрицы порядка n, нам понадобятся некоторые сведения о перестановках.

Определение (перестановки).

Пусть дано n натуральных чисел 1,2,…,n. Перестановкой из n натуральных чисел 1,2,…,n называется расположение этих чисел в определенном порядке.

(1,2,…,n)  естественная перестановка,

()  произвольная перестановка.

Например, найти все перестановки из чисел 1,2,3.

Всевозможных перестановок из этих чисел будет 6=3!:(1,2,3), (2,1,3), (3,2,1), (2,3,1), (3,1,2),(1,3,2).

Лемма ( о количестве перестановок из n чисел).

Число всевозможных перестановок из n чисел равно n!= n.

Инверсия. Говорят, что два числа в перестановке образуют инверсию (беспорядок), если большее число стоит перед меньшим.

Например, в перестановке (1,4,3,5,2) инверсии образуют следующие пары: (4,3), (4,2), (3,2), (5,2). Итак, в рассматриваемой перестановке четыре пары чисел образуют инверсии, т.е. число инверсий в перестановке (1,4,3,5,2) равно 4 .

Число инверсий в перестановке () будем обозначать через . Итак, (1,4,3,5,2)= 4. Легко заметить, что , где  число чисел, стоящих перед числом в перестановке, полученной из данной вычеркиванием чисел, меньших числа (если таковы имеются)

.

Определение. Перестановка называется четной, если суммарное количество инверсий в перестановке – четное число и нечетной  нечетное число.

Определение определителя порядка n (n2).

Пусть дана матрица над числовым полем P.

Определителем порядка n называется число, полученное из элементов данной матрицы по следующему правилу:

а) это алгебраическая сумма n! слагаемых (членов определителя);

б) каждый член определителя представляет собой произведение n элементов матрицы А, взятых по одному из каждой строки и каждого столбца;

в) каждому члену определителя приписывается знак «+», если эта перестановка нечетная, при условии, что первые индексы элементов произведения расположены в естественном порядке.

Обозначение определителя порядка n:

.

Итак, по определению,

.

Замечание. Это определение распространяется и на определители второго и третьего порядков. (Проверить самостоятельно)

Все свойства определителей второго и третьего порядков (см. лекцию 1) переносятся на определители порядка n>3.

Можно добавить к ним еще следующие свойства определителей:

1⁰. , т.е. определители матриц перемножаются по тому же правилу, что и сами матрицы.

Например, .

.

, , .

2⁰. , .

3⁰. (это обобщение первого свойства определителей второго и третьего порядков)

Основные способы вычисления определителей порядка n

Укажем некоторые способы вычисления определителя.

1. По определению (например, вычисление определителей второго и третьего порядков).

2. По формуле разложения

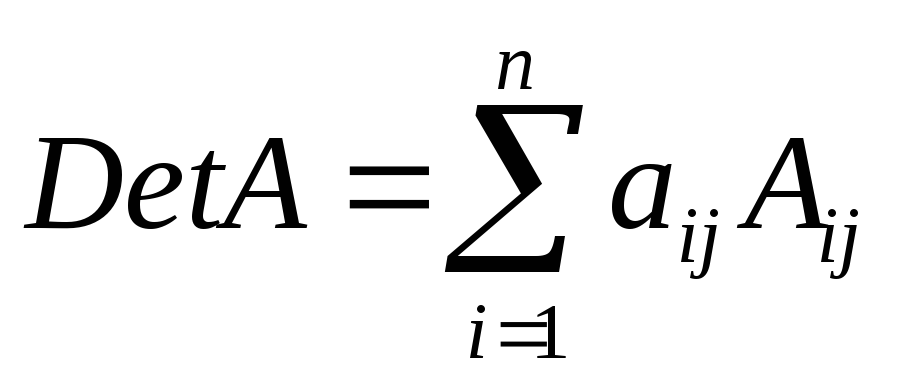3. (формула разложения определителя по элементам j-го столбца).

4. (формула разложения определителя по элементам i-й строки).

5. Приведение определителя к треугольному виду (не изменяя его величены), т.е. к виду

.

Тогда .

Пример. Вычислить определитель порядка n

.

Прибавив к элементам первого столбца определителя соответ-ствующие элементы второго, третьего и т.д. n-го столбца (от чего величина определителя не изменится), получим определитель вида:

Далее, к элементам второй, третьей и т.д. n-й строк прибавим соответствующие элементы первой строки, предварительно умноженные на (-1). Получим определитель треугольного вида.

.

Обращение матриц

Теорема обращения. Для того чтобы матрица A имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Дано: .

Требуется доказать: .

Доказательство. .

.

Дано: .

Требуется доказать: .

Доказательство. Для каждого элемента матрицы найдем алгебраическое дополнение A_ij и составим матрицу, элементами которой будут числа A_ij, т.е. , затем эту матрицу протранспонируем. Получим матрицу , где . называется присоединенной матрицей к матрице А.

Вычислим и

Итак,

Аналогичным путем устанавливается, что .

Т.к. по условию теоремы , то .

. Этими равенствами устанавливается факт существования обратной матрицы для матрицы А.

Таким образом, .

Теорема доказана.

Замечание. Из теоремы следует формула для вычисления обратной матрицы, которая носит название формулы обращения матрицы.

Например: . Найти А^-1.

В начале установим факт существования А^-1. Для этого вычислим

. Так как , то

.

Решение линейных систем по формулам Крамера

Пусть дана система n линейных уравнений с n неизвестными (СЛУ) над произвольным числовым полем . Запишем ее в матричном виде , где , .

A – основная матрица СЛУ, обозначим символом . Если , то СЛУ называется невырожденной, если , то –вырожденной.

Решим вопрос о совместности СЛУ Ax=B.

Система Ax=B называется совместной, если имеет хотя бы одно решение, в противоположном случае она называется несовместной. Если каждое из уравнений линейной системы обращается в верное равенство в поле P после замены неизвестных x_i числами , то набор чисел называется решением системы Ax=B, а компонентой решения.

Теорема Крамера. Если СЛУ Ax=B – невырожденная система, то она совместна и ее единственное решение находится по формулам Крамера:

, где -определитель матрицы, полученной из матрицы А путем замены ее j-го столбца столбцом свободных членов системы.

Доказательство. Так как

и матричное уравнение Ax=B имеет единственное решение .

.

Или в развернутом виде:

.

Отсюда , (*)

где - определитель матрицы, полученной из матрицы А заменой ее j-го столбца столбцом свободных членов.

Формулы (*) носят название формул Крамера.

Пример.Решить линейную систему

;

.

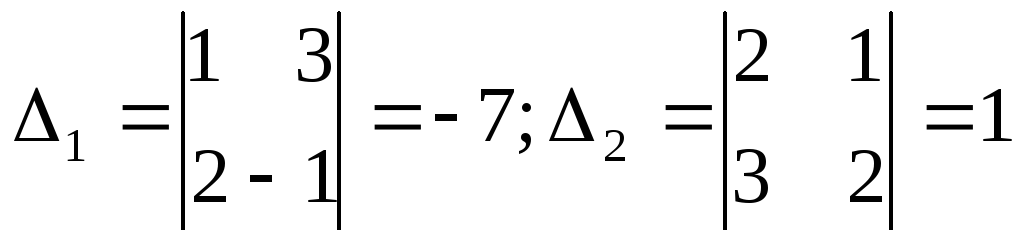Пусть линейная система имеет вид: - однородная система линейных уравнений (ОСЛУ)

Пусть .

Система всегда совместна ( - решение системы всегда!)

Если , то по теореме Крамера ОСЛУ имеет единственное (тривиальное, т.е. ) решение.

Имеет место теорема: для того чтобы ОСЛУ имела ненулевое решение, необходимо и достаточно, чтобы определить системы был равен нулю.

Теорему доказать самостоятельно.

Замечание. Решение СЛУ по формулам Крамера достаточно трудоемко. На практике более удобным и более общим методом решения линейных систем является метод Гаусса, который будет изложен на следующей лекции.