Математика ЗО от Белоусовой / Алгебра и геометрия и ТДУ / Лекции по АГиТДУ / Лекция 7
.docЛекция 7. Элементы аналитической геометрии на плоскости R2
1.Уравнение линии в R2 и понятие об уравнении прямой
Предположим, что на плоскости R2 заданы:
-
прямоугольная система координат Оху;
-
некоторая линия (l) (эта линия называется плоской).
Рассмотрим некоторое уравнение, связывающее две переменные величины х и у: F(x,y)=0.
Определение. Уравнение F(x,y)=0 называется уравнением линии (l) (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии (l), и не удовлетворяют координаты х и у точек, не лежащих на линии (l).
С точки зрения этого определения сама линия (l) представляет собой (в заданной системе координат) множество точек, координаты которых удовлетворяют уравнению F(x,y)=0.
Параметрическое представление линии
Для аналитического представления линии (l) часто бывает удобно выражать переменные координаты х и у точек этой линии при помощи третьей вспомогательной переменной (или параметра) t: х=х(t), y=y(t), где х(t), y(t) – функции от t, tТ (аналогично параметрическому представлению линии (l) в R3). Исключая (если возможно) из параметри-ческих уравнений линии (l) параметр t, придем к уравнению F(x,y)=0.
Прямая на плоскости R2
При переходе от пространства R3 к плоскости R2 получим общее уравнение прямой: Ax+By+C=0 (A2+B20),
каноническое
уравнение прямой:
![]() ,
,
параметрические
уравнения прямой:
![]() .
.
И з
канонического уравнения прямой можно
получить уравнение
з
канонического уравнения прямой можно
получить уравнение
![]() ,
или
,
или
![]() ,
,
где
![]() - угловой коэффициент прямой (рис. 15).
- угловой коэффициент прямой (рис. 15).
Разрешив последнее
уравнение относи-тельно у и обозначив
![]() ,
получим уравнение прямой (l)
в виде y=kx+b
– простейшее уравнение прямой (хорошо
известное из школы). Простейшее уравнение
прямой (l) можно получить
из общего уравнения при условии, что
,
получим уравнение прямой (l)
в виде y=kx+b
– простейшее уравнение прямой (хорошо
известное из школы). Простейшее уравнение
прямой (l) можно получить
из общего уравнения при условии, что
![]() .
.
Угловые соотношения между двумя прямыми
Угол между двумя прямыми можно определить по той же самой формуле, что и угол между прямыми в R3, т.е.

 .
.
Если прямые заданы
простейшими уравнениями, т.е.
![]()
то
![]() .
.
Действительно,
из планиметрии известно, что
![]() (см. рис. 16). Отсюда
(см. рис. 16). Отсюда
![]() .
.
Тогда
![]() .
.
Из этой формулы
получается условие параллельности двух
прямых:
![]() ;
и условие перпендикулярности двух
прямых:
;
и условие перпендикулярности двух
прямых:
![]()
![]() .
.
2. Кривые второго порядка в R2
Общее уравнение кривой второго порядка на плоскости имеет вид:
![]() .
.
Справедлива следующая теорема (дается без доказательства).
Теорема. Общее уравнение кривой второго порядка на плоскости с помощью поворота и параллельного переноса прямоугольной системы координат может быть приведено к одному из следующих канонических уравнений:
-
 - эллипс (рис. 17);
- эллипс (рис. 17); -
 - гипербола (рис.
18);
- гипербола (рис.
18); -
 - парабола (рис.
19);
- парабола (рис.
19); -
 -
пара пересекающихся прямых;
-
пара пересекающихся прямых; -
 -
пара параллельных прямых;
-
пара параллельных прямых; -
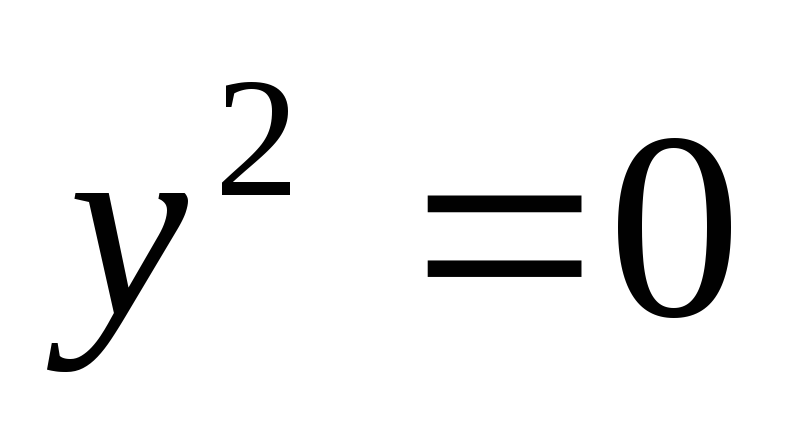 - прямая (пара
совпадающих прямых);
- прямая (пара
совпадающих прямых); -
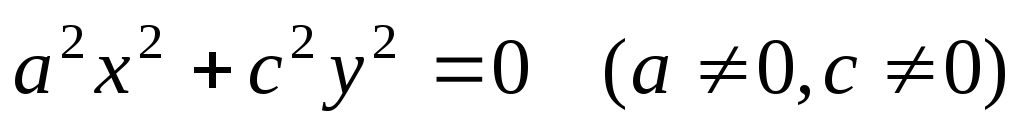 - точка (вырожденный
эллипс);
- точка (вырожденный
эллипс); -
 -
пустое множество (мнимый эллипс).
-
пустое множество (мнимый эллипс).
Приведем основные геометрические свойства кривых 1-3, которые выводятся из их канонических уравнений, т.е. решим задачу первого типа, заключающуюся в изучении свойств линии при помощи заранее данного уравнения этой линии (см. лекцию 5). Такое изучение проведем средствами математического анализа.
-
 .
Эллипс имеет две оси симметрии Ох
и Оу, называемые осями, центр симметрии
О, называемый центром. Точки пересечения
эллипса с осями называются его вершинами.
Эллипс имеет четыре вершины. В силу
симметрии эллипса разрешим его уравнение
относительно у и положим
.
Эллипс имеет две оси симметрии Ох
и Оу, называемые осями, центр симметрии
О, называемый центром. Точки пересечения
эллипса с осями называются его вершинами.
Эллипс имеет четыре вершины. В силу
симметрии эллипса разрешим его уравнение
относительно у и положим
 .
Получим функцию
.
Получим функцию
 ,
, исследуем ее
исследуем ее
о сновные
свойства и построим график. Функция –
четная, т.к. у(-х)=у(х).
сновные
свойства и построим график. Функция –
четная, т.к. у(-х)=у(х).
Найдем
![]() ;
;
![]()
Получим интервалы монотонности (-а;0), (0;а).
Исследуем знак
у(х) на каждом из
этих интервалов:
![]() .
.
Из достаточных условий монотонности следует, что функция у(х) возрастает на (-а,0) и убывает на (0,а). Точка х=0 – точка max функции.
Вторая производная
функции
![]() показывает, что график функции выпуклый
на (-а;а). (Дополнительные сведения
к исследованию функции).
показывает, что график функции выпуклый
на (-а;а). (Дополнительные сведения
к исследованию функции).
Согласно исследования построим эллипс (рис. 17).
На рис. 17 указаны
точки
![]() ,
где
,
где
![]() ,
называемые фокусами эллипса; ось
,
называемые фокусами эллипса; ось
![]() называется фокальной осью эллипса, а –
большая, b – малая
полуоси эллипса (при условии, что
a>b).
называется фокальной осью эллипса, а –
большая, b – малая
полуоси эллипса (при условии, что
a>b).
Эллипс есть
множество всех точек М плоскости, для
которых
![]() .
Форма эллипса (мера его сжатия)
характеризуется его эксцентриситетом
.
Форма эллипса (мера его сжатия)
характеризуется его эксцентриситетом![]() .
Так как c<a,
то
.
Так как c<a,
то
![]()
В частном случае,
когда
![]() ,
эллипс превращается в окружность с
уравнением
,
эллипс превращается в окружность с
уравнением
![]() .
.
2. ![]() .
Гипербола имеет две оси симметрии
Ох и Оу, называемые ее осями, и центр
симметрии О, называемый ее центром.
Точки пересечения гиперболы с осями
называются вершинами. Гипербола
имеет две вершины. Ось Ох пересекает
гиперболу и называется ее действительной
осью. Ось Оу не пересекает гиперболу
и называется ее мнимой осью.
.
Гипербола имеет две оси симметрии
Ох и Оу, называемые ее осями, и центр
симметрии О, называемый ее центром.
Точки пересечения гиперболы с осями
называются вершинами. Гипербола
имеет две вершины. Ось Ох пересекает
гиперболу и называется ее действительной
осью. Ось Оу не пересекает гиперболу
и называется ее мнимой осью.
В
Рис.
18 силу симметрии можно изучить свойства
той части гиперболы, которая расположена
в первой координатной четверти и
описывается уравнением
силу симметрии можно изучить свойства
той части гиперболы, которая расположена
в первой координатной четверти и
описывается уравнением
![]() .
.
Исследуя его,
как в предыдущем случае, т.е. с помощью
производных (сделать самостоятельно),
можно прийти к выводу, что функция
![]() ,
возрастает от 0 до +
,
возрастает от 0 до +![]() ,
причем график ее расположен ниже прямой
,
причем график ее расположен ниже прямой
![]() (рис.18).
(рис.18).
Гипербола
состоит из двух ветвей. Прямые с
уравнениями
![]() называются ее асимптотами. Точки
называются ее асимптотами. Точки
![]() ,
где
,
где
![]() ,
называются фокусами гиперболы, а
ось
,
называются фокусами гиперболы, а
ось
![]() - фокальной осью гиперболы. Гипербола
есть множество всех точек плоскости,
для которых
- фокальной осью гиперболы. Гипербола
есть множество всех точек плоскости,
для которых
![]() .
Форма гиперболы характеризуется ее
эксцентриситетом
.
Форма гиперболы характеризуется ее
эксцентриситетом
![]() .
Так как с>a, то
.
Так как с>a, то
![]() .
.
Если a=b, то гипербола называется равнобочной.
Две гиперболы
![]() называются сопряженными.
называются сопряженными.
3 .
. ![]() .
Парабола имеет ось симметрии Ох,
называемую ее осью. Точка пересечения
параболы с осью 0х– вершина
параболы. Точка
.
Парабола имеет ось симметрии Ох,
называемую ее осью. Точка пересечения
параболы с осью 0х– вершина
параболы. Точка
![]() на-зывается ее фокусом, а прямая с
уравнением
на-зывается ее фокусом, а прямая с
уравнением
![]() - директрисой параболы. Парабола
есть множество всех точек плоскости,
равноудаленных от фокуса и директрисы.
- директрисой параболы. Парабола
есть множество всех точек плоскости,
равноудаленных от фокуса и директрисы.
4. Приведение общего уравнения кривой второго прядка
![]() к каноническому виду.
к каноническому виду.
Одним из способов приведения общего уравнения второго порядка (в котором В=0) к каноническому виду является способ «выделения полных квадратов».
Например,
привести уравнение второго порядка
![]() к каноническому виду, установить тип
кривой и построить.
к каноническому виду, установить тип
кривой и построить.
Решение
![]()
Окончательно,
![]() - каноническое уравнение эллипса с осями
х=3 и у=-1, с центром О(3;-1), с полуосями
- каноническое уравнение эллипса с осями
х=3 и у=-1, с центром О(3;-1), с полуосями
![]() .
.
Выполним построение эллипса.