Математика ЗО от Белоусовой / Алгебра и геометрия и ТДУ / Лекции по АГиТДУ / Лекция 2

Лекция 2. Определители второго и третьего порядков

Понятие определителя (детерминанта) возникло при решении линейных систем, у которых число уравнений совпадает с числом неизвестных.

Пользуясь этим понятием, можно указать формулы, которые дают решения такой системы через ее коэффициенты и свободные члены.

Роль определителей в математике очень велика. При изучении линейной алгебры мы будем часто к ним обращаться.

Определители второго порядка

Р

(2.1)

ассмотрим систему двух линейных уравнений с двумя неизвестными

к

(2.2)

оэффициенты которой a_ijR. Составим квадратную таблицу, называемую матрицей второго порядка:

Умножая обе части первого уравнения на a₂₂, обе части второго уравнения на (-а₁₂), затем складывая, исключим неизвестное х₂:

(а₁₁а₂₂-а₁₂а₂₁) х₁=(b₁а₂₂ -а₁₂b₂).

Аналогично, получим

(а₁₁а₂₂-а₁₂а₂₁) х₂=(b₁а₁₁ –а₂₁b₁).

П

(2.3)

редположим, что а₁₁а₂₂-а₁₂а₂₁0. Тогда

.

При сделанном предположении формулы (2.3) служат единственным решением системы (2.1).

Выражения (2.3) имеют один и тот же знаменатель, который очень просто выражается через элементы матрицы (2.2): а₁₁а₂₂-а₁₂а₂₁.

Это число называется определителем матрицы (2.2) (определителем или детерминантом второго порядка) и обозначается следующим образом: .

Итак, согласно определению,

.

Пример:

Обладая понятием определителя второго порядка, формулы (2.3) можно переписать в следующем виде:

(2.4)

Определители третьего порядка

Перейдем теперь к системе трех уравнений с тремя неизвестными:

(2.5)

с матрицей

(2.6)

.

Если умножить обе части первого уравнения системы (2.5) на число а₂₂а₃₃-а₂₃а₃₂, обе части второго уравнения – на число а₁₃а₃₂-а₁₂а₃₃, обе части третьего уравнения – на число а₁₂а₂₃-а₁₃а₂₂ и сложить все три уравнения, то коэффициенты при неизвестных х₂ и х₃ окажутся равными нулю, и мы получим равенство

(2.7)

(а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₁+а₁₃а₂₁а₃₂-а₁₃а₂₂а₃₁-а₁₂а₂₁а₃₃-а₁₁а₂₃а₃₂)х₁= =(b₁а₂₂а₃₃+а₁₂а₂₃b₃+а₁₃b₂а₃₂-а₁₃а₂₂b₃-а₁₂b₂а₃₃-b₁а₂₃а₃₂).

Коэффициент при х₁ в этом равенстве выражается через элементы матрицы (2.6) и называется определителем этой матрицы (определителем или детерминантом третьего порядка). Для его записи применяется такая же символика, как и в случае определителей второго порядка. Итак,

(2.8)

.

Несмотря на то, что выражение (2.8) довольно сложное, все же закон, по которому оно составляется из элементов матрицы (2.6), довольно прост и указан схематично на рис.1

Рис.1

Слева на рис.1 дано правило вычисления положительных членов определителя, справа – правило вычисления его отрицательных членов.

Указанное правило вычисления определителя третьего порядка носит название правила Саррюса (или правила треугольников).

Пример

Обозначим определитель (2.8) символом , а определитель матрицы, полученной из матрицы (2.6) заменой ее j-го столбца (j=1,2,3) столбцом из свободных членов системы (2.5), - символом j. Тогда нетрудно проверить, что правая часть равенства (2.7) есть ₁, а само равенство (2.7) приобретает вид х₁=₁.

Предположим, что 0. Тогда х₁=₁ / . Аналогично, умножая уравнения системы (2.5) соответственно на числа а₁₃а₃₁-а₂₁а₃₃, а₁₃а₃₃-а₁₃а₃₁, а₁₃а₂₁-а₁₁а₂₃, получаем х₂=₂  х₂=₂ / .

Наконец, умножая эти уравнения соответственно на числа а₂₁а₃₂-а₂₂а₃₁, а₁₂а₃₁-а₁₁а₃₂, а₁₁а₂₂-а₁₂а₂₁, получаем х₃=₃  х₃=₃ / .

Итак, если 0, то система (2.5) имеет решение, которое определяется однозначно и имеет вид:

.

Если сравнить формулы решения линейных систем (2.1) и (2.3), то видно, что формулы решения системы (2.1) можно записать в том же самом виде, что и формулы решения системы (2.5). Эти формулы называются формулами Крамера, а указанное правило решения систем (2.1) и (2.5) носит название правила Крамера.

Свойства определителей второго и третьего порядков

Свойство 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, т.е.

.

Это свойство указывает на равноправие строк и столбцов.

Свойство 2. При перестановке двух каких-либо столбцов (строк) определитель изменит только знак.

Оба свойства проверяются непосредственно вычислением определителей, о которых идет речь.

Свойство 3. Определитель матрицы, имеющей два одинаковых столбца (строки), равен нулю.

Доказательство. Если одинаковые столбцы поменять местами, то с одной стороны, по свойству 2, определитель должен сменить знак, с другой стороны, величина определителя не изменится. Это возможно тогда и только тогда, когда число равно нулю.

Замечание. Свойство 3 можно проверить аналогично свойству 1 и 2.

Свойство 4. Если все элементы какого-либо столбца (сроки) определителя имеют общий множитель, то его можно вынести за знак определителя.

Например, .

Действительно,

.

Свойство 5. Если все элементы какого-либо столбца (строки) определителя – нули, то определитель равен нулю.

Свойство 6. Определитель, содержащий два пропорциональных столбца (строки), равен нулю.

Свойства 5-6 являются прямыми следствиями свойств 3-4.

Свойство 7. Если все элементы j-го столбца (строки) определителя представлены в виде сумы двух слагаемых а_ij = b_ij + c_ij, i=1,2,3, то определитель равен сумме двух определителей, у которых все столбцы (строки), кроме j-го, такие же , как и в заданном определителе, а j-й столбец в одном из слагаемых состоит из элементов b_ij, в другом – из с_ij .

Например,

.

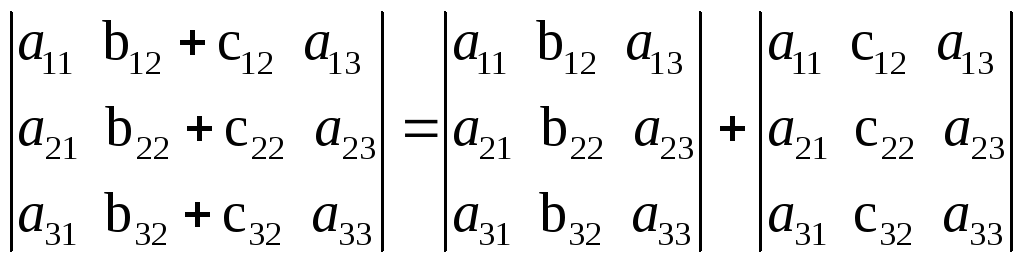Равенство проверить самостоятельно непосредственным вычислением определителей, стоящих в правой и левой его частях.

Свойство 8. Если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель, то величина определителя при этом не изменится.

Например, .

Проверить свойство самостоятельно.

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента а_ij определителя третьего порядка называется определитель второго порядка, получаемый из данного путем вычеркивания i-й строки и j-го столбца, на пересечении которых расположен этот элемент. Такой минор обозначается символом M_ij.

Например, для определителя (2.8) минором элемента а₁₁ является определитель , а минором элемента а₂₃ – определитель .

Надо заметить, что эти миноры не содержат элементы той строки и того столбца, на пересечении которых расположен указанный элемент.

Алгебраическое дополнение элемента а_ij определителя (2.8) равен минору этого элемента, умноженному на (-1)^i+j. Обозначается алгебраическое дополнение элемента А_ij символом А_ij. По определению, А_ij=(-1)^i+j M_ij.

Например, А₁₁ элемента а₁₁ равняется минору М₁₁, взятому со своим знаком, т.е.

,

а алгебраическое дополнение элемента а₂₃ равно минору М₂₃, взятому с противоположным знаком, т.е.

.

Свойство 9. (Теорема разложения). Определитель равен сумме произведений элементов какого-либо столбца (строки) на их алгебраические дополнения. Иначе говоря, имеют место следующие равенства:

(Формула разложения определителя по элементам j-го столбца).

(Формула разложения определителя по элементам i-й строки).

Пример

Применяя свойство 8, можно получить два нуля в каком-либо столбце или строке, тогда вычисление определителя становится проще.

Получим еще один ноль в первой строке определителя, прибавив к элементам второго столбца соответствующие элементы первого столбца, предварительно умноженные на число 2. Тогда

Свойство 10 (Теорема замещения). Сумма произведений произвольных трех чисел b₁, b₂, b₃ на алгебраические дополнения элементов какого-либо столбца (строки) матрицы (2.6) равна определителю матрицы, которая получается из данной заменой элементов указанного столбца (строки) на числа b₁, b₂, b₃ .

Например, .

Свойство 11 (Теорема аннулирования). Сумма произведений элементов одного столбца (строки) матрицы (2.6) на алгебраические дополнения элементов другого столбца (строки) равна нулю.

Например, .

Эти два свойства являются следствиями свойства 9.