
Математика ЗО от Белоусовой / Математический анализ, лекции 2 семестр / Лекция 12
.doc12. Лекционное занятие. ТЕОРИЯ СКАЛЯРНОГО И ВЕКТОРНОГО ПОЛЯ
12.1 Скалярное поле
Скалярное
поле – это область пространства,
в которой задана скалярная функция
![]() ,
называемая функцией поля. Например, это
может быть поле температур, поле давлений
и т.д.
,
называемая функцией поля. Например, это
может быть поле температур, поле давлений
и т.д.
Множество
точек поля, в которых функция поля
![]() принимает постоянное значение
принимает постоянное значение
![]() ,
образует поверхность с уравнением
,
образует поверхность с уравнением
![]() ,
называемую поверхностью уровня
поля. Если скалярное поле плоское,
например, находится в
плоскости
,
называемую поверхностью уровня
поля. Если скалярное поле плоское,
например, находится в
плоскости
![]() ,
то его функция поля
,
то его функция поля
![]() зависит от двух переменных
зависит от двух переменных
![]() и
и
![]() ,
а множество точек,
в которых
,
а множество точек,
в которых
![]() ,
образуют линию уровня. Линии
уровня используются при составлении
географических карт (для изображения
точек, расположенных на одинаковой
высоте над уровнем моря), при составлении
метеорологических карт (для изображения
линий одинаковых температур – изотерм
и линий одинакового давления – изобар).
,
образуют линию уровня. Линии
уровня используются при составлении
географических карт (для изображения
точек, расположенных на одинаковой
высоте над уровнем моря), при составлении
метеорологических карт (для изображения
линий одинаковых температур – изотерм
и линий одинакового давления – изобар).
12.2 Производная поля по направлению
Д ля
характеристики скорости изменения поля
ля
характеристики скорости изменения поля
![]() в направлении вектора
в направлении вектора
![]() введем понятие производной поля по
направлению. Пусть задана точка
введем понятие производной поля по
направлению. Пусть задана точка
![]() и вектор
и вектор
![]() ,
выходящий из точки
,
выходящий из точки
![]() (рис. 1). Рассмотрим точку
(рис. 1). Рассмотрим точку
![]() ,
лежащую на векторе
,
лежащую на векторе
![]() ,
и величину
,
и величину
![]() – приращение функции поля
– приращение функции поля
![]() в точке
в точке
![]() в направлении
в направлении
![]() .
.
Производной
поля
![]() в точке
в точке
![]() в направлении
в направлении
![]() называют величину
называют величину

12.3 Свойства производной по направлению
1).
Скорость изменения функции
![]() в точке
в точке
![]() в направлении
в направлении
![]() равна
равна
 .
.
2).
Поле
![]() в точке
в точке
![]() в направлении
в направлении
![]() возрастает тогда и только тогда, когда
возрастает тогда и только тогда, когда
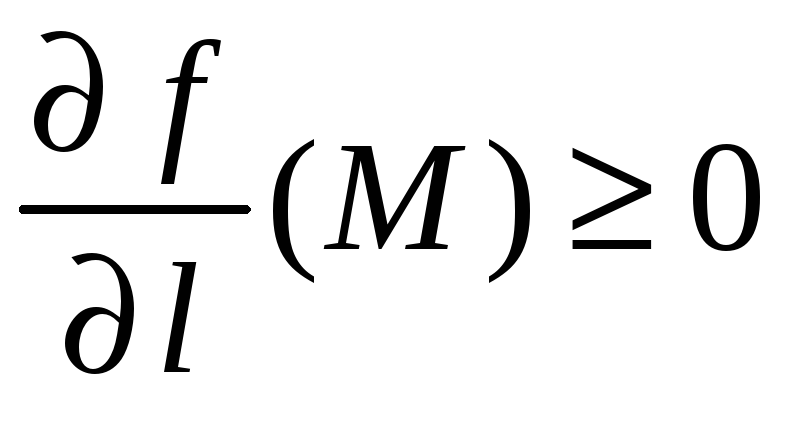 .
.
3).
Поле
![]() в точке
в точке
![]() в направлении
в направлении
![]() убывает тогда и только тогда, когда
убывает тогда и только тогда, когда
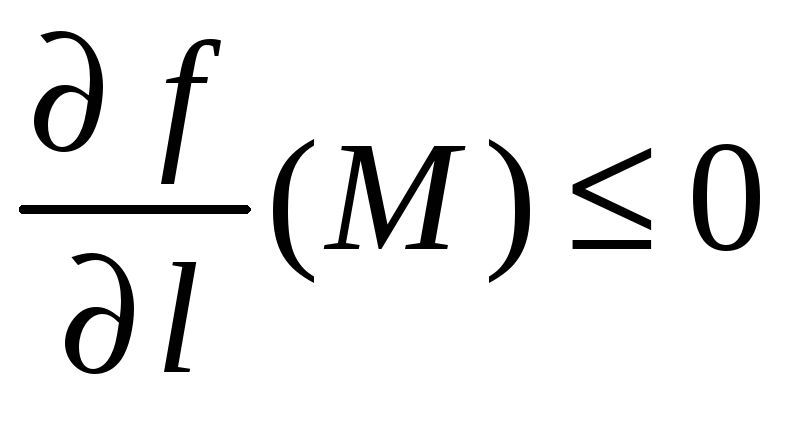 .
.
4).
Если
![]() ,
то
,
то
 ;
если
;
если
![]() ,
то
,
то
 .
.
Действительно,
1)
![]() есть изменение функции
есть изменение функции
![]() на участке
на участке
![]() ,
,
 есть средняя скорость изменения функции
есть средняя скорость изменения функции
![]() на участке
на участке
![]() ,
,
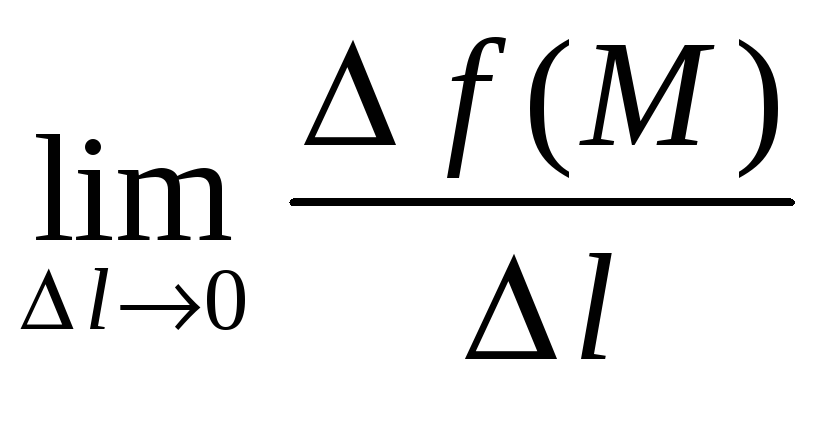 есть скорость изменения функции
есть скорость изменения функции
![]() в точке
в точке
![]() в направлении
в направлении
![]() ;
;
2) в
направлении
![]() поле
поле
![]() возрастает
возрастает
![]()
![]()

![]()
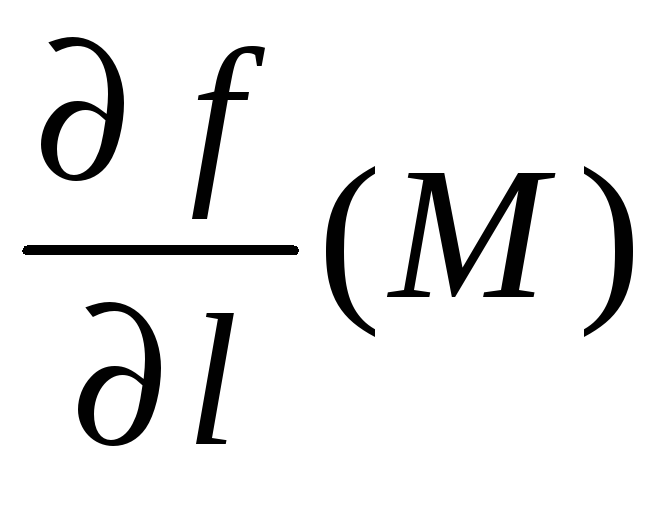
![]() ;
;
-
следующее свойство проверяется так же, как предыдущее свойство;
-
если, например,
 ,
то
,
то
 и потому
и потому
 .
.
12.4 Формула для вычисления производной по направлению
Пусть
функция
![]() – дифференцируема в точке
– дифференцируема в точке
![]() .
Тогда
.
Тогда
![]() ,
,
где
![]() и
и
 .
.
Поделим
равенство (8.1) на
![]() :
:
![]() .
.
Рассмотрим
вектор
![]() ,
называемый градиентом
поля
,
называемый градиентом
поля
![]() ,
и вектор
,
и вектор
 ,
равный единичному вектору направления
,
равный единичному вектору направления
![]() .
Тогда равенство (8.2) можно записать в
виде
.
Тогда равенство (8.2) можно записать в
виде
 ,
,
где
первое слагаемое есть скалярное
произведение векторов
![]() и
и
![]() .
.
В
пределе при
![]() ,
стремящемся к нулю, получим:
,
стремящемся к нулю, получим:
 ,
,
где
![]() ─
градиент скалярного поля
─
градиент скалярного поля
![]() ,
,
 ─ единичный вектор направления
─ единичный вектор направления
![]() .
.
12.5 Градиент поля и его свойства
Вектор
![]() является важной характеристикой
скалярного поля. Введем условный оператор
является важной характеристикой
скалярного поля. Введем условный оператор
 (оператор Гамильтона или вектор “набла”).
С его помощью удобно записать градиент
скалярного поля
(оператор Гамильтона или вектор “набла”).
С его помощью удобно записать градиент
скалярного поля
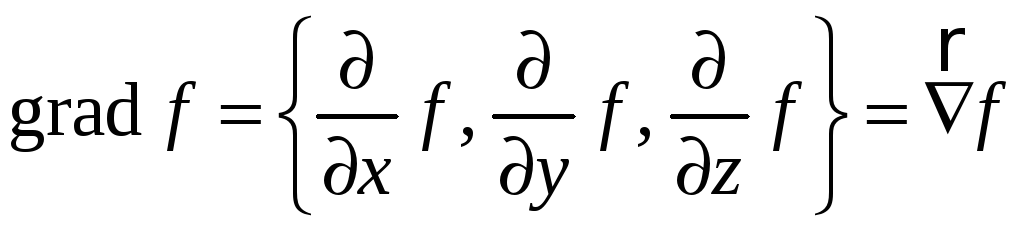 .
.
Отметим ряд свойств градиента.
1).
Скалярное поле
![]() в точке
в точке
![]() быстрее всего возрастает в направлении
вектора
быстрее всего возрастает в направлении
вектора
![]() со скоростью, равной
со скоростью, равной
![]() .
.
2).
Скалярное поле
![]() в точке
в точке
![]() быстрее всего убывает в направлении,
противоположном вектору
быстрее всего убывает в направлении,
противоположном вектору
![]() ,
со скоростью, равной
,
со скоростью, равной
![]() .
.
3).
Вектор
![]() направлен по нормали к поверхности
уровня поля
направлен по нормали к поверхности
уровня поля
![]() ,
проходящей через точку
,
проходящей через точку
![]() .
.
4). Дифференциальные свойства:

Проверим эти свойства.
1. Из формулы и определения скалярного произведения следует, что
 ,
,
где
![]() ─ угол между векторами
─ угол между векторами
![]() и
и
![]() .
Так как длина единичного вектора
.
Так как длина единичного вектора
![]() равна единице, то
равна единице, то
 .
.
Поэтому
 принимает наибольшее значение, равное
принимает наибольшее значение, равное
![]() ,
когда
,
когда
![]() =1,
то есть угол
=1,
то есть угол
![]() между векторами
между векторами
![]() и
и
![]() равен
нулю и
равен
нулю и
![]()
![]()
![]() .
.
2.
Производная
 будет принимать наименьшее значение,
когда
будет принимать наименьшее значение,
когда
![]() ,
т.е. угол
,
т.е. угол
![]() =
=![]() и
и
![]()
![]()
![]() .
.
3.
Поверхность уровня поля
![]() имеет уравнение
имеет уравнение
![]() .
Нормальный вектор этой поверхности
.
Нормальный вектор этой поверхности
![]() совпадает с
совпадает с
![]() .
Значит, вектор
.
Значит, вектор
![]() направлен по нормали к поверхности
уровня поля
направлен по нормали к поверхности
уровня поля
![]() ,
проведенной в точке
,
проведенной в точке
![]() .
.
4.1.
![]()
аналогично проверяются свойства 4.2), 4.3), 4.4);
для
проверки свойства 4.5) учтем, что
![]()
![]()
 аналогично,
аналогично,
![]() и поэтому
и поэтому
 .
.
Из первого и третьего свойств следует инвариантное определение градиента, т.е. определение, не зависящее от системы координат:
Градиент
скалярного поля
![]() в точке
в точке
![]() есть вектор, который
есть вектор, который
а)
по величине равен наибольшей скорости
возрастания поля
![]() в точке
в точке
![]() ,
,
б)
направлен по нормали к поверхности
уровня поля
![]() ,
проходящей через точку
,
проходящей через точку
![]() ,
в сторону наибольшего возрастания поля.
,
в сторону наибольшего возрастания поля.
Пример
1. Найти
наибольшую скорость возрастания поля
![]() в точке
в точке
![]() .
.
Решение. Найдем градиент поля:
![]() .
.
Наибольшая
скорость возрастания поля в точке
![]() равна
равна
![]()
Пример 2. Доказать оптическое свойство эллипса: лучи, выходящие из одного фокуса эллипса, после отражения от эллипса проходят через другой фокус эллипса.
Решение.
Пусть
![]() фокусы
эллипса;
фокусы
эллипса;
![]() . Рассмотрим
. Рассмотрим
с калярное
поле
калярное
поле
![]() .
По определению эллипса точка
.
По определению эллипса точка
![]() принадлежит эллипсу тогда и только
тогда, когда
принадлежит эллипсу тогда и только
тогда, когда
![]() ,
т.е. эллипс есть линия уровня скалярного
поля
,
т.е. эллипс есть линия уровня скалярного
поля
![]() ;
поэтому
;
поэтому
 направлен по нормали к эллипсу в точке
направлен по нормали к эллипсу в точке
![]() .
Кроме того, этот вектор направлен по
диагонали параллелограмма, построенного
на векторах
.
Кроме того, этот вектор направлен по
диагонали параллелограмма, построенного
на векторах
 .
Длины этих векторов равны единице,
поэтому параллелограмм является ромбом
и его диагональ является биссектрисой
угла ромба, т.е.
.
Длины этих векторов равны единице,
поэтому параллелограмм является ромбом
и его диагональ является биссектрисой
угла ромба, т.е.
![]() .
Тогда
.
Тогда
![]() ,
как углы дополнительные до
прямого. Так как
,
как углы дополнительные до
прямого. Так как
![]() то
то
![]() т.е. луч, выходящий из фокуса
т.е. луч, выходящий из фокуса
![]() эллипса, после отражения от эллипса
пройдет через другой фокус
эллипса, после отражения от эллипса
пройдет через другой фокус
![]() .
.
12.6 Векторное поле и векторные линии
Векторное
поле – это область пространства, в
каждой точке
![]() которой задан вектор
которой задан вектор
![]() .
.
Пример
1. Пусть на материальную точку в
области
![]() действует сила
действует сила
![]() .
Тогда в области
.
Тогда в области
![]() определено векторное поле
определено векторное поле
![]() .
.
Пример
2. Пусть в области
![]() происходит течение жидкости и в каждой
точке
происходит течение жидкости и в каждой
точке
![]() задан вектор
задан вектор
![]() скорости частицы жидкости. Тогда в
области
скорости частицы жидкости. Тогда в
области
![]() определено векторное поле скоростей
жидкости.
определено векторное поле скоростей
жидкости.
Пример
3. Поместим заряд
![]() в начало координат. Тогда сила, с которой
этот заряд действует на единичный
положительный заряд, помещенный в точку
в начало координат. Тогда сила, с которой
этот заряд действует на единичный
положительный заряд, помещенный в точку
![]() ,
определяется по закону Кулона:
,
определяется по закону Кулона:
![]() ,
,
где
![]() ─ вектор, идущий из начала координат в
точку
─ вектор, идущий из начала координат в
точку
![]() (радиус-вектор точки
(радиус-вектор точки
![]() ),
),
![]() ─
его длина. Имеем векторное поле
напряженностей
─
его длина. Имеем векторное поле
напряженностей
![]() ,
создаваемое зарядом
,
создаваемое зарядом
![]() .
.
Мы
будем рассматривать только стационарные
поля, для которых вектор поля
![]() зависит от точки
зависит от точки
![]() и не зависит от времени. Проекции вектора
и не зависит от времени. Проекции вектора
![]() на оси координат обозначим
на оси координат обозначим
![]() .
Тогда:
.
Тогда:
![]() .
.
Далее
всюду предполагаем, что функции
![]() непрерывны вместе со своими частными
производными; в противном случае точку
поля назовем особой.
непрерывны вместе со своими частными
производными; в противном случае точку
поля назовем особой.
Одной из характеристик векторного поля являются векторные линии.
Векторной линией векторного поля называют линию, в каждой точке которой касательный вектор коллинеарен вектору поля (рис. 3).
Векторные линии в конкретных полях имеют ясный физический смысл.
В поле скоростей текущей жидкости векторные
линии – это линии тока этой жидкости,
т. е. линии, по которым движутся частицы
жидкости.
поле скоростей текущей жидкости векторные
линии – это линии тока этой жидкости,
т. е. линии, по которым движутся частицы
жидкости.
В электрическом поле векторные линии – это силовые линии и их расположение очень важно в физике.
Выведем
уравнения векторных линий для поля
![]() (для краткости аргументы функций
(для краткости аргументы функций
![]() не выписаны).
не выписаны).
Пусть
уравнения векторной линии
![]() ,
(
,
(![]() параметр).
Касательным вектором этой линии является
вектор
параметр).
Касательным вектором этой линии является
вектор
![]() и вектор
и вектор
![]() .
.
По
определению векторной линии ее касательный
вектор
![]() и вектор поля
и вектор поля
![]() коллинеарны.
Поэтому координаты этих векторов
пропорциональны, т. е.
коллинеарны.
Поэтому координаты этих векторов
пропорциональны, т. е.
 .
.
Пример
4. Магнитное
поле
![]() создано электрическим током силы
создано электрическим током силы
![]() ,
текущим по бесконечно длинному прямому
проводу
,
текущим по бесконечно длинному прямому
проводу
![]() .
Найти силовые линии этого поля.
.
Найти силовые линии этого поля.
Решение.
Если провод
![]() принять за ось
принять за ось
![]() некоторой декартовой системы координат,
то, как известно из физики,
некоторой декартовой системы координат,
то, как известно из физики,
 .
.
Запишем
уравнения векторных линий для поля
![]() :
:
 или
или
 .
.
Из
первого уравнения имеем
![]() .
Из второго уравнения
.
Из второго уравнения
![]() .
Таким образом, силовые линии поля
.
Таким образом, силовые линии поля
![]() есть окружности
есть окружности
![]() ,
расположенные в плоскостях
,
расположенные в плоскостях
![]() ,
параллельных плоскости
,
параллельных плоскости
![]() .
.
Пример
5. Найти векторные линии поля
![]() .
.
Решение.
Учитывая, что
![]() ,
запишем систему:
,
запишем систему:
 .
.
В одном
из уравнений этой системы
![]() разделим переменные:
разделим переменные:
![]() .
.
Теперь
проинтегрируем
![]() и получим
и получим
![]() или
или
![]() .
.
Чтобы
решить другое уравнение системы,
воспользуемся известным свойством
пропорций: если
![]() ,
то
,
то
 .
В нашем примере удобно взять
.
В нашем примере удобно взять
![]() ,
,
![]() и записать систему уравнений следующим
образом:
и записать систему уравнений следующим
образом:
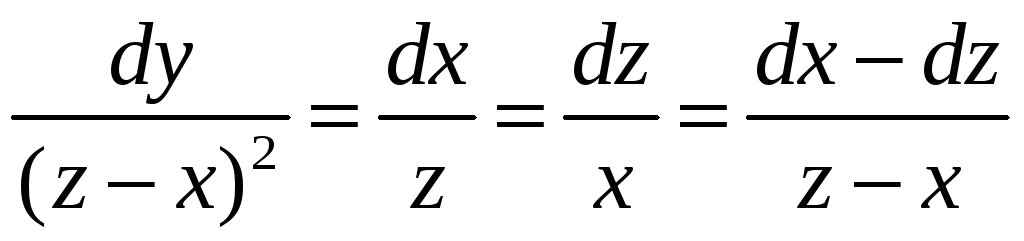 или
или
 .
.
Разделим
переменные:
![]() .
Проинтегрируем
.
Проинтегрируем
![]() и получим
и получим
![]() .
Таким образом, векторные линии данного
поля есть линии пересечения поверхностей
.
Таким образом, векторные линии данного
поля есть линии пересечения поверхностей
![]() и
и
![]() .
.
Оглавление
12. Лекционное занятие. ТЕОРИЯ СКАЛЯРНОГО И ВЕКТОРНОГО ПОЛЯ 1
12.1 Скалярное поле 1
12.2 Производная поля по направлению 1
12.3 Свойства производной по направлению 2
12.4 Формула для вычисления производной по направлению 3
12.5 Градиент поля и его свойства 4
12.6 Векторное поле и векторные линии 7
Оглавление 11
