
Математика ЗО от Белоусовой / Математический анализ, лекции 2 семестр / Лекция 11
.doc11. Лекционное занятие. ТРОЙНОЙ ИНТЕГРАЛ В СФЕРИЧЕСКИХ КООРДИНАТАХ.
П оложение
точки
оложение
точки
![]() в пространстве можно охарактеризовать
с помощью сферических координат
в пространстве можно охарактеризовать
с помощью сферических координат
![]() ,
где
,
где
![]() длина
радиус-вектора точки
длина
радиус-вектора точки
![]() (рис. 1,
(рис. 1,
![]() угол
отклонения радиус-вектора точки
угол
отклонения радиус-вектора точки
![]() от оси
от оси
![]() ,
,
![]() угол
отклонения проекции на плоскость
угол
отклонения проекции на плоскость
![]() радиус-вектора точки
радиус-вектора точки
![]() от оси
от оси
![]()
Установим связь между прямоугольными
и сферическими координатами. Из
прямоугольного треугольника
![]() имеем
имеем
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]()
Вычислим якобиан
 .
.
Раскроем определитель по элементам третьей строки
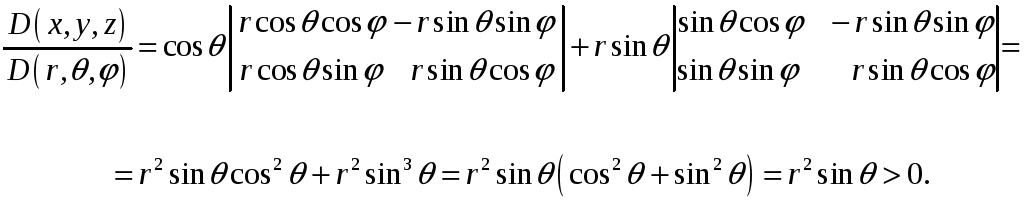
Тогда элемент объема в сферических координатах
![]()
Для вычисления тройного интеграла![]() следует
следует
1) заменить
![]() на их выражения в сферической системе
координат,
на их выражения в сферической системе
координат,
![]()
2) заменить область
![]() изменения переменных
изменения переменных
![]() на область
на область
![]() изменения переменных
изменения переменных
![]() .
.
Замечания
1). К сферическим координатам целесообразно
переходить, когда тело ограничено сферой
![]() ,
конусом
,
конусом
![]() или поверхностью, уравнение которой
содержит
или поверхностью, уравнение которой
содержит
![]() .
.
2). Наиболее удобен порядок интегрирования
(слева направо) по
![]()
3). Сначала расставить пределы интегрирования
по
![]() (двигаясь по лучу из начала координат),
потом ─ по
(двигаясь по лучу из начала координат),
потом ─ по
![]() (двигаясь от оси
(двигаясь от оси
![]() ),
потом ─ по
),
потом ─ по
![]() .
.
4). Если уравнение границы области или
подынтегральная функция содержат
 ,
то следует перейти к обобщенным
сферическим координатам
,
то следует перейти к обобщенным
сферическим координатам
![]() тогда
тогда
 ,
,
![]()
Пример 1. Вычислить момент инерции
относительно плоскости
![]() однородного (с плотностью
однородного (с плотностью
![]() )
тела, ограниченного поверхностями
)
тела, ограниченного поверхностями
![]()
![]()
Решение. Момент инерции тела вычислим по формуле
![]()

Так как тело ограничено сферой и
конусом (рис. 2), то перейдем к сферическим
координатам. При этом, учитывая формулы
(7.30), уравнение сферы примет вид
![]() или
или
![]() ;
уравнение конуса примет вид
;
уравнение конуса примет вид
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
.
Используя формулы, получим

П ример
2. Найти объем тела, ограниченного
поверхностью
ример
2. Найти объем тела, ограниченного
поверхностью
 .
.
Решение. Перейдем к обобщенным сферическим координатам
![]() .
В этих координатах
.
В этих координатах

и уравнение поверхности примет вид
![]() или
или
![]() .
.
По условию
![]() ,
поэтому
,
поэтому
![]() и
и
![]() .
Cоставим
таблицу:
.
Cоставим
таблицу:
Построим точки с
вычисленными координатами
![]() сначала при
сначала при
![]() ,
т.е. в
,
т.е. в
плоскости
![]() (рис. 3). Так как уравнение поверхности
(рис. 3). Так как уравнение поверхности
![]() от
от
![]() не зависит, то при любом
не зависит, то при любом
![]() получим такую же линию; все эти линии
образуют поверхность вращения (рис. 3).
Объем тела, ограниченного этой
поверхностью, вычислим с учетом
соотношения при
получим такую же линию; все эти линии
образуют поверхность вращения (рис. 3).
Объем тела, ограниченного этой
поверхностью, вычислим с учетом
соотношения при
![]() :
:
![]()
Чтобы расставить
пределы изменения
![]() ,
будем двигаться в области
,
будем двигаться в области
![]() по лучам, выходящим из начала координат.
На каждом таком луче
по лучам, выходящим из начала координат.
На каждом таком луче
![]() меняется от значения
меняется от значения
![]() в начале координат до значения
в начале координат до значения
![]() на поверхности, ограничивающей область
на поверхности, ограничивающей область
![]() .
Кроме того, эта область заключена между
лучами
.
Кроме того, эта область заключена между
лучами
![]() и
и
![]() ,
,
![]() .
Поэтому
.
Поэтому
 .
.
11.1 Поверхностный интеграл первого рода
Вычисление поверхностного интеграла
1 рода
![]() сводится к вычислению двойного интеграла.
Рассмотрим несколько случаев.
сводится к вычислению двойного интеграла.
Рассмотрим несколько случаев.
Случай 1.
Пусть гладкая поверхность
![]() задана параметрическими уравнениями
задана параметрическими уравнениями
![]() или
или
![]() .
.
По определению,
поверхностный интеграл функции
![]() по поверхности
по поверхности
![]() есть предел интегральной суммы функции
есть предел интегральной суммы функции
![]() ,
который не зависит от способа разбиения
поверхности
,
который не зависит от способа разбиения
поверхности
![]() на ячейки:
на ячейки:

У добно
разбить поверхность
добно
разбить поверхность
![]() на ячейки
координатными
линиями
на ячейки
координатными
линиями
![]() Выделим одну из таких ячеек (рис. 4).
Рассмотрим радиус-векторы точек
Выделим одну из таких ячеек (рис. 4).
Рассмотрим радиус-векторы точек
![]() :
:
![]() Тогда
Тогда
![]()
![]()
и площадь ячейки
![]()
По аналогии с этим элемент площади поверхности
![]() .
.
Можно показать (строгое доказательство опускаем), что

Итак, получили следующее правило:
Для вычисления
поверхностного интеграла
![]() следует
следует
1) в подынтегральной функции подставить
вместо
![]() их значения на поверхности
их значения на поверхности
![]() ,
т.е.
,
т.е.
![]() ,
,
2) заменить элемент площади
![]() на выражение
на выражение
![]() ;
;
3) вычислить получившийся двойной
интеграл по области
![]() изменения переменных
изменения переменных
![]() .
.
Случай 2. Пусть гладкая поверхность
![]() задана уравнением, разрешенным
относительно
задана уравнением, разрешенным
относительно
![]() :
:
![]() .
Присоединив два очевидных тождества,
получим параметрические
уравнения поверхности
.
Присоединив два очевидных тождества,
получим параметрические
уравнения поверхности
![]()
 (
(![]() параметры);
тогда
параметры);
тогда
 ,
,
и по формуле (7.34) получим
![]() .
.
Итак, для вычисления
поверхностного интеграла
![]() следует:
следует:
1) в подынтегральной
функции заменить
![]() его значением
его значением
![]() на поверхности
на поверхности
![]() ,
,
2) заменить элемент площади
![]() на выражение
на выражение
![]() ,
,
3) вычислить
получившийся двойной интеграл по
проекции
![]() поверхности
поверхности
![]() на плоскость
на плоскость
![]() .
.
Случай 3. Пусть гладкая поверхность
![]() задана уравнением, разрешенным
относительно
задана уравнением, разрешенным
относительно
![]() :
:
![]() .
Тогда
.
Тогда

Здесь
![]() есть проекция поверхности
есть проекция поверхности
![]() на плоскость
на плоскость
![]() .
.
Случай 4. Пусть гладкая поверхность
![]() задана уравнением, разрешенным
относительно
задана уравнением, разрешенным
относительно
![]() :
:
![]() .
Тогда
.
Тогда

Здесь
![]() есть проекция поверхности
есть проекция поверхности
![]() на плоскость
на плоскость
![]() .
.
Пример 1.
Найти массу однородной поверхности
![]() ,
,
![]() ,
если
,
если
![]() .
.
Рис. 5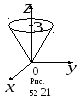



![]() методом сечений. В сечении
методом сечений. В сечении
![]() получаем
получаем
![]() или
или
![]() .
Это – пара прямых в плоскости
.
Это – пара прямых в плоскости
![]() (рис. 5). В сечении
(рис. 5). В сечении
![]() получаем окружность
получаем окружность
![]() .
Таким образом, уравнение
.
Таким образом, уравнение
![]() определяет коническую поверхность.
Массу поверхности найдем с помощью
поверхностного интеграла:
определяет коническую поверхность.
Массу поверхности найдем с помощью
поверхностного интеграла:
![]() .
.
Для вычисления
этого интеграла уравнение поверхности
удобно разрешить относительно
![]() :
:
![]() .
Найдем
.
Найдем
![]() ,
,
![]() и затем
и затем
![]() по первой из формул:
по первой из формул:

 .
.
Теперь вычислим
![]() ,
подставляя значение
,
подставляя значение
![]() на поверхности
на поверхности
![]() и
и
значение
![]() :
:
 .
.
Здесь
![]() есть проекция конической поверхности
есть проекция конической поверхности
![]() на плоскость
на плоскость
![]() ,
т.е. круг радиусом
,
т.е. круг радиусом
![]() (рис. 5). Двойной интеграл по кругу удобнее
вычислять в полярной системе координат.
Для этого заменим
(рис. 5). Двойной интеграл по кругу удобнее
вычислять в полярной системе координат.
Для этого заменим
![]() на
на
![]() ,
а
,
а
![]() на
на
![]() .
Получим
.
Получим
 .
.
Пример 2. Найти момент инерции
относительно начала координат полусферы
![]() ,
,
![]() ,
если плотность
,
если плотность
![]() .
.
Решение. Момент инерции относительно начала координат поверхности найдем с помощью поверхностного интеграла по второй из формул (6.13) :
![]() .
.
На поверхности сферы
![]() ,
,
![]() .
Поэтому
.
Поэтому
![]() .
.
Для вычисления этого интеграла разрешим
уравнение поверхности относительно
![]() ,
найдем
,
найдем
![]() ,
,
![]() и затем
и затем
![]() по первой из формул:
по первой из формул:
 ;
;
 .
.
Подставляя выражение для
![]() в интеграл, получим
в интеграл, получим
 .
.
Проекция
![]() полусферы на плоскость
полусферы на плоскость
![]() есть круг радиусом
есть круг радиусом
![]() ;
;
 равен площади
равен площади
![]() этого круга. Поэтому
этого круга. Поэтому
 .
.
Оглавление
11. Лекционное занятие. ТРОЙНОЙ ИНТЕГРАЛ В СФЕРИЧЕСКИХ КООРДИНАТАХ. 1
11.1 Поверхностный интеграл первого рода 4
Оглавление 9
