16. Лекционное занятие. ПОТЕНЦИАЛЬНОЕ ПОЛЕ.

Как и раньше, предполагаем, что координаты вектора поля ─ функции , , непрерывны и имеют частные производные.

Векторное поле называется потенциальным, если оно является полем градиента некоторой скалярной функции , т.е. ; при этом функцию называют скалярным потенциалом векторного поля.

Напомним, что . Так как , то 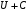также является потенциалом.

Свойства потенциального поля

1). Поле является потенциальным с потенциалом тогда и только тогда, когда .

2). Односвязное поле потенциально тогда и только тогда, когда в каждой точке поля .

3). В потенциальном поле линейный интеграл не зависит от формы пути.

4). В потенциальном поле циркуляция по любому контуру, не охватывающему особых точек поля, равна нулю.

5). В потенциальном поле циркуляции по контурам, охватывающим все особые точки поля, равны между собой.

6). В потенциальном поле линейный интеграл по дуге равен разности потенциалов конца и начала дуги.

Пусть ─ контуры, окружающие все особые точки поля; ориентируем контуры так, чтобы при обходе ограниченная ими область оставалась слева, т.е. против часовой стрелки, 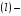по часовой стрелке; контуры с такой ориентацией обозначим соответственно . На поверхности с границей поле потенциально, и потому 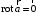по свойству 3) и теореме. Тогда по формуле Стокса

.

С другой стороны,

,

и, следовательно, .

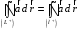6). Если поле 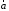потенциально и 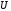─ его потенциал, то и по формуле

.

В силовом потенциальном поле свойства 3 и 6 означают, что работа сил поля по дуге не зависит от формы дуги и равна разности потенциалов конца и начала дуги.

Рассмотрим способы отыскания потенциала поля .

Отыскание потенциала по выражению

Воспользуемся первым свойством потенциального поля. Если удается представить выражение 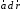в виде полного дифференциала некоторой функции , то поле ─ потенциально, а ─ его потенциал.

Пример 1. Показать, что поле потенциально и найти его потенциал, если

.

Решение

1). .

Следовательно, поле ─ потенциально; ─ его потенциал.

2). .

Следовательно, поле потенциально; ─ его потенциал.

3). .

Следовательно, поле ─ потенциально; 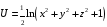─ его потенциал.

Отыскание потенциала по определению

Для потенциального поля и его потенциала имеем или в координатной форме

Проинтегрируем первое из этих равенств по ; при этом появится константа, не зависящая от переменной интегрирования (но зависящая от ):

.

Для отыскания функции следует подставить получившуюся функцию во второе и третье равенства.

Пример 2. Проверить, что поле является потенциальным и найти его потенциал.

Решение. Для данного поля проверить его потенциальность и найти потенциал по выражению сложно. Поэтому потенциальность поля проверим по условию , а потенциал найдем исходя из формул. Итак, вычислим ротор:

.

Значит поле потенциально и его потенциал 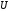удовлетворяет условию или в координатной форме

Проинтегрируем первое из этих равенств по

и подставим получившуюся функцию во второе и третье равенства:

Отсюда Следовательно, , где ─ константа. Поэтому

Отыскание потенциала центрального поля

Воспользуемся соотношением где . Тогда 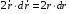и, значит, . Поэтому

.

Введем функцию . Так как , то . Следовательно, по свойству 1

центральное поле потенциально и его потенциал .

Пример 3. Найти потенциал поля напряженностей .

Решение. Поле ─ центральное, следовательно, оно потенциальное, и его потенциал .

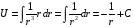Оглавление

16. Лекционное занятие. ПОТЕНЦИАЛЬНОЕ ПОЛЕ. 1

Свойства потенциального поля 1

Отыскание потенциала по выражению 3

Отыскание потенциала по определению 4

Отыскание потенциала центрального поля 6