10. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ТРОЙНОЙ ИНТЕГРАЛ, ЕГО ОСНОВНЫЕ СВОЙСТВА.

10.1. Тройной интеграл в прямоугольной системе

Вычисление тройного интеграла сводится к вычислению определенного и двойного интегралов. Рассмотрим три случая.

Случай 1. Пусть тело ограничено поверхностями , , цилиндрической поверхностью с образующими, параллельными оси (рис. 1,a). Цилиндрическая поверхность может и отсутствовать (рис. 1,б). Тогда

Здесь – есть проекция тела на плоскость (рис. 1).

Обоснование формулы проводится так же, как и для двойного интеграла.

0

х

х

Чтобы применять формулу на практике, рекомендуем:

1) построить тело ;

2) записать тройной интеграл через повторный интеграл; в повторном интеграле сначала расставить внутренние пределы интегрирования, т.е. пределы изменения . При этом переменная интегрирования меняется от на нижней поверхности до на верхней поверхности;

3) вычислить внутренний интеграл при фиксированных ;

4) вычислить внешний интеграл по проекции тела на плоскость .

Случай 2. Пусть тело ограничено поверхностями , и цилиндрической поверхностью с образующими, параллельными оси . Тогда

Случай 3. Пусть тело ограничено поверхностями , и цилиндрической поверхностью с образующими, параллельными оси . Тогда

Для вычисления тройных интегралов надо уметь строить поверхности с заданными уравнениями. Дадим следующие рекомендации.

1. Если уравнение поверхности не содержит одной переменной, например, уравнение не содержит , то поверхность является цилиндрической с образующими, параллельными оси . Сначала строим направляющую с заданным уравнением , затем через её точки проводим образующие, параллельные оси .

2. Если уравнение поверхности содержит переменные , то удобно строить поверхность методом сечения плоскостями , , или параллельными им плоскостями.

Пример 1. Найти объём тела, ограниченного поверхностями , , , .

Решение. Построим поверхности, ограничивающие тело. В уравнении отсутствует , следовательно, это уравнение определяет цилиндрическую поверхность с образующими, параллельными оси . Направляющая в плоскости имеет уравнение (или , ), которое определяет левую часть параболы. Строя направляющую и образующие, проходящие через её точки (рис. 2), получим цилиндрическую поверхность . Уравнение определяет плоскость .

Следующее уравнение есть уравнение первой степени, значит, оно определяет плоскость. В уравнении отсутствует , значит, плоскость параллельна оси . Кроме того, при имеем , при имеем . Через полученные две точки и проводим плоскость , параллельную оси . Эта плоскость пересечет плоскость по отрезку , а цилиндрическую поверхность – по дуге (рис. 2).

Аналогично, уравнение определяет плоскость, параллельную оси , пересекающую плоскость по отрезку , а цилиндрическую поверхность – по дуге .

Объём тела, ограниченного рассмотренными поверхностями, найдем по одной из формул (6.6):

.

Запишем тройной интеграл через повторный по формуле. Чтобы расставить внутренние пределы интегрирования, т.е. пределы изменения , будем двигаться параллельно оси . При этом меняется от на плоскости до на плоскости . Поэтому

.

Здесь есть проекция тела на плоскость , т.е. криволинейный треугольник . Вычислим теперь двойной интеграл. Для этого запишем его через повторный интеграл с внутренним интегрированием по . Для выяснения пределов изменения будем двигаться в области параллельно оси . При этом меняется от на дуге до на отрезке . Поэтому

.

Вычисляя сначала внутренний интеграл при фиксированном , а затем внешний интеграл, получим

.

Пример 2. Найти центр тяжести тела, ограниченного поверхностями , .

Решение. Построим поверхности, ограничивающие тело. Первую поверхность с уравнением построим методом сечений. В сечении плоскостью получим параболу с осью симметрии – осью (рис. 2). В сечении плоскостью получим окружность . По этим сечениям видно, что уравнение определяет параболоид. Вторая поверхность – плоскость – отсекает от параболоида его часть, изображенную на рис. 2.

Центр тяжести полученного однородного тела, в силу его симметрии, находится на оси (в точке ). Следовательно, . Координату центра тяжести тела найдем с помощью тройных интегралов по формулам:

, где .

Так как тело однородное, то его плотность является постоянной величиной и её можно вынести за знак интеграла. Поэтому

.

Вычислим сначала интеграл , стоящий в числителе; для этого запишем его в виде повторного интеграла с внутренним интегрированием по . Для выяснения пределов изменения будем двигаться параллельно оси . При этом меняется от на поверхности параболоида до на плоскости. Поэтому

Сначала вычислим внутренний интеграл

.

Так как проекция тела на плоскости есть круг, то получившийся двойной интеграл удобно вычислять в полярной системе координат, заменяя на , а на . Тогда получим

.

Двойной интеграл запишем через повторный с внутренним интегрированием по .

Так как сечение параболоида плоскостью есть окружность радиуса , то меняется от до ; меняется от до и, следовательно,

.

Аналогично вычисляется интеграл :

.

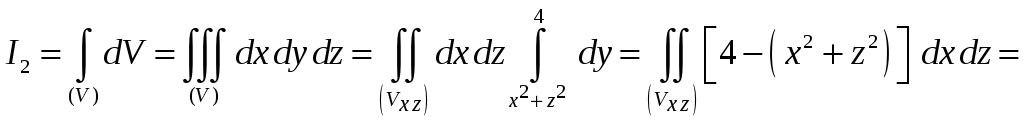
Итак, 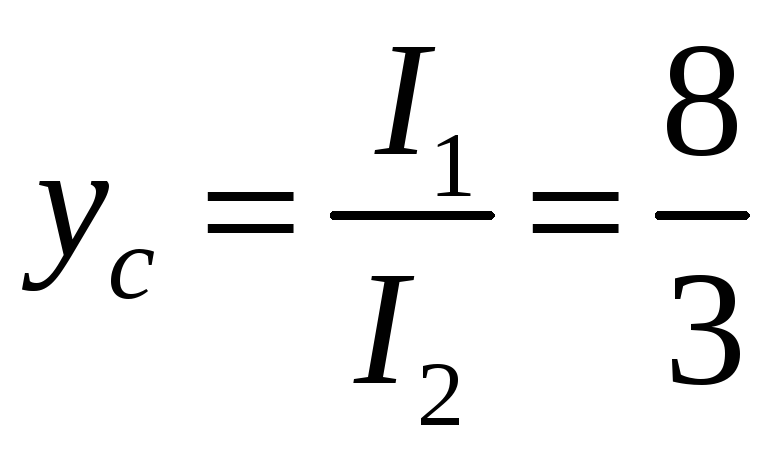и центр тяжести данного тела находится в точке .

10.2 Тройной интеграл в криволинейной системе

Для вычисления тройного интеграла иногда удобно использовать не прямоугольные координаты , а некоторые криволинейные координаты . Пусть известна связь между этими координатами

и .

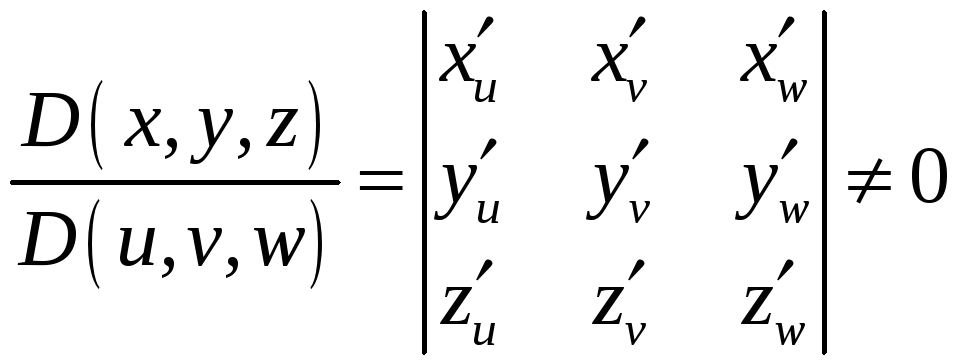Аналогично случаю двойного интеграла можно показать, что

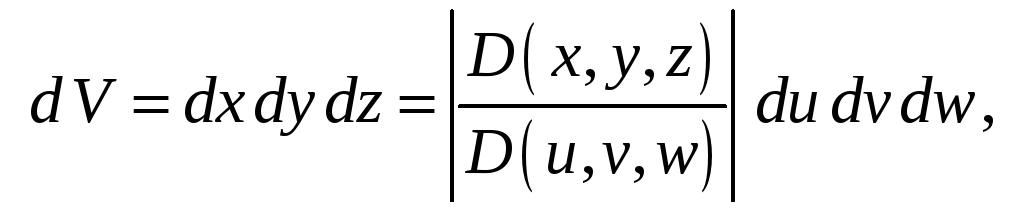
Здесь и ─ области изменения соответственно переменных и .

Для вычисления тройного интеграла следует

1) заменить на их выражения в криволинейной системе координат,

, ;

2) заменить область изменения переменных на область изменения переменных .

Замечание. Иногда удобнее вычислить не якобиан а якобиан . Тогда искомый якобиан .

Пример 3. Вычислить объем параллелепипеда, ограниченного плоскостями

Решение. Введем новые переменные

и вычислим якобиан

Тогда искомый объем равен

10.3 Тройной интеграл в цилиндрических координатах

Положение точки в пространстве можно охарактеризовать с помощью цилиндрических координат , где полярные координаты проекции точки на плоскость аппликата точки . Поэтому аналогично полярной системе координат

Вычислим якобиан .

Тогда элемент объема в цилиндрических координатах

.

Для вычисления тройного интеграла следует

1) заменить на их выражения в цилиндрической системе координат,

, ;

2) заменить область изменения переменных на область изменения переменных .

Замечания

1). К цилиндрическим координатам целесообразно переходить, когда уравнение

поверхностей, ограничивающих тело, содержит .

2). Внутреннее интегрирование обычно удобно вести по .

Пример 4. Вычислить массу тела, ограниченного поверхностями , если плотность

Решение. Поверхность строим методом сечений:

Получаем параболоид (рис. 4).

Поверхность также строим методом сечений

Получаем конус (рис. 4).

В цилиндрической системе координат уравнения этих поверхностей имеют более простой вид: Решив систему из этих двух уравнений, найдем пересечение этих поверхностей ─ окружность

Вычислим массу тела, используя для вычисления интеграла цилиндрическую систему координат, учитывая, что , внутреннее интегрирование ─ по , причем на прямой, параллельной оси , меняется от на конусе до на поверхности параболоида (рис. 4):

Оглавление

10. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ТРОЙНОЙ ИНТЕГРАЛ, ЕГО ОСНОВНЫЕ СВОЙСТВА. 1

10.1. Тройной интеграл в прямоугольной системе 1

10.2 Тройной интеграл в криволинейной системе 6

10.3 Тройной интеграл в цилиндрических координатах 7

Оглавление 10