
Математика ЗО от Белоусовой / Математический анализ, лекции 2 семестр / Лекция 17
.doc17. Лекционное занятие. СОЛЕНОИДАЛЬНОЕ ПОЛЕ.
Поле
![]() называют соленоидальным, если оно
является полем ротора некоторой векторной
функции
называют соленоидальным, если оно
является полем ротора некоторой векторной
функции
![]() ,
т.е.
,
т.е.
![]() ;
при этом вектор
;
при этом вектор
![]() называют векторным потенциалом поля
называют векторным потенциалом поля
![]() .
.
17.1 Свойства соленоидального поля
1). Поле
![]() является соленоидальным
тогда и только тогда, когда
является соленоидальным
тогда и только тогда, когда
![]() .
.
2). В соленоидальном поле поток через замкнутую поверхность, не содержащую внутри особых точек поля, равен нулю.
3). В соленоидальном поле потоки через замкнутые поверхности, окружающие все особые точки поля, равны между собой.
4). В соленоидальном поле поток через любое поперечное сечение векторной трубки сохраняет постоянное значение (называемое интенсивностью трубки).
Проверим эти свойства.
-
Пусть поле
 ─ соленоидально, т.е.
─ соленоидально, т.е.
 ;
;
тогда

можно показать, что справедливо и
обратное: если
![]() ,
то
,
то
![]() .
.
-
В
 соленоидальном поле
соленоидальном поле
 и потому по формуле Остроградского
поток через замкнутую поверхность, не
содержащую внутри особых точек поля,
и потому по формуле Остроградского
поток через замкнутую поверхность, не
содержащую внутри особых точек поля,
![]() .
.
-
Пусть
 ─ поверхности, окружающие все особые
точки поля; их ориентация указана на
рис. 1. Обозначим через
─ поверхности, окружающие все особые
точки поля; их ориентация указана на
рис. 1. Обозначим через
 ─ тело с границей
─ тело с границей
 ;
внутри тела
;
внутри тела
 поле определено,
поле определено,
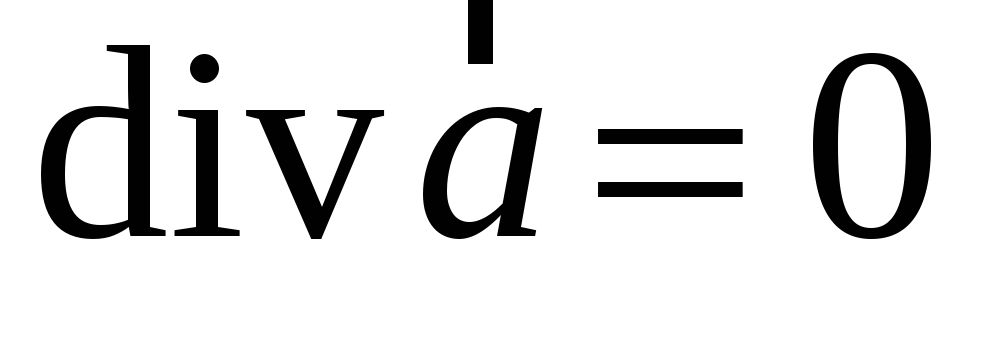 ,
и потому по формуле Остроградского
,
и потому по формуле Остроградского
![]() .
.
С другой стороны,
![]() и следовательно,
и следовательно,![]() .
.
4
Рис. 2
![]() поперечные
сечения векторной трубки с указанной
на рис. 79 ориентацией;
поперечные
сечения векторной трубки с указанной
на рис. 79 ориентацией;
![]() поверхность
векторной трубки, состоящая из векторных
линий;
поверхность
векторной трубки, состоящая из векторных
линий;
![]() граница
тела
граница
тела
![]() .
.
Вычислим поток поля через поверхность
![]() :
с одной стороны, по
свойству 2) этот поток равен нулю; с
другой стороны,
:
с одной стороны, по
свойству 2) этот поток равен нулю; с
другой стороны,
![]() ,
а
,
а
 ,
т.к.
,
т.к.
![]() состоит из векторных линий, значит,
вектор поля
состоит из векторных линий, значит,
вектор поля
![]() направлен по касательной к векторной
линии, т.е.
направлен по касательной к векторной
линии, т.е.
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() .
.
Пример 1.
Найти поток поля напряженностей
![]() ,
создаваемого зарядом
,
создаваемого зарядом
![]() ,
через произвольную замкнутую поверхность
,
через произвольную замкнутую поверхность
![]() .
.
Решение.
Дивергенция поля
![]() равна нулю, потому
поле напряженностей
равна нулю, потому
поле напряженностей
![]() является соленоидальным всюду, где
определено (т.е. в точках
является соленоидальным всюду, где
определено (т.е. в точках
![]() ,
отличных от начала координат).
,
отличных от начала координат).
Тогда по свойству 2) соленоидального поля поток поля через любую замкнутую поверхность, не окружающую начала координат, равен нулю.
По свойству 3) соленоидального поля
поток поля через замкнутую поверхность,
окружающую начало координат, равен,
например, потоку этого поля через сферу
с центром в начале координат и равен
![]() .
.
17.2 Отыскание векторного потенциала
Прежде всего отметим, что векторный
потенциал
![]() соленоидального поля
соленоидального поля
![]() определяется с точностью до градиента
произвольной функции.
определяется с точностью до градиента
произвольной функции.
Действительно, так
как поле
![]() потенциально,
то
потенциально,
то
![]() и потому
и потому
![]() ;
;
значит, вектор
![]() также является векторным потенциалом
поля
также является векторным потенциалом
поля
![]() .
Поэтому подбором вектора
.
Поэтому подбором вектора
![]() можно добиться того, чтобы одна из
координат векторного потенциала
можно добиться того, чтобы одна из
координат векторного потенциала
![]() равнялась нулю, т.е. можно искать векторный
потенциал, например, в виде
равнялась нулю, т.е. можно искать векторный
потенциал, например, в виде
![]() .
Тогда
.
Тогда
 .
.
Так как
![]() ,
то получим систему уравнений
,
то получим систему уравнений
 .
.
Проинтегрируем первое и второе из
равенств по
![]() :
:
![]() ;
;
здесь
![]() произвольные
функции, не зависящие от переменной
интегрирования
произвольные
функции, не зависящие от переменной
интегрирования
![]() .
Подставляя найденные
.
Подставляя найденные
![]() в третье из равенств, найдем функции
в третье из равенств, найдем функции
![]()
Пример 2. Проверить
соленоидальность поля
![]() и найти его векторный потенциал.
и найти его векторный потенциал.
Решение. Так как
 ,
то поле соленоидально, т.е.
,
то поле соленоидально, т.е.
![]() .
Будем искать векторный потенциал в виде
.
Будем искать векторный потенциал в виде
![]() .
Тогда
.
Тогда
 .
.
Так как
![]() то получим систему уравнений
то получим систему уравнений
 .
.
Проинтегрируем первое и второе из этих
равенств по
![]() :
:
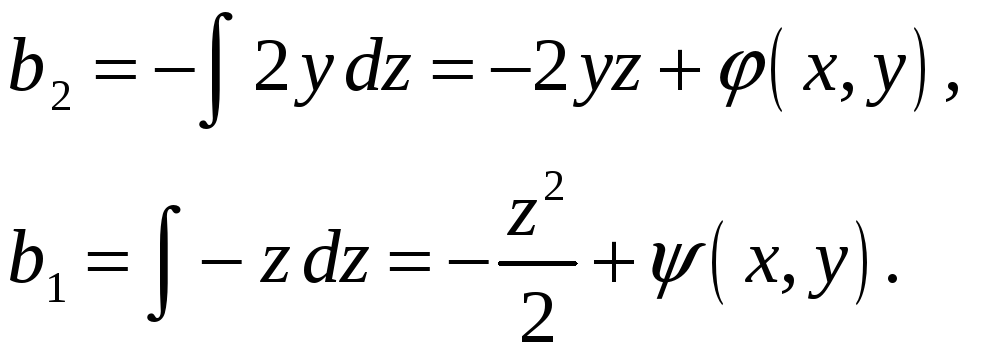
Подставив эти выражения для
![]() в третье из равенств, получим
в третье из равенств, получим
 .
.
В частности, можно взять
![]() .
Тогда векторный потенциал
.
Тогда векторный потенциал
 .
.
17.3. Гармонические поля
17.3.1 Гармоническое скалярное поле
Скалярное поле
![]() называется гармоническим, если функция
называется гармоническим, если функция
![]() удовлетворяет уравнению Лапласа
удовлетворяет уравнению Лапласа
![]() .
.
Правая часть
уравнения Лапласа называется оператором
Лапласа и обозначается
![]() .
Оператор Лапласа будет использован в
дальнейшем при решении задач математической
физики (задач колебания, теплопроводности,
диффузии).
.
Оператор Лапласа будет использован в
дальнейшем при решении задач математической
физики (задач колебания, теплопроводности,
диффузии).
В прямоугольной системе координат
![]()
и уравнение Лапласа примет вид
![]() .
.
Пример 1. Показать, что поле
![]() является гармоническим в пространстве
является гармоническим в пространстве
![]() ,
а поле
,
а поле
![]() является гармоническим в пространстве
является гармоническим в пространстве
![]() .
.
Решение.
1). По свойствам градиента
 .
.
По свойствам дивергенции
 .
.
Учитывая, что
![]() в пространстве
в пространстве
![]() ,
,
![]() ,
получим:
,
получим:
 .
.
2). В пространстве
![]() для поля
для поля
![]() имеем:
имеем:
![]()
 .
.
17.3.2 Гармоническое векторное поле
Векторное поле
![]() ,
являющееся одновременно и потенциальным,
и соленоидальным, называется гармоническим
векторным полем.
,
являющееся одновременно и потенциальным,
и соленоидальным, называется гармоническим
векторным полем.
Отметим следующие свойства гармонического векторного поля.
1). Гармоническое векторное поле обладает скалярным и векторным потенциалом.
2). Скалярный потенциал
![]() является функцией гармонической.
является функцией гармонической.
3). Для гармонического векторного поля
![]() его координаты
его координаты
![]() являются функциями гармоническими.
являются функциями гармоническими.
Проверим эти свойства.
1). Первое свойство следует из определения, т.к. потенциальное поле обладает скалярным потенциалом, а соленоидальное поле обладает векторным потенциалом.
2). Так как гармоническое поле
![]() потенциально, то оно обладает скалярным
потенциалом
потенциально, то оно обладает скалярным
потенциалом
![]() и представимо в виде
и представимо в виде
![]() .
С другой стороны, гармоническое поле
является соленоидальным, поэтому
.
С другой стороны, гармоническое поле
является соленоидальным, поэтому
![]() .
.
Таким образом, потенциал
![]() гармонического поля
гармонического поля
![]() удовлетворяет уравнению Лапласа
и является гармонической функцией.
удовлетворяет уравнению Лапласа
и является гармонической функцией.
3). Для гармонического
векторного поля
![]() в силу его потенциальности
в силу его потенциальности
![]() ,
т.е.
,
т.е.
 или
или

В силу соленоидальности гармонического
векторного поля
![]() ,
т.е.
,
т.е.
 .
Продифференцируем это равенство по
.
Продифференцируем это равенство по
![]()

и воспользуемся вторым и третьим из равенств (12.5):
 или
или
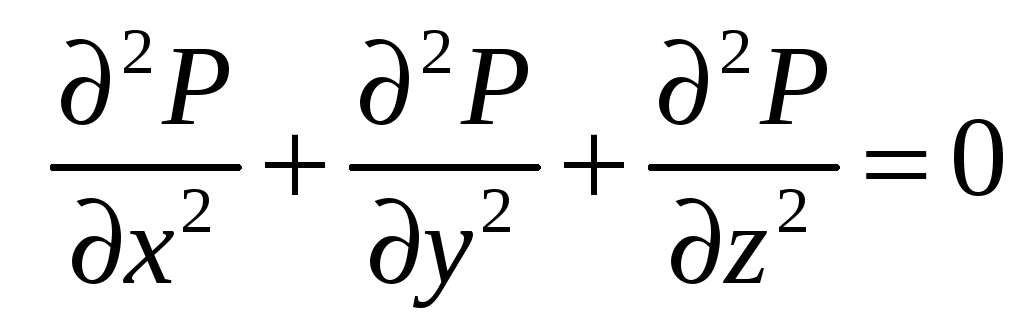 .
.
Это значит, что функция
![]() является гармонической. Аналогично
можно показать, что функции
является гармонической. Аналогично
можно показать, что функции
![]() являются гармоническими.
являются гармоническими.
17.4 Повторные операции теории поля
1). Рассмотрим скалярное поле
![]() .
В нем определен вектор
.
В нем определен вектор
![]() .
.
В векторном поле
![]() определены понятия дивергенции и ротора
определены понятия дивергенции и ротора
![]() .
.
2). Рассмотрим векторное поле
![]() .
В нем определены скаляр
.
В нем определены скаляр
![]() и вектор
и вектор
![]() .
Для скалярного поля
.
Для скалярного поля
![]() определено понятие градиента
определено понятие градиента
![]() .
.
Для векторного поля
![]() определены понятия дивергенции и ротора
определены понятия дивергенции и ротора
![]() ,
,
![]() .
.
Рассмотрим каждую из этих операций более подробно.
Выражение![]() есть оператор Лапласа
есть оператор Лапласа
![]() ;
;
Так как поле
![]() является потенциальным, а в потенциальном
поле ротор равен нулю, то
является потенциальным, а в потенциальном
поле ротор равен нулю, то
![]() .
.
Так как поле
![]() является соленоидальным, а в соленоидальном
поле дивергенция равна нулю, то
является соленоидальным, а в соленоидальном
поле дивергенция равна нулю, то
![]() .
.
Выражения
![]() и
и
![]() используются в электродинамике и связаны
соотношением (которое будет установлено
позже)
используются в электродинамике и связаны
соотношением (которое будет установлено
позже)
![]() .
.
Здесь
![]() для вектора
для вектора
![]() понимают как
понимают как
![]()
Оглавление
17. Лекционное занятие. СОЛЕНОИДАЛЬНОЕ ПОЛЕ. 1
17.1 Свойства соленоидального поля 1
17.2 Отыскание векторного потенциала 3
17.3. Гармонические поля 6
17.3.1 Гармоническое скалярное поле 6
17.3.2 Гармоническое векторное поле 7
17.4 Повторные операции теории поля 8
Оглавление 10
