
Математика ЗО от Белоусовой / Математический анализ, лекции 2 семестр / Лекция 1
.docx-
Лекционное занятие. Первообразная, ее свойства. Неопределенный интеграл, его свойства.
-
Определение первообразной функции.
Ранее
рассматривалось понятие производной
функции, ее
геометрический смысл,
свойства, правила нахождения. Во многих
технических задачах требуется решение
обратной задачи: отыскание функции по
заданной ее производной функции.
Например,
задача об определении закона
прямолинейного движения
 материальной точки по заданной ее
скорости
материальной точки по заданной ее
скорости
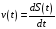 .
.
Решение сформулированной задачи основано на понятии первообразной функции.
Определение.
Функция
 ,
определенная на промежутке
,
определенная на промежутке
 ,
называется первообразной
функцией
(или просто первообразной)
для функции
,
называется первообразной
функцией
(или просто первообразной)
для функции
 на
на
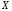 ,
если в любой точке этого промежутка
функция
,
если в любой точке этого промежутка
функция
 дифференцируема и имеет производную
дифференцируема и имеет производную
 ,
равную
,
равную
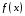 :
:
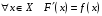 .
.
Пример.
Функция
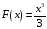 является первообразной для
является первообразной для
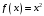 на
на
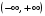 ,
так как для любого
,
так как для любого
 имеем
имеем
 .
.
Для
одной и той же функции существует
бесконечное множество первообразных.
Например, для
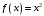 первообразными на
первообразными на
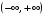 являются также функции
являются также функции
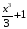 ,
,
 и вообще
и вообще
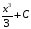 ,
где
,
где
 – произвольное число, поскольку
– произвольное число, поскольку
 для любого
для любого
 .
.
Аналогичные
рассуждения верны и для первообразной
произвольной функции
 .
.
Свойства первообразных описываются легко проверяемыми теоремами.
Теорема
1.
Если
 – первообразная для функции
– первообразная для функции
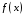 на
на
 ,
то функция
,
то функция
 ,
где
,
где
 – произвольное число, также является
первообразной для
– произвольное число, также является
первообразной для
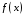 на
на
 .
.
Теорема
2.
Если
 и
и
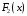 – произвольные первообразные для
– произвольные первообразные для
 на
на
 ,
то значение разности этих первообразных
в каждой точке есть одно и то же число,
т.е.
,
то значение разности этих первообразных
в каждой точке есть одно и то же число,
т.е.
 на
на
 ,
где
,
где
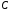 – некоторое число.
– некоторое число.
Теоремы
1 и 2 показывают, что если функция имеет
первообразную
 ,
то множество функций
,
то множество функций
 ,
где
,
где
 и
и
 ,
образует множество всех
первообразных для функции
,
образует множество всех
первообразных для функции
 на
на
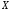 .
.
Для
 множество всех первообразных есть
множество функций
множество всех первообразных есть
множество функций
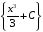 ,
,
 ,
,
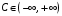 .
.
Определение.
Множество всех
первообразных для функции
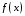 на промежутке
на промежутке
 называется неопределенным
интегралом
функции
называется неопределенным
интегралом
функции
 на
на
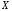 и обозначается символом
и обозначается символом
 .
.
Выражение
 называется подынтегральным выражением,
называется подынтегральным выражением,
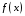 – подынтегральной функцией,
– подынтегральной функцией,
 – переменной интегрирования,
– переменной интегрирования,
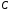 – произвольной постоянной. Процедуру
отыскания
неопределенного интеграла
функции называют интегрированием
функции (будем говорить, что "интеграл
вычисляется").
– произвольной постоянной. Процедуру
отыскания
неопределенного интеграла
функции называют интегрированием
функции (будем говорить, что "интеграл
вычисляется").
Если
 – какая-либо первообразная функции
– какая-либо первообразная функции
 на
на
 ,
то в силу определения неопределенного
интеграла и свойств первообразных имеем
,
то в силу определения неопределенного
интеграла и свойств первообразных имеем
 ,
,
 ,
,
 .
.
Для краткости это равенство записывается обычно в виде
 .
.
Пример.
Проверить формулу
 ,
,
 или
или
 .
.
Решение.
Используя определение абсолютной
величины
 ,
можем записать
,
можем записать

На
интервале
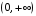 имеем
имеем
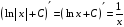 ,
поэтому для функции
,
поэтому для функции
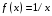 на
на
 функция
функция
 является первообразной.
является первообразной.
На
интервале
 имеем
имеем
 ,
поэтому для функции
,
поэтому для функции
 на
на
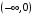 первообразная имеет вид
первообразная имеет вид
 .
.
1.2 Свойства неопределенного интеграла
Свойства неопределенного интеграла базируются на свойствах дифференциала функции.
Напомним,
что если
 – дифференцируемая в точке
– дифференцируемая в точке
 функция, то произведение
функция, то произведение
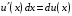
является
дифференциалом функции
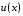 в точке
в точке
 соответственно приращению аргумента
соответственно приращению аргумента
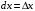 .
.
Для
дифференцируемых функций
 и
и
 правила действий над их дифференциалами
аналогичны правилам вычисления
производных (здесь и везде далее
правила действий над их дифференциалами
аналогичны правилам вычисления
производных (здесь и везде далее
 – произвольное число), а именно:
– произвольное число), а именно:
 ;
;
 ;
;  ;
;
 ;
; 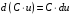 ;
;
 .
.
Для
первообразной
 функции
функции
 из соотношения
из соотношения
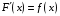 ,
,
 имеем
имеем
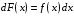 или
или
 – подведение функции
– подведение функции
 под дифференциал.
под дифференциал.
Используя указанные равенства, получаем следующие свойства неопределенного интеграла.
Свойство
1.
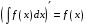 ,
,
т.е.
производная неопределенного интеграла
(производная каждой функции множества
всех первообразных
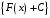 )
равна подынтегральной функции.
)
равна подынтегральной функции.
Свойство
2.
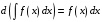 ,
,
т.е. дифференциал неопределенного интеграла (дифференциал каждой функции множества всех первообразных) равен подынтегральному выражению.
Иначе,
знаки дифференциала и интеграла взаимно
уничтожаются, если знак "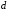 "
стоит перед знаком "
"
стоит перед знаком " ".
".
Свойство
3.
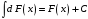 ,
,
т.е.
неопределенный интеграл от дифференциала
какой-либо функции равен сумме этой
функции и произвольного числа
 .
Иначе, если знак "
.
Иначе, если знак " "
стоит рядом и перед знаком "
"
стоит рядом и перед знаком " ",
то эти знаки тоже взаимно уничтожаются,
причем к функции
",
то эти знаки тоже взаимно уничтожаются,
причем к функции
 прибавляется произвольное число
прибавляется произвольное число
 .
.
Свойство
4.
 – аддитивность по функции операции
интегрирования, т.е. неопределенный
интеграл от суммы функций равен сумме
неопределенных интегралов от этих
функций (предполагается, что все
участвующие в равенстве интегралы
существуют). При этом, если
– аддитивность по функции операции
интегрирования, т.е. неопределенный
интеграл от суммы функций равен сумме
неопределенных интегралов от этих
функций (предполагается, что все
участвующие в равенстве интегралы
существуют). При этом, если
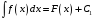 и
и
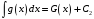 ,
то записывают
,
то записывают
 ,
объединяя
,
объединяя
 и
и
 в одну произвольную постоянную
в одну произвольную постоянную
 .
.
Свойство 4 верно для суммы конечного множества слагаемых.
Свойство
5.
 ,
,
 ,
,
 –
–
Однородность операции интегрирования, т.е. при вычислении неопределенного интеграла постоянный ненулевой множитель можно выносить за знак интеграла (соответственно можно вносить под знак интеграла).
Пример.
Вычислить интеграл
 .
.
Решение.
В силу свойства 4 имеем
 .
.
Согласно
свойству 5 выполняются равенства:
 ,
,
 ,
,
 .
.
Из
ранее рассмотренных примеров имеем
 и
и
 .
Поэтому
.
Поэтому
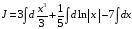 .
Отсюда в силу свойства 3
.
Отсюда в силу свойства 3
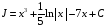 .
.
Свойство
6.
Пусть
 – первообразная для
– первообразная для
 на
на
 ;
функция
;
функция
 – произвольная дифференцируемая на
– произвольная дифференцируемая на
 функция, множество значений которой
совпадает с
функция, множество значений которой
совпадает с
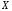 .
Тогда равенство
.
Тогда равенство
 сохраняется, если заменить в обеих
частях его переменную интегрирования
сохраняется, если заменить в обеих
частях его переменную интегрирования
 функцией
функцией

 ,
,
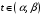 .
.
В
самом деле, вычисляя дифференциал
сложной функции
 ,
получим выражение
,
получим выражение
 ,
,
совпадающее с подынтегральным выражением интеграла, что доказывает справедливость формулы.
Свойство 6 называют обычно свойством инвариантности формул интегрирования и используют при вычислении интегралов (замена переменной).
Пример.
Равенство
 в силу свойства 6 можно записать в виде
в силу свойства 6 можно записать в виде
 ,
где
,
где
 (или
(или
 )
– произвольная дифференцируемая
функция, и использовать в качестве
формулы для вычисления многих интегралов.
Например,
)
– произвольная дифференцируемая
функция, и использовать в качестве
формулы для вычисления многих интегралов.
Например,
 ,
,
 ,
,
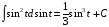 ,
,
 .
.
Заметим,
что более общая формула
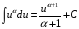 (
( – произвольное число,
– произвольное число,
 )
следует из равенства
)
следует из равенства
 ,
если использовать свойство 6.
,
если использовать свойство 6.
Аналогично
из каждой формулы дифференцирования
элементарной функции
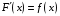 путем ее обращения получается
"интегральная" формула
путем ее обращения получается
"интегральная" формула
 .
Подобные формулы составляют таблицу
основных интегралов, которые называются
для краткости "табличными".
.
Подобные формулы составляют таблицу
основных интегралов, которые называются
для краткости "табличными".
В практике вычисления неопределенных интегралов обычно пользуются специальными справочниками.
1.3 Таблица неопределенных интегралов
1.
 ,
,
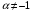 . 2.
. 2.
 .
.
3.
 ,
,  .
.
4.
 . 5.
. 5.
 .
.
6.
 . 7.
. 7.
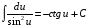 .
.
8.
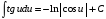 . 9.
. 9.
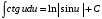 .
.
10.
 .
.
11.
 .
.
12.
 . 13.
. 13.
 .
.
14.
 .
.
15.
 .
.
Все формулы таблицы интегралов можно проверить, опираясь на определение неопределенного интеграла. Например, справедливость формулы 12 следует из равенств
 .
.
1.4 Непосредственное интегрирование с помощью табличных интегралов
Сведение
исходного интеграла к табличному тесно
связано с операцией подведения функции
под знак дифференциала:
 .
Функция
.
Функция
 – какая-то первообразная для
– какая-то первообразная для
 и ее подбирают, используя формулы
дифференцирования и правила
дифференцирования. Например, имеем (для
и ее подбирают, используя формулы
дифференцирования и правила
дифференцирования. Например, имеем (для
 из ОДЗ функций):
из ОДЗ функций):
 ;
;  ;
;
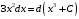 ;
; 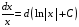 ;
;
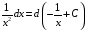 ;
;  ;
;
 ;
;
 ;
; 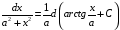 ;
;
 ;
;  и т.д.
и т.д.
Оглавление
1.Лекционное занятие. Первообразная, ее свойства. Неопределенный интеграл, его свойства. 1
1.1Определение первообразной функции. 1
1.2 Свойства неопределенного интеграла 5
1.3 Таблица неопределенных интегралов 11
1.4 Непосредственное интегрирование с помощью табличных интегралов 13
