14. Лекционное занятие. ФОРМУЛА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ

Поток векторного поля через замкнутую поверхность удобно вычислять по формуле Остроградского с помощью дивергенции поля :

где .

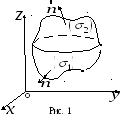В этой формуле ─ тело, ограниченное замкнутой поверхностью ;поверхность ориентирована внешней нормалью; функции , , непрерывны вместе со своими частными производными.

Вывод формулы проведем для случая, когда поверхность состоит (рис. 1) из поверхности с уравнением и поверхности с уравнением .

Запишем формулу Остроградского в координатной форме

.

Покажем сначала, что . Действительно,

.

С другой стороны, .

На поверхности : ; , так как ;

на поверхности : ; , так как ;

поэтому

.

Получившееся выражение равно правой части формулы, значит

.

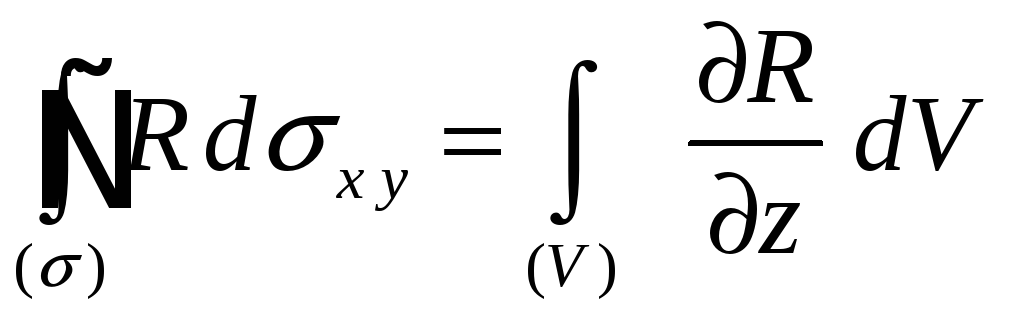Аналогично можно показать, что

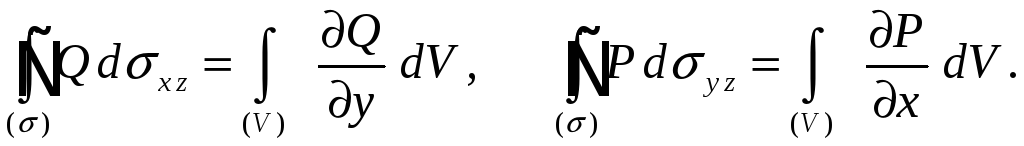
Складывая равенства, получим формулу Остроградского.

Пример 1. Вычислить поток поля через поверхность пирамиды, ограниченную плоскостью и координатными плоскостями.

Решение. Так как поверхность замкнутая, то воспользуемся формулой Остроградского

.

Пример 2 . Вычислить поток жидкости, текущей со скоростью , через боковую поверхность конуса в направлении внешней нормали (рис. 2).

Р

ешение. Поток через боковую поверхность конуса удобно вычислить как разность потока через полную поверхность и потока через основание. Поток через полную поверхность вычислим по формуле Остроградского

о

.

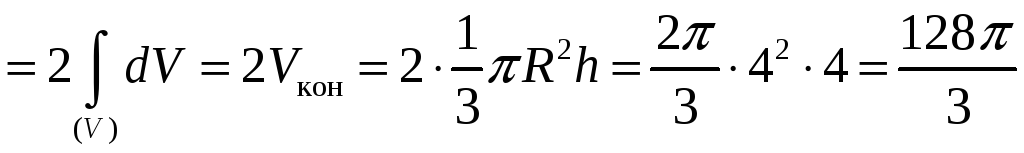Поток жидкости через основание конуса вычислим по формуле .

Учтем, что единичный вектор нормали к основанию конуса равен . Поэтому . На основании конуса , значит, и

Здесь ─ площадь основания, т. е. площадь круга радиусом 4. Следовательно,

.

Так как , то через боковую поверхность конуса в направлении внешней нормали течет жидкости меньше, чем в противоположном направлении.

Остановимся более подробно на свойствах дивергенции.

14.1 Инвариантное определение дивергенции

Рассмотрим точку (рис. 3), окружим ее замкнутой поверхностью и вычислим поток поля через эту поверхность по формуле Остроградского

.

Применяя к тройному интегралу теорему о среднем, получим

или .

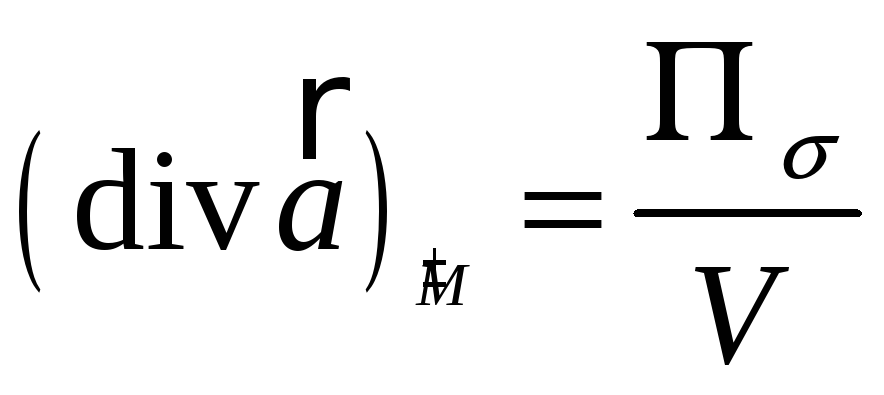Здесь есть некоторая точка из области . В последнем равенстве перейдем к пределу, стягивая область в точку (при этом точка будет стремиться к точке ). Запишем результат предельного перехода:

Мы получили инвариантное (т.е. независящее от системы координат) определение дивергенции. Первоначальное определение дивергенции

было введено для прямоугольной системы координат.

14.2 Физический смысл дивергенции

Пусть векторное поле есть поле скоростей жидкости. Величина потока равна разности между количеством жидкости, вытекающей из области , и количеством жидкости, втекающей в эту область. Если , то из области жидкости вытекает больше, чем втекает. Это означает, что в области имеются источники, питающие поток жидкости. Величина определяет количество жидкости, возникающей в единицу времени в единице объема. Ее называют средней мощностью источников в области . Величину

называют мощностью источника в точке .

Если , то в область втекает жидкости больше, чем вытекает, т. е. в области имеются стоки со средней мощностью . Величина

есть мощность стока в точке . Итак,

1) если , то в точке имеется источник мощности ,

2) если , то в точке имеется сток мощности ,

3) если , то в точке отсутствуют и источник, и сток.

14.3 Дифференциальные свойства дивергенции

1) , или постоянный вектор),

2) , или радиус-вектор),

3) или

4) или

скалярное поле, векторное поле),

5) или константа),

6) или ( постоянный вектор).

Проверим эти свойства:

1)

2)

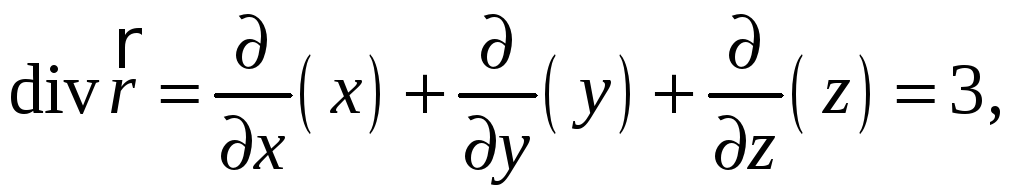
свойство 3) проверяется так же, как свойство 4),

свойство 5) есть следствие свойства 4) при ,

свойство 6) есть следствие свойства 4) при .

Пример 1. Доказать, что .

Решение. По свойству 4) дивергенции ;

по свойствам градиента . Тогда

.

Пример 2. Доказать, что дивергенция поля напряженностей, создаваемого зарядом , равна нулю.

Решение. Поле напряженностей, создаваемое зарядом, есть поле . Из предыдущего примера при следует, что

.

14.4 Линейный интеграл и циркуляция векторного поля

Задача о работе силы

П

усть задано поле сил , под действием которых материальная точка движется по кривой от точки к точке . Вычислим совершаемую при этом работу. Для этого разобьем линию на частей точками с радиус-векторами (рис. 66). Рассмотрим вектор перемещения

и вектор силы . Их скалярное произведение приближенно равно работе силы вдоль дуги , т. е.

.

Вычислим работу вдоль всей линии :

.

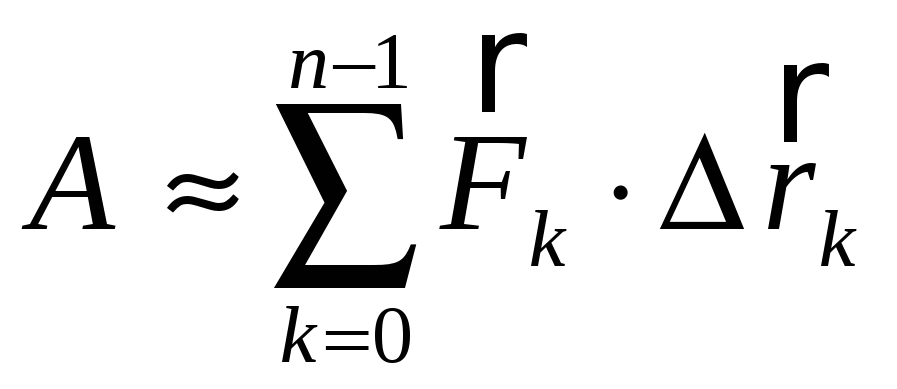Это равенство будет тем точнее, чем меньше длины векторов . Максимальную из этих длин обозначим и, переходя к пределу при , определим точное значение работы

.

Этот предел обозначают и называют линейным интегралом поля по дуге или криволинейным интегралом второго рода.

14.5. Понятие линейного интеграла и его свойства

Отвлекаясь от физического содержания рассмотренной задачи, аналогичным образом вводят понятие линейного интеграла произвольного поля (риc. 4):

,

где ─ точки разбиения дуги , .

Отметим три свойства линейного интеграла:

1) (свойство линейности),

2) (свойство аддитивности),

3) ,

т. е. при изменении направления обхода кривой линейный интеграл меняет знак, т. к. векторы меняют свое направление на противоположное.

Выразив скалярное произведение векторов и через их координаты, получим

Выражение в скобки не заключают, хотя знак интеграла относится ко всему этому выражению. В формуле функции есть функции точки или ее координат . Интеграл называют векторной формой, а интеграл ─ координатной формой записи линейного интеграла.

В тех случаях, когда линейный интеграл поля берется по замкнутой кривой , он называется циркуляцией поля по кривой и обозначается так:

Приняты и другие обозначения циркуляции:

Оглавление

14. Лекционное занятие. ФОРМУЛА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ 1

14.1 Инвариантное определение дивергенции 3

14.2 Физический смысл дивергенции 3

14.3 Дифференциальные свойства дивергенции 4

14.4 Линейный интеграл и циркуляция векторного поля 5

Задача о работе силы 5

14.5. Понятие линейного интеграла и его свойства 6

Оглавление 7