15.Лекционное занятие. Вычисление линейного интеграла.

Правило вычисления линейных интегралов в следующих двух случаях.

1). Для вычисления интеграла по линии,заданной уравнениями, следует:

а) записать интеграл в координатной форме

б) заменить в функцияхсоответственно на,

в) заменить соответственно на,

г) найти интервал изменения параметра и вычислить получившийся определенный интеграл по этому интервалу.

2). Для вычисления интеграла по плоской линиис уравнениемследует:

а) записать интеграл в координатной форме,

б) заменить в функцияхна,

в) заменить на,

г) вычислить получившийся определенный интеграл по отрезку .

3). В случае центрального поля следует учесть, что; дифференцируя это равенство, получими

т.е. линейный интеграл поля сведен к определенному интегралу.

Пример 1.Вычислить работу силыпо прямолинейному перемещению из точкив точку.

Решение. Работа силывычисляется по формуле

.

Для вычисления этого интеграла составим уравнение прямой :

.

Отсюда

Найдем значение параметра , соответствующее точке. Для этого подставим абсциссуточкив формулу. Получим. Аналогично найдем. Заменяя в интегралеих выражениями, получим

.

Пример 2.Найти циркуляцию полявдоль линии, где─ дуга параболы,─ ломаная (рис. 1).

Решение. Циркуляцию поля вычислим по формуле

.

На отрезке имеем. Поэтому

0

.

На отрезке имеем. Поэтому

.

На дуге имеем. Поэтому

.

Окончательно, .

Пример 3. Вычислить циркуляцию поля по окружностирадиусомс центром в начале координат, ориентированной против часовой стрелки.

Решение. Циркуляция полявычисляется по формуле

.

Д

ля вычисления этого интеграла запишем параметрические уравнения окружности:.

Т

Рис. 2

огда,; уголпри движении против часовой стрелки меняется отдо(рис. 2). Поэтому.

15.1. Формулы Грина и Стокса. Ротор поля

Часто удобно вычислять циркуляцию плоского поля по формуле Грина, а циркуляцию пространственного поля

─ по формуле Стокса.

Если при обходе замкнутого контура ограниченная область остается слева, то направление обхода называют положительным. Обход в противоположном направлении называют отрицательным.

Теорема 1. Пусть функции и их частные производные непрерывны в областис положительно ориентированной границей. Тогда имеет место следующая формула Грина:

.

Доказательство проведем для области, описываемой неравенствами(рис. 3).

Сначала проверим равенство

.

Сведем криволинейный интеграл к определенному интегралу, подставляяна линииина линии:

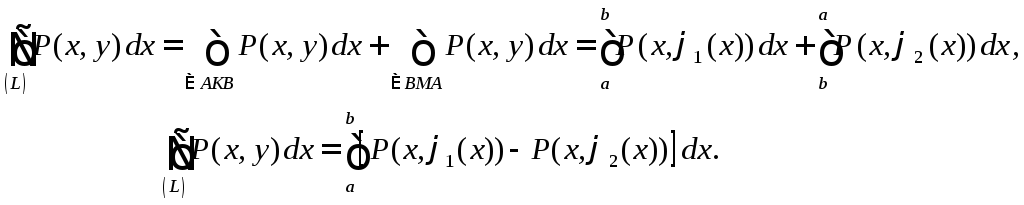
Теперь преобразуем двойной интеграл, сведя его сначала к повторному, а затем к определенному интегралу:

.

И криволинейный, и двойной интегралы из формулы (11.6) равны одному и тому же определенному интегралу и, следовательно, равны между собой. Аналогично проверяется равенство

.

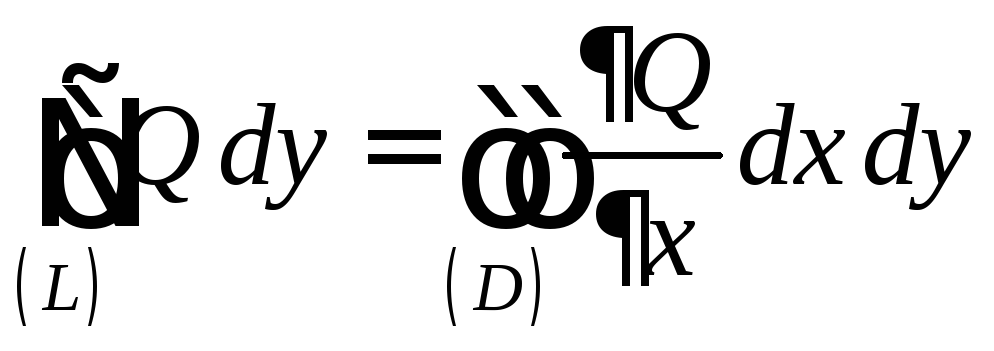Складывая равенства, получим формулу Грина.

Замечание. Нарушение условий теоремы Грина может привести к неверным результатам. Например, для поля нетрудно проверить, что

,

но циркуляция поля по окружности с центром в начале координат отлична от нуля,. В этом примере нарушены условия теоремы Грина, т.к. внутри контурасодержится точка, в которой функциине определены.

Пример 4. Используя формулу Грина, вычислить циркуляцию полявдоль линии(рис. 3).

Решение. Вычислим циркуляцию , используя формулу Грина для:.

Для обобщения формулы Грина на пространственный случай введем понятие ротора векторного поля .

Ротором векторного поля называется вектор

.

При вычислении следует разложить определитель по элементам первой строки. Учитывая, что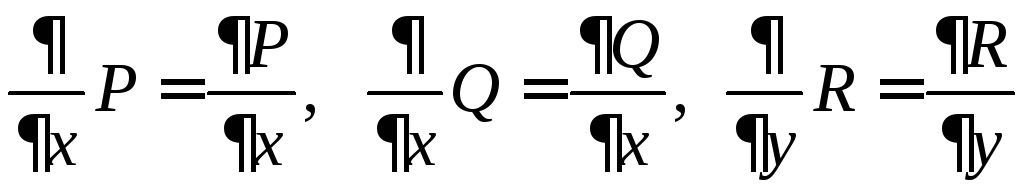и т. д., получим

.

Понятие ротора позволяет удобно вычислять циркуляцию векторного поля, опираясь на следующую теорему (доказательство теоремы опустим).

Теорема 2. Пусть функции и их частные производные непрерывны на ориентированной поверхности, натянутой на контур, причем ориентации контураи поверхностисогласованы. Тогда имеет место следующая формула Стокса:

.

Вэтой формуле ориентации контураи поверхностисогласованы, т. е.,глядя с конца выбранных нормальных векторов поверхности , обход контуравиден против часовой стрелки (рис. 4).

Итак, по формуле Стокса циркуляция поля по контуруравна потоку ротора полячерез поверхность, натянутую на контур.

Пример 5. Для полянайти его циркуляцию по окружности,лежащей в плоскости и ориентированной против часовой стрелки, если смотреть с конца оси(рис. 5).

Решение. Циркуляция поля вычисляется по формуле.Непосредственное вычисление этого интеграла достаточно трудоемко. Посмотрим, облегчит ли вычисление циркуляции применение формулы Стокса. Для этого вычислим ротор

По формуле Стокса имеем:

.

В качестве поверхности , натянутой на окружность, возьмем круг, ограниченный этой окружностью. Нормальный вектор к этой поверхности направлен вдоль оси, т.е.; скалярное произведение;

.

Остановимся более подробно на свойствах ротора.