3. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ

3.1 Интегрирование тригонометрических функций

Случай 1. ,где хотя бы одно из чисел положительное нечетное число. В этом случае следует отделить от нечетной степени (или ) одну степень и подвести ее под знак дифференциала.

Пример 1. Найти .

Подынтегральная функция содержит в нечетной положительной степени. Поэтому отделим в числителе и воспользуемся тем, что , а . Тогда

Пример 2. Найти .

Подынтегральная функция содержит в нечетной положительной степени. Поэтому отделим и воспользуемся тем, что . Тогда

.

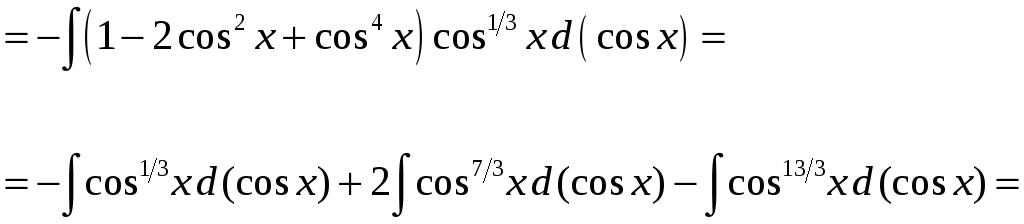
Случай 2. , где четные неотрицательные числа. В этом случае следует понизить степень, используя формулы удвоения угла:

, , .

Пример 3. Найти .

Подынтегральная функция содержит и в четной степени. Поэтому понизим степени, используя формулы:

Пример 4. Найти .

Подынтегральная функция содержит в четной степени. Поэтому воспользуемся одной из формул и формулой для куба суммы:

Тогда . При этом

,

Итак,

.

Случай 3. , где целые числа и хотя бы одно из них отрицательное.

Пример5. ,

.

в). В подынтегральной функции степень числителя меньше на единиц степени знаменателя . Следует увеличить степень числителя, умножив его на выражение , равное единице.

Пример 6. .

Пример 7.

г). В подынтегральной функции степень числителя больше или равна степени знаменателя. В числителе заменить на или на

Пример 8.

.

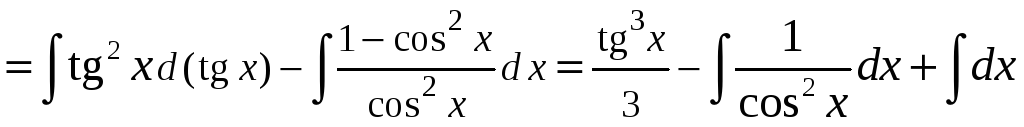
Случай 4.

, где −рациональная функция от :

а) если , то следует подынтегральное выражение выразить через и ,

б) в остальных случаях (не рассмотренных ранее) следует подынтегральное выражение выразить через и .

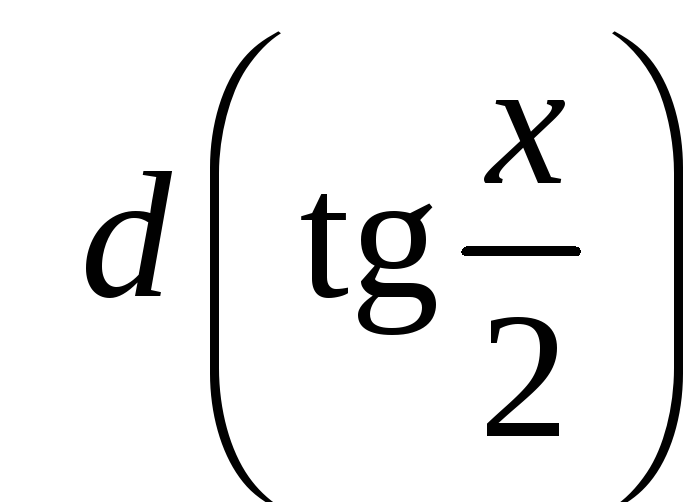Поясним эти рекомендации на примерах.

Пример 9.

Пример 10.

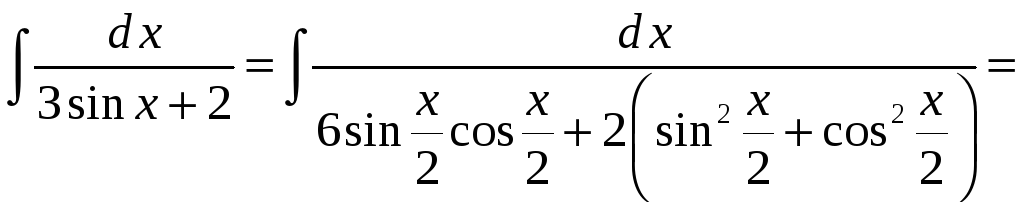
Оглавление

3. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ 1

3.1 Интегрирование тригонометрических функций 1

Оглавление 6