8. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ДВОЙНОЙ ИНТЕГРАЛ, ЕГО ПРОСТЕЙШИЕ СВОЙСТВА. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ.

8.1 Вычисление двойных интегралов базируется на понятии повторного интеграла.

Пусть рассматривается на плоской области и она правильная в направлении оси , т.е. всякая прямая, параллельная оси , пересекает границу области не более чем в двух точках. Тогда область удобно спроектировать на ось . Пусть проекция на есть .

Если – уравнение нижней границы, а – уравнение верхней границы, то любому области принадлежат те точки вертикального отрезка, которые удовлетворяют неравенствам

(*)

Выражение вида называется повторным интегралом от функции по области . Он вычисляется следующим образом:

сначала находится внутренний интеграл ( – переменная интегрирования, – фиксированная), а затем полученную функцию аргумента интегрируем на .

Значение повторного интеграла – число.

Пример 1. Вычислить повторный интеграл , восстановив область .

Решение. Интеграл вычисляется по : (см. рисунок).

.

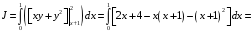
Аналогично:

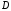если область – правильная в направлении оси , то ее удобно проектировать на ось . Пусть проекция области на ось есть отрезок , уравнение левой границы области , а правой границы – . Тогда для всякого значение точек прямой , принадлежащих области , удовлетворяет неравенствам . Поэтому область можно задать в виде

(см. рисунок).

Такому заданию области соответствует повторный интеграл . Для его вычисления находится сначала внутренний интеграл, а затем внешний. Результат – число!

Пример 2. Зададим область примера 1, проектируя ее на ось , Вычислить повторный интеграл .

Решение.

.

Замечаем, что значения различных повторных интегралов функции по области оказались равными.

Доказано (см. [1]) утверждение:

если непрерывна на , ; область является правильной в направлении осей координат, то значение двойного интеграла совпадает со значением соответствующего повторного интеграла, причем результат не зависит от порядка интегрирования, т.е.

.

8.2 Замена переменных в двойном интеграле

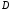Пусть на плоскости задана область , заданы функции отображающие область в область на плоскости (см. рисунок), причем точке соответствует точка , частичные прямоугольники в отображаются в криволинейные четырехугольники в плоскости .

Предположим, что преобразование является непрерывным, дифференцируемым и взаимно обратным. Тогда можно найти функции определяющие обратное преобразование области в область , которые являются также непрерывными и дифференцируемыми, если не обращается в ноль определитель Якоби (якобиан) , причем абсолютная величина якобиана задает коэффициент искажения преобразования и .

Поэтому при замене переменных с указанными свойствами в двойном интеграле следует применять формулу

.

Например, для перехода к полярным координатам якобиан , и поэтому при переходе к полярным координатам в двойном интеграле имеем

,

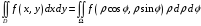здесь – образ области рассматривается в полярных координатах.

Итак, для вычисления двойного интеграла нужно задать область интегрирования неравенствами и перейти к повторному интегралу.

8.3 Типовые примеры

1) Вычисление двойных интегралов

См. примеры 1,2.

Пример 3. Вычислить двойной интеграл , где область ограничена эллипсом .

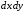Решение. Введем так называемые "обобщенные полярные координаты" Тогда уравнение эллипса запишется в виде , якобиан перехода к этим координатам и в двойном интеграле заменим на , т.е.

.

2) Площадь плоской фигуры

Пример 4. Найти площадь фигуры, ограниченной кривой .

Решение. Кривая ограничивает плоскую фигуру на плоскости , поэтому площадь фигуры можно вычислить по формуле

.

Представим на рисунке область и выберем способ счета. Поскольку переход к явному заданию границы фигуры затруднен, а кроме того, есть комбинация переменных 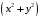, то разумно перейти к полярным координатам Получим или – уравнение лемнискаты (см. в 7.7.1 пример 7). Используя симметрию фигуры, вычисляем площадь .

Пример 5. Вычислить площадь фигуры , ограниченной кривыми , , , при .

Решение.

.

3) Объем цилиндрического тела

Пример 6. Вычислить объем цилиндрического тела, расположенного между плоскостями и и ограниченного поверхностью и плоскостью .

Решение. Тело имеет основание – область 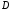на плоскости (см. рисунок), причем Цилиндрическая поверхность

с образующей, параллельной оси , и направляющей по границе образует боковую поверхность тела; сверху тело ограничено частью плоскости . Поэтому объем тела (цилиндрического тела) вычисляем следующим образом:

.

4) Механические приложения

Пример 7. Пластина имеет форму прямоугольника со сторонами длиной и . Найти массу этой пластины, если ее плотность распределения массы в произвольной точке равна квадрату расстояния от точки до одной из вершин пластины.

Решение. Введем прямоугольную систему координат так, что начало координат совпадает с вершиной, а стороны прямоугольника расположены на осях координат (см. рисунок).

Тогда , масса пластины

.

Пример 8. Найти центр тяжести пластины примера 7.

Решение. Координаты центра тяжести материальной фигуры ищем по формулам и . Значение массы пластины можно считать известным (см. пример 7). Вычислим соответствующие статистические моменты:

.

.

Поэтому ;

.

В частности, если , то центр тяжести квадрата с есть точка , где (см. рисунок).

Оглавление

8. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ДВОЙНОЙ ИНТЕГРАЛ, ЕГО ПРОСТЕЙШИЕ СВОЙСТВА. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ. 1

8.1 Вычисление двойных интегралов базируется на понятии повторного интеграла. 1

8.2 Замена переменных в двойном интеграле 5

8.3 Типовые примеры 7

1) Вычисление двойных интегралов 7

2) Площадь плоской фигуры 8

3) Объем цилиндрического тела 10

4) Механические приложения 11