2. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ.

2.1 Метод подведения под знак дифференциала

Этот метод применяется для вычисления интегралов вида . Воспользуемся тем, что . При этом говорят, что мы подвели функцию под знак дифференциала. Если еще сделать замену , то мы получим интеграл более простой, чем первоначальный:

.

После нахождения этого интеграла следует вернуться к переменной , заменив на .

Отметим, что при подведении функции под знак дифференциала прежде всего используется определение дифференциала и два его свойства

,

.

Рассмотрим, как подвести под знак дифференциала некоторые функции:

, ,

, ,

, ,

, .

Список таких формул можно продолжить. Важно понять, как они получаются.

Рассмотрим примеры на вычисление неопределенных интегралов методом подведения под знак дифференциала.

Пример 1.

.

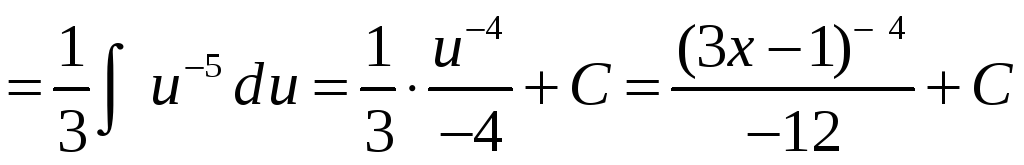Мы использовали свойства дифференциалов .

Пример 2. Найти интеграл .

Воспользуемся правилом подведения под знак дифференциала

и введем новую переменную . Тогда

В дальнейшем, когда появится навык, можно вводить новую переменную только "мысленно".

2.2 Метод замены переменной

Во многих случаях введение новой переменной интегрирования позволяет свести данный интеграл к более простому. Такой метод называется методом замены переменной или методом подстановки.

Пусть функция непрерывно дифференцируема на промежутке и имеет обратную функцию . Тогда

.

При замене переменной в интеграле нужно

а) заменить переменную на функцию , заменить на ,

б) вычислить получившийся интеграл,

в) результат выразить через первоначальную переменную .

Пример 1. Найти . Это − интеграл типа .

В соответствии с рекомендацией сделаем замену . Тогда , Подставим выражения для в интеграл:

.

Получившийся результат надо выразить через переменную . Учитывая, что получим

.

Пример 2. Найти . Это − интеграл типа .

В соответствии с рекомендацией сделаем замену . Тогда

.

Подставляя выражения для в интеграл, получим

Получившийся результат надо выразить через переменную , учитывая, что . Удобно воспользоваться прямоугольным треугольником с углом t, противолежащим катетом и прилежащим катетом, равным 3 (рис. 38). Тогда

и .

Пример 3. Найти .

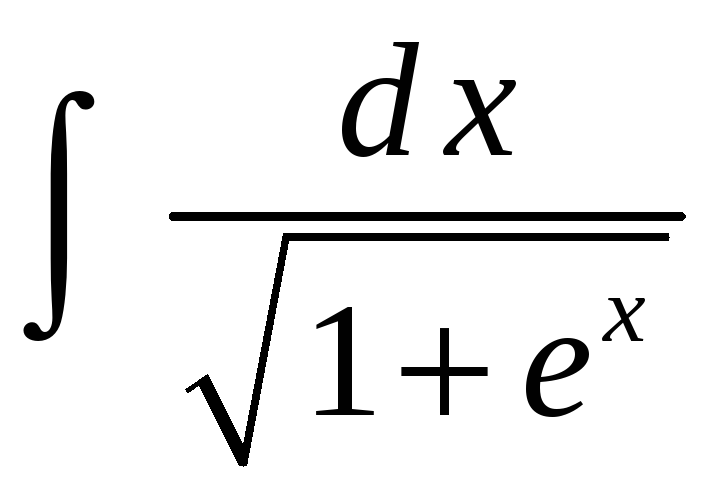Сделаем замену переменной Тогда ,

.

Подставляя , получим .

2.2Метод интегрирования по частям

Пусть и – дифференцируемые функции. Найдем дифференциал их произведения: . Проинтегрируем это равенство и воспользуемся свойством . Тогда получим формулу или

.

Эта формула называется формулой интегрирования по частям. Формула применяется, когда подынтегральное выражение можно представить в виде произведения двух множителей и так, чтобы отыскание функции по ее дифференциалу и вычисление интеграла составляли в совокупности задачу более простую, чем вычисление интеграла .

Умение разбивать разумным образом подынтегральное выражение на множители и вырабатывается в процессе решения задач. Укажем, когда и как это делается в некоторых случаях:

1) интегралы ,

где – многочлен, вычисляются многократным интегрированием по частям, причем следует взять , а оставшееся выражение взять за ;

при каждом применении формулы степень многочлена будет понижаться на единицу;

2) интегралы вида также вычисляются методом интегрирования по частям, но за следует взять соответственно функции .

Пример 1. Найти интеграл .

Положим . Тогда , .

При отыскании функции мы взяли постоянную интегрирования . Легко проверить, что это не повлияет на конечный результат. Теперь применим формулу:

.

Еще раз применим формулу интегрирования по частям, положив . Тогда ,

.

Заметим, что если в первоначальном интеграле положить , то формула приведет к интегралу , более сложному, чем первоначальный.

Пример 2. Найти .

Положим . Тогда и, используя формулу, получим

.

Преобразуем подынтегральную функцию: . Тогда

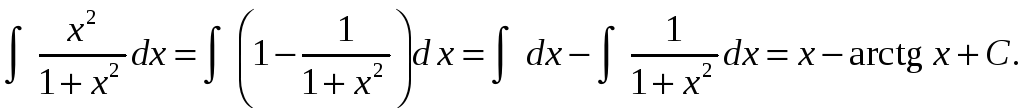
Итак, окончательно, .

Пример 3. Найти интеграл .

Положим 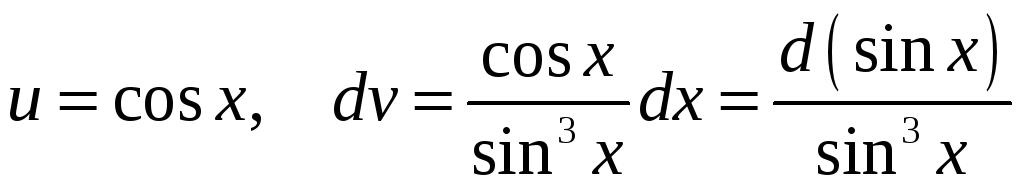. Здесь такой выбор и менее очевиден, чем в предыдущих примерах. В выражение для мы включили , чтобы получить и легко вычислить v: . Тогда

.

Пример 4. Найти интеграл .

Положим Тогда ,

.

Еще раз применим метод интегрирования по частям, положив . Тогда ,

.

Подставляя полученное значение интеграла в равенство , получим:

или и .

Здесь мы получили одну из первообразных. Чтобы записать множество первообразных, нужно добавить произвольное число . Итак,

.

Мы рассмотрели основные методы интегрирования – метод подведения под знак дифференциала, метод интегрирования по частям, метод замены переменной. Но эти методы далеко не всегда облегчают отыскание интеграла. Далее мы рассмотрим некоторые классы функций, для интегрирования которых есть свои специальные приемы.

2. ЛЕКЦИОННОЕ ЗАНЯТИЕ. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ. 1

2.1 Метод подведения под знак дифференциала 1

2.2 Метод замены переменной 2

2.2Метод интегрирования по частям 4