
FIZIKA_OTVETY
.pdf
это
D) равен нулю, если токи не пересекают поверхность.
34)НТ-1. Элементарный поток вектора магнитной индукции через площадку |
||||||
|
|
|
|
|
|
|
|
|
|
|
h |
||
|
|
|
|
|
B |
|
|
|
|
|
|||
|
|
|
|
|
||
А) |
B dS .*В) B ndS . |
|
|
|||
|
|
|
|
|
|
dS |
С) |
Bxn dS .D) nxB dS |
|
|
|||
dS
(рис.)
35)НТ-1 Опыт показывает, что поток вектора B через любую замкнутую поверхность
всегда равен нулю. Физическая причина этого обстоятельства А) силовые линии магнитного поля – всегда окружности
*В) В природе не обнаружено магнитных зарядов, все наблюдаемые магнитные поля возникают в результате протекания некоторых электрических токов.
С) Магнитное взаимодействие является дополнительным к электрическому для движущихся электрических зарядов.
D) Работа магнитной составляющей силы Лоренца, действующей на электрические заряды всегда равна нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36)НТ-1. Поток вектора магнитной индукции |
B через замкнутую поверхность равен |
||||||||||||||
|
Bn dS = 0 I K . |
|
|
|
|
|
|
|
|
|
|||||
А) |
|
|
|
В) BdS |
= 0 jK . |
||||||||||
|
S |
|
|
K |
|
|
|
|
S |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(B n)dS 0 . D) |
|
|
|
|
|
|
|
K |
|
||||
*С) |
BdS = |
|
|
q . |
|||||||||||
|
|
|
|
||||||||||||
|
S |
|
|
|
S |
|
|
|
|
K |
|
|
|
||
|
I |
|
|
|
|
|
|
|
|
|
|
|
|||
где |
K |
– токи текущие по поверхности, |
j |
K |
– вектора плотности токов вытекающих из |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
объема ограниченного поверхностью, |
q |
K |
– электрические заряды, расположенные на |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности.
37)НТ-1. Известно, что одно из интегральных уравнений Максвелла для магнитного поля |
|||||
имеет вид |
|
|
|
. Уравнение справедливо |
|
B dS |
= 0 |
||||
|
|
||||
|
(S ) |
|
|
|
|
А) Только для стационарных полей В) Только в вакууме и однородных магнетиках.
*С) Для любых полей и известных природных условий.
D) Если силовые линии магнитной индукции замкнуты (не уходят в бесконечность). 38)НТ-1. Известно, что одно из интегральных уравнений Максвелла для магнитного поля
имеет вид |
|
|
, где |
S |
– некоторая замкнутая поверхность. В уравнении |
||||
BdS = 0 |
|||||||||
|
|
|
|
|
|
|
|||
|
|
(S ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n – нормаль к элементу поверхности |
|||
А) |
BdS |
– векторное произведение, dS = ndS , |
|||||||
dS . |
|
|
|
|
|
|
– нормаль к dS , |
||
В) BdS |
– скалярное произведение dS = ndS , n |
|||
вектора магнитной индукции внутри объема, ограниченного S . |
||||
|
|
|
|
– нормаль к dS |
*С) BdS |
– скалярное произведение dS = ndS , n |
|||
вектора магнитной индукции на каждом элементе dS поверхности S .
B
,B
– значения
значение

39)НТ-1. Интегральное уравнение Максвелла
Bn dS = 0 S
утверждает
*А) Потоки вектора магнитной индукции любого электромагнитного поля через
произвольные замкнутые поверхности равны нулю. |
|
||||
|
|
|
|
|
|
В) Источники (и стоки) магнитной индукции |
B |
всегда находятся за пределами |
|||
ограниченной замкнутой поверхности. |
|
|
|||
С) Т.к. магнитное поле является вихревым, то все силовые линии поля возникающие |
|||||
внутри поверхности S ее не пересекают. |
|
|
|||
|
|
|
|
|
|
D) Циркуляция вектора B по замкнутому контуру равна нулю |
|||||
|
|
|
|
|
|
41)НТ-1. Теорема Гаусса для магнитного поля |
B |
утверждает |
|||
А) |
|
|
. |
|
|
Bd = 0 |
|
|
|||
|
|
|
|
||
|
|
|
|
|
В) |
|
|
|
|
BdS = 0 I i |
||||
|
S |
|
|
i |
*С) |
|
. |
||
|
BdS = 0 |
|||
|
|
|
||
.
|
S |
D) |
|
Bd |
|
|
|
|
|
|
Ii |
= 0 |
|
|
i |
.
Где S – замкнутая поверхность, токов, пересекающих поверхность.
– замкнутый контур на поверхности
I |
i |
|
– один из
ток
42)НТ-2. Магнитное поле
I в точке М равно |
|
|
*А) 0 В) |
0 I |
.С) |
2 r |
||
|
|
|
|
|
|
|
|
|
|
|
|
B , создаваемое отрезком проводника |
|||||||||||
|
|
0 |
I |
|
. D) |
|
0 |
I |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
2 (r + ) |
I |
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
2 |
|
+ |
|
|
|
|
|
|
|||
r |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
, по которому течет
r M
I
43)НТ-3. Магнитное поле рис., по которому течет ток I
А) |
|
0 |
I |
1 |
+ |
1 |
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
r |
|
r + |
|
|
|
|||||
С) |
|
0 |
I |
1 |
+ |
1 |
+ |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2r |
r |
|
r + |
|
|||||
B , создаваемое в точке
,равно
*В) |
|
0 |
I |
1 |
− |
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
4 |
r |
|
r + |
|||
D) |
|
0 |
I |
1 |
+ |
1 |
− |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
2 |
2r |
r |
r + |
|||||
|
|
|
|
||||||
M
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
проводником, изображенным на
|
|
|
|
|
r |
|
|
M |
|
I |
I |
. |
|
→ |
|
|

M
|
|
44)НТ-1. Магнитное поле |
B , создаваемое в точке |
проводником, изображенным на рис., по которому
 r
r 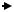
M
течет ток I |
направлено |
|
|
|
|
|
|
I |
I |
||||
|
|
|
|
|
|
|
|
|
|
|
→ |
||
А) |
от нас |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
В) Направо →. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
*С) к нам |
|
|
|
|
|
|
|
|
|
|
|
|
|
D) направление зависит от длины участка |
( ) |
проводника. |
|
|
|
||||||||
45)НТ-2. В бесконечно длинном проводнике радиуса - "a" при постоянной плотности |
|||||||||||||
тока в сечении зависимость магнитной индукции |
B |
от r |
– расстояния до оси симметрии |
||||||||||
проводника имеет вид |
B |
|
|
|
|
|
|
|
|
|
|||
А) B |
|
В) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r |
|
|
r |
|
|
|
|
|
|
||
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B
С)
a
r
B
*D)
a
r
46)НТ-1. Закон полного тока |
|||
|
|
|
|
А) поток вектора |
B |
или |
H |
|
|
|
|
С) циркуляцию вектора |
E . |
определяет в конкретных условиях |
|
|
|
|
|
|
|
|
|
. |
*В) циркуляцию вектора |
B |
или |
|
|
|
|
|
|
|
D) дивергенцию вектора |
B . |
||
H
.
47)НТ-1. Закон полного тока в вакууме имеет вид
|
|
|
|
|
||
*А) |
Bd |
|||||
|
|
|||||
|
|
|
|
|
||
|
|
|
||||
D) |
Bxd |
|||||
|
||||||
= =
0 Ii i
0 Ii i
.
|
|
|
|
0 |
|
|
i |
|
|
В) |
Ed = |
I |
. |
||||||
|
|
|
|
||||||
i
.Где |
|
– замкнутый контур, |
|
|
|
|
0 |
|
|
i |
|
|
|
|
||||
|
С) |
|
BdS = |
|
|
I |
. |
|
|
S |
|
|
i |
|
|
S |
– замкнутая поверхность |
||||||
I |
i |
– электрические токи. |
|
|
|
48)НТ-1. Закон полного тока для квазистационарного магнитного поля в вакууме имеет |
||
|
|
|
вид Bd = 0 Ii . В правой части уравнения стоит
i
А) Арифметическая сумма токов, текущих сквозь замкнутую поверхность стягиваемую замкнутым контуром .
В) Алгебраическая сумма токов текущих по поверхности, ограниченной контуром .
*С) Алгебраическая сумма токов пересекающих любую поверхность, стягиваемую замкнутым контуром .

|
49)НТ-1. Закон полного тока для квазистационарного магнитного поля в вакууме имеет |
|||||||
вид |
|
|
. В левой части уравнения стоит интеграл |
|
|
|
|
|
Bd = 0 Ii |
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||
|
А) по замкнутой поверхности от скалярного произведения |
|
||||||
|
B |
и d = e d где |
||||||
– единичный вектор, касательный к d – элементу площади . |
|
|
|
|||||
e |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
В) по замкнутому контуру от векторного произведения |
B на |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
d = e d направленный элемент длины контура |
|
|
|
|
|
|||
|
*С) по замкнутому контуру от скалярного произведения |
B на d – направленный |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d . |
|
элемент длины контура |
. Значение B( ) берется непосредственно на элементе |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B на |
d |
значение |
||
|
D) по замкнутому контуру от скалярного произведения |
B берется |
||||||
в центре площадки, стягиваемой контуром |
. |
50)НТ-2.
|
|
А) lim |
(S |
|
|
V →0 |
|
|
|
|
|
|
|
Дивергенция вектора B(divB |
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
BxdS |
|
BdS |
|||
|
|
|
|
||
) |
. |
*В) lim |
(S ) |
|
|
V |
|
V |
|
||
|
S →0 |
|
|
||
|
|
|
|
|
|
|
|
|
= B) равна |
||
|
|
|
. |
BdS |
|
С) |
|
|
|
S |
|
|
V |
|
.
D)
|
|
lim BdS |
|
S →0 |
|
S |
|
.
|
|
51)НТ-2. Дифференциальную операцию над вектором |
B(r , t ), значение которой |
доказывает, что в окружающем нас мире отсутствуют «магнитные» заряды записывают в виде |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А) |
rotB |
= xB . |
|
|
|
|
|
|
|
|
|
|
|
|
В) gradB = B . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
*С) divB = B . |
|
|
|
|
|
|
|
|
|
|
|
D) divrotB |
= xB . |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52)НТ-2. Дифференциальная операция над вектором |
B |
, которую называют |
|
||||||||||||||||||||||||||||||||||||||
дивергенцией, в прямоугольной системе координат равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
By |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
B |
x |
|
|
|
|
|
B |
|
|
|
|
B |
|
B |
|
|
B |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
*А) divB(x, y, z) |
= |
|
|
|
|
+ |
|
|
|
+ |
|
z . В) divB |
= |
|
|
+ |
|
|
+ |
|
|
. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
y |
z |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
2 |
B |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||
|
|
B |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
B |
|
|
B |
|
|
B |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С) |
|
|
|
|
x |
+ |
|
|
|
|
|
y |
+ |
|
|
|
|
|
z |
. |
|
|
|
|
D) |
|
|
|
+ |
|
|
|
+ |
|
|
|
|
. |
|
|
|
x |
2 |
|
|
y |
2 |
|
z |
2 |
|
|
|
|
|
x |
2 |
y |
2 |
z |
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
53)НТ-2. Закон полного тока в дифференциальной форме имеет вид |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
*А) rotH = |
|
j |
. |
|
В) divH |
= |
j . |
С) graddivH |
= |
j . |
|
D ) rotrotH = |
j . |
||||||||||||||||||||||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
54)НТ-3. Ротор вектора |
B(rotB |
= xB), который также является вектором, имеет |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bd |
|
|
|
|
|
|
|
|
|
, yz – контур |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S yz = y z |
|
|||||||||||||||||
проекцию на ось х, равную |
|
*А) rot B = |
|
lim |
yz |
|
|
, где |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
S yz →0 |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BxdS |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
rot B = lim |
|
|
Bd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|||||||||||||||
охватывающий |
|
S |
|
|
.В) |
|
|
. |
|
|
|
|
С) rot B = lim |
|
|
|
|
|
, где |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
yz |
|
|
|
|
|
S |
|
|
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
V →0 |
|
|
|
V |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
` y z |
|
|
|
|
|
|||||||||||
BxdS – векторное произведение Bxn |
|
|
|
n |
– нормаль к поверхности |
; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dS = dydz . |
|
|
|
|
|
|
|
|
D) rot |
|
B = lim |
|
|
|
BxdS . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55)НТ-1. Вспомогательный вектор |
|
H |
|
|
(напряженность магнитного поля), используемый |
|||||||||||||||||||||||||||||||||||||||||||||
для количественного описания магнитных полей, связан в вакууме с вектором магнитной |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
индукции соотношением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
||||||||||||
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
А) B = |
|
|
. В) H = 0 |
0 B . |
|
|
|
|
*С) H = |
. |
|
|
|
|
|
D) H = |
|
|
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
56)НТ-1. Дифференциальные уравнения Максвелла для квазистационарного магнитного |
||||||||||||||||||||||||||||||||||||||||||||||||||
поля имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
rotH |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
А) divB |
= |
0 |
j , |
|
|
|
|
|
|
|
|
В) rotH |
= |
j |
, |
divB |
= q . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
= |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
*С) divB |
, |
rotH |
= |
j . |
|
|
|
|
D) |
graddivH = |
j |
, |
divB |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
57)Н-2. Дифференциальное уравнение Максвелла для квазистационарного поля имеет |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вид rotH = |
|
j |
. Дифференциальная операция |
rotH |
= xH |
|
есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
*А) вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
В) скалярная дифференциальная операция первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
С) скалярная дифференциальная операция второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
D) вектор, в прямоугольной системе координат равный |
|
|
|
H |
x |
|
H |
y |
|
H |
z |
. |
||||||||||||||||||||||||||||||||||||||
|
e |
|
|
|
+ e |
|
|
|
|
+ e |
|
|
|||||||||||||||||||||||||||||||||||||||
|
x |
x |
|
y |
|
y |
|
z |
z |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

58)НТ-2. Проекции вектора магнитной индукции, создаваемой током, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y = 0 с линейной плотностью тока |
|
|
|
|
|
|
||||||||||||||||||||
бесконечной плоскости |
j = − je |
z |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) Bx |
|
= 0; y 0 |
Bz = − |
|
0 |
j |
y 0 |
Bz |
= |
|
0 |
j ; By = 0 . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
В) Bx |
|
= 0, Bz = 0 |
y 0 |
|
By |
= |
|
0 j |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*С) B |
|
= 0 |
; B |
|
= 0 |
; |
y 0 |
|
|
|
|
0 j ; |
y |
0 |
B |
|
= − |
|
0 |
j |
. |
|
||||||||||||
y |
z |
B |
x |
= |
x |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
D) B |
|
|
= 0 |
; B |
|
|
= 0 ; |
y 0 |
|
B |
|
= |
|
j ; |
y 0 |
B |
= − |
|
x |
|
|
|
||||||||||||
y |
z |
|
x |
0 |
0 |
j . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||
текущем по
(рис.) равны
z
j
 y
y
59)НТ-2. Проекции бесконечной плоскости
вектора магнитной индукции, создаваемой |
||
|
|
|
y = 0 с линейной плотностью тока |
j |
= |
током, |
|
|
|
− je |
x |
|
|
текущем по
(рис.) равны
|
|
А) |
Bx |
|
|
= 0 |
; By = 0 ; |
y 0 |
Bz |
= |
|
0 |
|
j |
; Bz |
= − |
|
0 |
j |
. |
|
z |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
*В) B |
x |
|
= 0 |
; B |
y |
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y 0 |
B |
|
|
|
= − |
|
0 |
j |
; y 0 |
B |
|
= |
|
0 |
j |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
z |
|
|
|
|
|
2 |
|
|
|
|
|
z |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
x |
= 0 |
; B |
y |
= 0 ; |
y 0 |
B |
z |
= − |
0 |
j |
; y |
|
0 |
B |
= |
|
0 |
j . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
||||||||
|
|
D) Bx = 0; By = 0 j ; y 0 |
Bz |
|
= − |
0 j |
; y 0 Bz = 0 j . |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
21.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60)НТ-1. Модуль и направление магнитного дипольного момента |
P |
плоского |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
проводящего контура с током вдоль контура |
I , равны |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, где S – любая площадь стягиваемая контуром, |
|
|
|
|
||||||||||||||||||||||||
|
|
А) |
PM |
|
|
|
= SIn |
|
n – нормаль к э той |
|||||||||||||||||||||||||||||||
поверхности в центре симметрии контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
*В) P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||
|
|
|
|
= SIn |
, где |
– площадь участка плоскости, охватываемого контуром, |
– |
|||||||||||||||||||||||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на поверхности S . |
|
|
|
|||||
нормаль к плоскости, совпадающая по направлению с B |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, где S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
С) |
PM |
|
|
= SB |
|
– площадь участка плоскости, охватываемого контуром B – |
|
|||||||||||||||||||||||||||||||
магнитная индукция, создаваемая током |
|
I |
|
|
в центре симметрии контура на плоскости. |
|
|
|||||||||||||||||||||||||||||||||

61)НТ-2. Проекции вектора магнитной индукции, создаваемый |
|
|
|
«бесконечной» плотности z = 0 , с линейной плотностью тока |
j |
током, |
||
= |
|
|
je |
x |
|
|
|
|
текущим вдоль
(рис.) равны
А)
B |
z |
|
=
0
;
B |
x |
|
=
0
;
x
z 0 |
By = |
|
0 j |
|
; z 0 By = − 0 j . |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
В) |
B |
|
|
= |
|
0 |
j |
; B |
|
|
= 0; B |
|
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
z |
|
|
|
2 |
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С) |
B |
z |
= 0 ; |
z 0 |
B |
x |
= |
0 j ; |
z |
0 z 0 |
B |
x |
= − |
0 j . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
*D) B |
|
= 0 ; B |
|
|
= 0; z 0 |
|
|
|
|
|
|
0 j |
; |
B |
|
|
= |
|
0 |
j |
. |
||||||||||||||||||
z |
x |
B |
y |
= − |
y |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||||||||
62)НТ-2. График зависимости |
y -компоненты магнитной индукции в |
||||||||||||||||||||||||||||||||||||||
вакууме, создаваемый током, текущим вдоль «бесконечной» плоскости |
|||||||||||||||||||||||||||||||||||||||
z = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||
с линейной плотностью тока j |
|
je |
x |
(рис.) имеет вид |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) |
|
|
By |
|
|
|
|
|
|
|
|
j |
|
|
В) By |
|
|
|
|
0 j |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
z |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С) |
|
|
|
|
By |
|
|
|
|
|
|
|
0 j |
*D) |
|
By |
|
|
|
|
|
|
|
|
0 |
|
j |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j
 z
z
x
j
z
63)НТ-1. Проекции вектора магнитной индукции, создаваемый |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«бесконечной» плотности |
z = 0 |
, с линейной плотностью тока |
j |
||||||||||||||||||||
*А) |
|
|
|
|
B |
y |
|
|
|
В) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
j |
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С) |
|
|
|
|
|
|
|
|
|
|
2 |
D) |
B |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
B |
|
|
|
|
|
|
|
|
j |
y |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
током, |
||
= |
|
|
je |
x |
|
|
|
|
y
текущим вдоль
(рис.) равны
x
j
z

|
|
64)НТ-1. Магнитное поле |
(B) внутри бесконечно длинного соленоида (катушки) равно |
||||||||||||||||||||||||||
|
|
*А) |
0 |
I |
n |
n , где |
I |
n |
– ток текущий по виткам в соленоиде; n – число витков |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
приходящихся на единицу длины соленоида. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
В) |
In |
|
|
где I |
– ток по проводу из которого состоят катушка, n – число витков, |
|
|
|
|||||||||||||||||||
приходящихся на единицу длины соленоида. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
С) |
|
0 |
I |
|
, где |
I – ток по проводу из которого состоит катушка n . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D) |
|
0 |
|
I |
n |
S |
, где |
I |
– ток по проводу из которого состоят катушка, |
n – число витков, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
приходящихся на единицу длины соленоида, S – площадь поперечного сечения катушки |
|
||||||||||||||||||||||||||||
соленоида. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67)НТ-2 Момент (M ) сил Ампера, действующих на магнитный дипольный момент |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
|
в магнитном поле |
B |
равен |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
А) |
P |
B . |
|
|
В) |
P |
B = P B cos . |
*С) |
PxB , |
|
M = P B sin . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
D) |
BPm . |
|
|
|
– угол между векторами |
Pm и B . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68)НТ-1 Механический момент M сил Ампера действующих на магнитный дипольный |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момент |
p |
m |
|
в магнитном поле |
B направлен |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
А) вдоль |
|
p |
m |
. |
В) вдоль |
B . |
С) лежит в плоскости векторов p |
m |
и |
B |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и перпендикулярен B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
*D) Перпендикулярен |
p |
m |
и B , и определяется правилами векторного произведения |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p |
m |
B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69)НТ-1. Вектора |
pm – магнитного момента и B |
расположены в плоскости рис. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M )сил Ампера, действующий на |
|
|
|
|
|
|
|
|
||||||||
Механический момент |
p |
m |
направлен |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*А) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
С)
B
pm
M
D)
 B
B
pm
M

70)НТ-2. Прямоугольная рамка с током |
I |
|
(рис.) помещена в однородное магнитное |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поле B |
. n – нормаль перпендикулярная плоскости, в которой расположена рамка. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекция на n момента сил (M ) |
действующего на рамку равна |
|
|
|
|
|||||||||||
|
|
B |
|
|||||||||||||
А) |
abIB . |
В) − abIB . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
n |
|
|
*С) 0. |
D) |
bIB . |
|
|
|
|
a |
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
71)НТ-2. Прямоугольная рамка с током |
|
находится в магнитном поле (рис.). |
n |
– |
||||||||||||
единичный вектор нормали к плоскости рамки. Значение момента сил Ампера и его |
|
|
||||||||||||||
направление равны |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А) |
M = abIBcos |
, M = Mex . |
|
|
|
|
h |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В) |
M = abBI sin , M = Mex . |
|
|
I |
|
|
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
*С) M = abBI sin , |
M = −Me . |
I |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
b |
|
|
|
|
|
|||
|
M = abIBsin |
|
|
|
|
|
|
|
|
|
||||||
D) |
, M |
= Me |
y |
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74)НТ-2. Прямоугольная рамка с током |
I (I = const) ( (рис.) находится в |
|
|
однородном магнитном поле
А) IabB cos .
*С) − IabB cos
B .Механическая потенциальная энергия в B равна
В) IabBsin . |
z |
|
|
||
|
|
|
|
|
|
.D) − |
I |
ab cos . |
|
h |
|
2 |
|
|
B |
||
|
|
I |
|
|
|
|
|
|
|
|
|
|
I |
a |
|
|
|
x |
|
b |
y

|
75)НТ-3. Отрезок проводника |
, в котором ток |
I |
|
|||
поддерживается постоянным, под действием силы Ампера |
|
||||||
|
|
|
|
|
|
|
|
перемещается в пространстве на вектор перемещения |
r . |
S |
|||||
– площадка, построенная на отрезках и r , |
– |
|
|||||
магнитный поток через площадку. Работа силы Ампера по |
|
||||||
перемещению проводника равна |
|
|
|
||||
|
*А) |
I . |
В) − I . |
|
|
|
|
|
I |
2 |
|
I |
|
|
|
|
|
|
|
|
|
|
|
С) |
2 |
. |
D) |
2 |
. |
|
|
|
|
|
|
|
|
||
A
B
|
|
|
|
h |
|
I |
I |
|
|
|
|
r |
S |
|
76)НТ-3. При постоянном токе в замкнутом контуре работа силы Ампера при его |
|
|||||||||||||||||||||||||||||
перемещении в постоянном магнитном поле всегда равна |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ( |
|
|
− ) |
|
( |
|
− ) |
|
|||||
|
A12 = I ( 2 − 1 ) |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||
*А) |
|
|
|
|
|
|
|
|
|
|
|
|
|
В) |
A |
= |
|
2 |
|
|
1 |
|
С) |
|
2 |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2I |
|
|
|
|
|
( |
|
− )I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 и |
1 |
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
D) |
|
|
2 |
|
|
1 |
|
|
.Где |
потоки |
|
, пронизывающие контур в конечном |
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) и начальном (1) положении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77)НТ-3. Потоки вектора |
B |
|
в стационарном магнитном поле пронизывающие |
|
||||||||||||||||||||||||||
замкнутый электрический контур с неизменным током |
|
I |
в его конечном и начальном |
|
||||||||||||||||||||||||||
положении равны |
2 |
и |
1 . Работа силы Ампера при перемещении контура описывается |
|||||||||||||||||||||||||||
соотношением |
A |
|
= |
…. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
A |
|
= I ( |
2 |
− |
1 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
78)НТ-1. Гиромагнитное отношение это отношение |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А) энергии магнитного дипольного момента системы в |
B |
к ее энергии вращательного |
||||||||||||||||||||||||||||
движения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*В) магнитного момента системы к его механическому моменту импульса. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С) силы Лоренца, действующей на заряды в |
B , к центростремительному ускорению |
|||||||||||||||||||||||||||||
при их вращении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D) момента силы Лоренца к моменту импульса частиц при из вращении в |
B . |
