FIZIKA_OTVETY

уд а ле н и я д иэ ле к тр ик а с д иэ л ек тр ич ес ко й пр о н и цае м о с ть ю ε и за по л н я юще го все пр о с тр а нс т во м е ж д у о б к ла д кам и р ав н а

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

Эн ер г и я ко нд е нса то р а по с л е уд а ле н и я д иэ л е к тр и ка

_ _ _ _ _ _ _ _ _ _ _ _

С – ем ко с ть ко н де нса т о р а по с ле уд а ле н и я д иэ ле к тр и ка .

Пр а ви л ь ны й о т ве т : D

Н . Т . 3 1 8 1 . Ко н де нса т о р ем ко ст ью С , м е ж д у п ла ст и на м и

ко то р о го н а хо д и тс я д и эле к тр и к , з ар я ж ен до н апр я же н и я U 0 . Не о т к люч ая ко н де н са т о р о т ис то ч н и ка , из ко н де нс ато р а

уд а л яю т д иэ ле к тр и к . П р и э то м со в ер ша ет ся р або та

_ _ _ _ _ _ _ _ _ _ _ _ _ , а э нер ги я ко н де нс ато р а _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

С – ем ко с ть ко н де нса т о р а б ез д иэ ле к тр ик а

Пр а ви л ь ны й о т ве т : A

83

Н . Т . 2 1 8 2 . О б ъем на я п ло т но с ть э н ер г и и

В ыбер и те др уг и е пр а в и ль н ые выр а ж е ни я

Пр а ви л ь ны й о т ве т : A , B

84

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Тест: Физика - 2 сем. (демо-версия). 60 мин. (Кол-во вопросов: 28) Стоячая электромагнитная

волна образуется в результате отражения от проводящей поверхности B в точке M. На поверхности образуется:

На пути пучка стоит экран с круглым отверстием, который вырезает 7 зон Френеля для точки наблюдения М. Если закрыть 2 – 7 зоны, интенсивность света в точке М:

Атомы водорода облучаются электронами с энергией εω = 12,4 эВ. Будет ли при этом наблюдаться излучение из атомов на частотах серии Бальмера (k = 2), где k – квантовое число, определяющее энергию состояния, в которое релаксируют электроны в этой серии?

Внешний фотоэффект - это:

Апериодический режим релаксации реальных осцилляторов имеет место, только если

Если оператор физической величины, то ее среднее значение (< f >) в состоянии с волновой функцией равно

В заданном элементе пространства (рис.) значение вектора Пойнтинга в плоской гармонической волне :

Распределение интенсивности излучения на приемном экране после прохождения плоской волны сквозь дифракционную решетку описывают формулой

Правильными выражениями являются:

Неправильными выражениями являются:

Правильным соответствием между названиями волн их аналитическими выражениями будет:

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Начальная фаза результирующего гармонического колебания, полученного от сложения

Частота спектральной линии излучения из атома водорода для перехода, определяемого термами равна:

Оператор квадрата радиальной компоненты импульса электрона равен 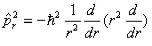; его волновая функция в основном состоянии в атоме водорода

. Среднее значение кинетической энергии электрона <εk>=..

Зависимость интенсивности линейно поляризованной волны, прошедшей через поляризатор от угла поворота α, отсчитанного от направления, при котором равна:

На рис изображен мгновенный снимок амплитуды смещения частиц в продольной упругой волне бегущей налево. В точках частицы смещаются

Зависимость магнитной индукции от координат и времени имеет вид . Плотность тока смещения в вакууме равна

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Волновое «сопротивление» диэлектрической среды для электромагнитных волн равно:

Колебательный режим в пружинном маятнике имеет место, если

Формула для зависимости амплитуды электрического заряда в конденсаторе от частоты

Спектры излучения возбужденных атомов являются:

Импульс переносимый фотоном, которому соответствует длина волны – λ,равен рν =

Уравнение волны имеет вид ,Фазовая скорость волны равна (м/c)

Интенсивность электромагнитной волны в вакууме - это среднее значение:

Если поле , то имеет компоненты:

Оператор физической величины f - это некоторое математическое преобразование волновой функции микрообъекта, которое из ψ позволяет:

Известно, что с помощью экрана с отверстием поперечного размера “d” из плоской волны можно сформировать пучок (луч), волновой пакет в направлении, перпендикулярном распространению волны. Соотношение неопределенностей для волн дает следующую оценку угловой расходимости луча:

В кристаллах длины упругих волн изменяются:

Если состояние микросистемы стационарно, то

На рисунках приведены осциллограммы ЭДС источника вынужденных колебаний RLC контура, тока и мощности тока (N(t)). Графику для ε(t) и I(t) – 1 соответствует осциллограмма (N(t))…

Волновая функция де Бройля

На рисунке приведена векторная диаграмма затухающих колебаний в электрическом контуре с циклической частотой ω в момент времени t = τ. Длина векторов 1,2,3 определяет в этот момент:

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Выберите неверные ответы. Дифракция – это:

На рис. Представлена зависимость энергии затухающих колебаний от времени. Кривая 1 описывается функцией и определяет изменение:

Период дифракционной решетки увеличили в три раза. Угловая дисперсия решетки в спектре третьего порядка:

Компоненты поля электромагнитной волны имеют вид и

. Представьте поле в виде суперпозиции линейно поляризованной

волны, определив ее амплитуду( ), угол (α) поляризации по отношению к оси Х, и характер поляризации, а также амплитуду оставшейся части поля.

Дифракция электронов имеет место, потому что

Некоторую микрочастицу , массой m, «поместили» в замкнутый куб со сторонами а, b, c

стремясь сохранить её в состоянии покоя. Минимальная её кинетическая энергия в этом случае будет порядка:

Для измерения энергии микрочастиц в монохроматичном потоке, его можно “направить” в тормозящее однородное электрическое поле (рис) плоского конденсатора.При уменьшении расстояния между плоскостями в 2 раза квантовомеханическая неопределенность измеренных значений энергии

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Если волновой пакет в отсутствие дисперсии локализован в направлении распространения в

с центральной длиной волны 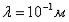, то длины электромагнитных волн, образующих волновой пакет, в соответствии с соотношениями неопределенностей должны лежать в интервале…

Добротность осциллятора, в котором амплитуда колебаний уменьшается в e раз через 100 периодов, равна:

Амплитуда затухающих колебаний изменяется со временем по закону

Микрочастицы находятся в состоянии «одномерного» движения в пространстве, в котором для них имеется «бесконечно» высокий потенциальный барьер. Квадрат модуля волновой

функции микрочастиц |ψ(x)|2 имеет вид:

Дифференциальное уравнение для функции 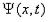вида является кинематическим для стационарной плоской волны если

Спектральный терм в атомах определяет:

Наименьшее расстояние между точками, в которых колебание электромагнитного поля в вакууме осуществляется в фазе, равно:

Здесь ν – частота колебаний

Одно из уравнений Максвелла имеет вид . Решив уравнение можно найти:

Обобщенное уравнение свободных затухающих колебаний в линейных осцилляторах имеет вид: В электрическом контуре ω0 равна:

Дифференциальным уравнением, не описывающим установившиеся вынужденные колебания, является:

Число открытых зон Френеля на круглом отверстии радиуса r0 в экране для точки

наблюдения сигнала, находящейся на расстоянии на перпендикуляре, восстановленном из центра отверстия, равно:

Электрон двигается в положительном направлении в одномерном потенциальном поле (рис.)

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

В открытой с двух концов трубе длиной L образовалась стоячая волна, соответствующая основному тону. Плотность потенциальной энергии принимает наибольшее значение в точках (точке):

Известно, что в полупроводниках наблюдают как “внешний” так и “внутренний” фотоэффект. Если красная граница для внешнего и внутреннего фотоэффекта

соответственно равны , , то для них имеет место отношение:

Физический маятник представляет собой диск радиуса R и массой m, подвешенный за край (рис). Собственная частота колебаний маятника равна:

Привести в соответствие номера векторов (1, 2, 3, 4) на векторной диаграмме, построенной для механических вынужденных колебаний, с названием физических параметров характеризующих свойства колебательной системы:

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Разность фаз колебаний 2-х частиц, находящихся на расстоянии x1=20м и x2=30м, в плоской

бегущей волне с λ=40м, равна...

Тонкая плёнка одинаковой толщины освещается светом с частотами ν1 и ν2 < ν1. В проходящем свете в точке М наблюдается максимум интенсивности волны с частотой только ν1. В точке К будет наблюдаться максимум интенсивности волны с частотой:

Если время когерентности конечно, то с увеличением времени наблюдения (t) интерференции четкость интерференционной картины (разность между регистрируемыми значениями интенсивности в максимумах и минимумах):

Интенсивность плоской незатухающей волны:

Пять одинаковых источников, расположенных на одной прямой на расстоянии d друг от друга, излучают электромагнитные волны интенсивностью l0 каждая и длиной волны λ. Результирующая интенсивность в принимающем устройстве, удалённом на большое расстояние в направлении sinθ= λ/5d равна:

Если в плоской электромагнитной волне известно значение амплитуды электрического поля

, то значение амплитуды магнитного поля ( ) может быть определено по формуле:

Дифракция Фраунгофера имеет место при , где - масштаб неоднородности среды для волн, λ - длина волны, - расстояние от неоднородности до точки наблюдения. Условие вытекает из требования, чтобы

В приделах одного периода “системы элементов вещества” максимальный и минимальный потенциал ионизации, соответственно, имеют:

file:///D:/%D0%B1%D0%B0%D0%B7%D0%B0-%D1%84%D1%82...

Для упругих волн среду (2) считают более плотной, чем среда (1), если выполнены следующие условия. В этих выражениях ρ - плотность среды, z- волновое сопротивление.

Если умножить амплитуду магнитного поля на удельное волновое сопротивление вакуума, то получим:

Обобщенное уравнение свободных затухающих колебаний в линейных осцилляторах имеет вид: В уравнении:

Электрон движется в положительном направлении в одномерном потенциальном поле (рис).

Стоячая электромагнитная волна образуется при сложении двух встречных волн, электрические поля которых описываются функциями

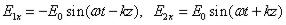. Соответствующие выражения для магнитных полей этих волн имеют вид:

На рисунке приведена векторная диаграмма затухающих колебаний в электрическом контуре с циклической частотой ω в момент времени t = τ, равный времени релаксации.Для построения векторной диаграммы в момент t = 0

Если переносимый фотонами импульс равен p, то длина волны λ электромагнитного