А. Р. Лакерник. Высшая математика.Краткий курс

VII. Кратные и криволинейные интегралы. Теория поля

4. Пусть в области (D) функция f (x,y) ³ 0. Тогда òò f (x,y)dxdy ³ 0,

1442443

³0

5.Пусть в области (D) функция f (x,y) ³ g(x,y) . Тогда

òòf (x,y)dxdy ³ òò g(x,y)dxdy,

¡ Из свойств абсолютных величин чисел следует, что

å f (Mi )Si £ å f (Mi )Si .

ii

Переходя в этом неравенстве к пределу при l ® 0 , имеем

19.Кратные интегралы

8.Аналогично случаю одной переменной доказывается следующая теорема.

Теорема 19.1. Если функция z = f (x,y) непрерывна в замкнутой

области (D) , то òò f (x,y)dxdy существует.

(D)

9. Теорема 19.2 (о среднем в двойном интеграле). Пусть z = f (x,y) непрерывна в замкнутой области (D) с площадью S. Тогда существует

такая точка (x0,y0)Î(D) , ÷òî òò f (x,y)dxdy = f (x0,y0 )S.

(D)

¡ Согласно теореме 19.1 интеграл òò f (x,y)dxdy существует. Пусть

(D)

m и M – наименьшее и наибольшее значения непрерывной функции f (x,y) в области (D) (см. теорему 12.2). Тогда при

Здесь 1 òò f (x,y)dxdy – это число, заключенное между двумя значе-

S (D)

ниями mи M функции f (x). Тогда согласно теореме 12.3 существует точ-

êà (x0,y0) (D) , такая, что f (x0,y0) = S1 (òòD)f (x,y) dxdy Þ

f (x0, y0)S = òò f (x,y) dxdy. x

(D)

10. Пусть z = f (x,y) непрерывна в замкнутой области (D) и в этой

области f (x,y) ³ 0. Согласно определению двойного интеграла 19.1 (который в данном случае существует в силу теоремы 19.1)

VII. Кратные и криволинейные интегралы. Теория поля

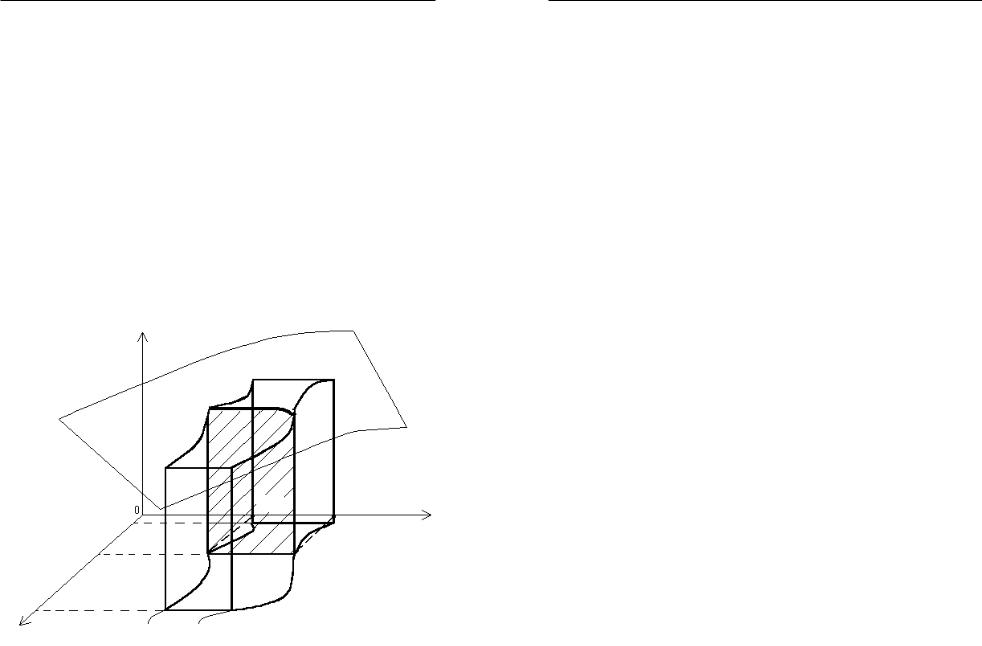
Впоследнейсуммеслагаемое f (Mi )Si –этообъемцилиндрасосно- ванием (Di ) и высотой f (Mi ) (рис. 94), а сумма таких слагаемых – это объем «ступенчатого» тела, состоящего из таких цилиндров .

y

Под объемом V тела, ограниченного областью (D) на плоскости 0xy, поверхностью z = f (x,y) и цилиндрической поверхностью, образующие которой параллельны оси 0z, а направляющей является граница области (D), будем понимать предел объемов таких ступенчатых тел при λ → 0 , если этот предел существует и не зависит от разбиения (D) на части и от выбора точек в каждой из частей. Но данный предел как раз и дает двойной интеграл, значит,

19.2. Вычисление двойного интеграла

Предположим, что в двойном интеграле òò f (x,y) область (D) яв-

(D)

ляется так называемой криволинейной трапецией, ограниченной прямыми x = a è x = b (a £ b) и кривыми y = ϕ(x) è y = ψ(x) , где обе эти функции непрерывны на отрезке [a, b] и y(x) ³ j(x), x О[a,b] (рис. 95). Такая область называется правильной в направлении оси 0y. Любая прямая, параллельная оси 0y, пересекает не вертикальную границу об-

19. Кратные интегралы

y

ная прямыми x = a è x = b (a £ b) и кривыми y = ϕ(x) è y = ψ(x) , где обе эти функции непрерывны на отрезке [a, b] и y(x) ³ j(x), x О[a,b], и пусть функция z = f (x,y) непрерывна в области (D). Тогда

¡ Функцию z = f (x,y) будем полагать непрерывной в замкнутой области (D), что согласно теореме 19.1 обеспечивает существование нашего двойного интеграла. Предположим еще, что в области (D) f (x,y) ³ 0, тогда для вычисления двойного интеграла можно применить формулу (19.2). Но согласно результатам разд. 10.8 объем тела можн о по-

b

считать и как интеграл от площади поперечного сечения: V = òS(x)dx

a

(отметим,чтопритакомрассуждениимыиспользуемравносильностьопределений объема, данных в разд. 10.8 и 19.1, что нуждается в строг ом

19.Кратные интегралы

Âпоследнем интеграле dx переставляют вперед и записывают эту формулу в виде

Докажем справедливость этой формулы в случае невыполнен ия условия f (x,y) ³ 0. Так как f (x,y) непрерывна в замкнутой области (D), значит, в этой области она ограничена и существует число C (в нашем случае отрицательное), такое, что f (x,y) ³ C Ю f (x,y) -C ³ 0 . Следовательно, только что выведенную формулу можно применить к ф ункции

Здесь S – площадь (D).

Приравнивая два полученных результата, убеждаемся в спра ведливости нужной нам формулы. x

Расстановка пределов в формуле (19.3) производится следующи м образом: x меняем от a до b, далее фиксируем произвольное значение x и проводим через точку x вертикальную прямую; вдоль этой прямой y меняется от минимального значения (или, как говорят, от точ ки «входа») ϕ(x) до максимального значения (или, как говорят, до точки «выхода») y(x) (см. рис. 95).

19.Кратные интегралы

4)пусть в области (T ) f (x,y,z) ³ 0 . Тогда

òòòf (x,y,z)dxdydz ³ 0,

(T )

если этот интеграл существует;

5) пусть в области (T ) f (x,y,z) ³ g(x, y,z) . Тогда

òòò f (x,y,z)dxdydz ³ òòò g(x,y,z )dxdydz.

той области (T), то òòò f (x,y,z)dxdydz существует.

(T )

Теорема 19.5 (о среднем в тройном интеграле). Пусть u = f (x,y,z) непрерывна в замкнутой области (T) с объемом V. Тогда существует такая

точка (x0,y0,z0) (T) , ÷òî òòò f (x,y,z)dxdydz = f (x0,y0,z0 )V .

(T )

¡ Согласно теореме 19.4 òòò f (x,y,z)dxdydz существует.

(T )

Пусть m и M – наименьшее и наибольшее значения непрерывной функции f (x,y,z) вобласти(T )(см.теорему12.2).Тогдапри(x,y,z) О (T)

VII. Кратные и криволинейные интегралы. Теория поля

Таким образом, число 1 òòò f (x,y,z)dxdydz заключено между дву-

V (T )

мя значениями функцииm и M. Тогда согласно теореме 12.3 существует точка (x0,y0,z0)О(T ), такая, что

Теорема 19.6. Пусть область (T) ограничена снизу и сверху гладкими или кусочно-гладкими поверхностями z = p (x,y) и z = q (x,y), проектирующимися на плоскость 0xy в некоторую ограниченную область (D), p(x,y) ≤ q(x,y), (x,y) (D) , а сбоку – цилиндрической поверхностью с образующими, параллельными оси 0z , и границей области (D) в роли направляющей (рис. 102) . Пусть также функция u = f (x,y,z) непрерывна в области (T). Тогда

z

z = q (x,y)

z = p (x,y)

y

19. Кратные интегралы

¡ Разобьем область (D) гладкими или кусочно-гладкими кривыми на части (Di ) с площадями Si и рассмотрим цилиндры с основаниями (Di ) и образующими, параллельными оси 0z. Пусть

Разобьем отрезок [m,M ] на части точками zk и проведем плоскости z = zk . Обозначим Dzk = zk+1 - zk . Тогда плоскости z = zk разобьют наши цилиндры на более мелкие, которые будем обозначать д вумя ин-

дексами, а именно: (Tik ) = {(x,y,z):(x,y)Î(Di ), z Î[zk ,zk+1]} . Тем самым мы разбили область (T) на части (Tik ) с объемами Vik = Si zk .Îäíà

из таких частей изображена на рис. 102.

Как обычно, через l обозначим наибольший (по i и k) диаметр областей (Tik ) . Будем предполагать, что число l достаточно мало. Тогда части, расположенные около верхней и нижней границ, тоже м ожно заменить на цилиндры указанного вида (это является следс твием стремления к 0 при l ® 0 интеграла по данным частям).

Преобразуем правую часть формулы (19.6):

=åDzk òò f (x,y,zk )dxdy.

i,k (Di )

VII. Кратные и криволинейные интегралы. Теория поля

К каждому из последних интегралов применим теорему 19.2 о среднем:

Но последняя сумма является одной из интегральных сумм дл я тройного интеграла в левой части формулы (19.6) (этот интегра л существует в силу непрерывности подынтегральной функции). Зн ачит, при достаточно малых λ эта сумма сколь угодно мало отличается от самого интеграла. Таким образом, правая и левая части формулы (19.6) с коль угодно близки, т.е. совпадают. x

Подведем итог, пользуясь не вполне математическим, но зат о доступным языком: в формуле (19.6) пределы расставляются для тре хмерной области (T ), представляющей собой параллельную оси 0z «цилиндрическую банку» с двумя «крышками» – нижней z = p (x,y) и верхней z = q (x,y); при расстановке пределов х и y меняются по проекции (T ) на плоскость 0xy, а z меняется от нижней до верхней «крышки». При таком рассуждении часто можно, не рисуя область (T ), обойтись плоским чертежом области (D).

При вычислении тройного интеграла по формуле (19.6) сначала

q(x,y)

находим интеграл ò f (x,y,z ) dz, который зависит от х и y, а потом

p(x,y)

двойной интеграл от полученной функции по области (D).

Если область (D) является криволинейной трапецией, изображенной на рис. 95, то согласно теореме 19.3 можно расставить и преде лы по x и y, получив результат

by( x) q( x,y)

19. Кратные интегралы

Пример 1. Расставить пределы в тройном интеграле òòò f (x,y,z)dxdydz,

(T )

где область (T ) ограничена поверхностями x = 0, y = 0, z = 0, x + y + z = 1.

Ð å ø å í è å

Пространственный чертеж области (T ) (без которого можно и обойтись) и чертеж ее проекции на плоскость 0xy имеют вид, представленный на рис. 103 и 104.

1

x

Используя формулы (19.6) и (19.7), расставим пределы интегрирования:

Пример 2. Найти объем тела, ограниченного поверхностями y = x, y = 2x, x = 1, z = x2 + y2, z = x2 + 2y2.

VII. Кратные и криволинейные интегралы. Теория поля

=7 x4 1 = 7 .

3 4 0 12

19.5.Замена переменных в двойном интеграле

Рассмотрим òò f (x,y)dxdy , где область (D ) ограничена гладкой или

(D)

кусочно-гладкой кривой, а функция z = f (x,y) непрерывна в этой об-

ласти. Пусть x = x(u,v), y = y(u,v), где эти функции осуществляют взаимно однозначное и в обе стороны непрерывно дифференциру емое соответствие между точками области (D) на плоскости 0xy и точками некоторой области (D¢) на плоскости 0′uv (это означает, что каждой точке одной из этих областей соответствует одна, и только одна точка другой и функции x = x(u,v), y = y(u,v) è u = u(x,y), v = v(x,y) имеют непрерывные частные производные в соответствующих област ях). Можно показать, что при этом границе одной из этих областей со ответствует граница другой, и наоборот.

Так как функция z = f (x,y) непрерывна в области (D), то òò f (x,y)dxdy существует, поэтому для его вычисления, как предела

(D)

интегральных сумм, можем эти суммы выбирать наиболее удоб ным для нас способом: пренебрегая частями у границы (что можно сде лать, так как интегралы по этим частям стремятся к 0 при λ → 0 ), разобьем область (D¢) на прямоугольники линиями u = const, v = const, при этом и область (D) разобьется на некоторые подобласти. Рассмотрим один из таких прямоугольников (рис. 107) и соответствующий ему (огра ниченный сплошной линией) «криволинейный четырехугольник» (р ис. 106) на плоскости 0xy ( Dx и y достаточно малы).

Возьмем в этой области точку P1(x,y) , соответствующую точке

P1′(u,v) , ò.å. P1(x(u,v),y(u,v)) = P1(x,y) . На рис. 106 и 107 точке P2′(u + u,v) соответствует точка P2(x(u + u,v),y(u + u,v)) , точке

19. Кратные интегралы

ные производные, то эти функции дифференцируемы. Вспомним , что для любой дифференцируемой функции g(x,y) согласно определению 12.21 и теореме 12.6

ãäå α, β → 0 ïðè u, v → 0 . Пренебрегая в этой формуле членами более высокого порядка малости α u è β v и опуская (как и для точки P1) аргументы u и v, получим приближенные значения координат то- чек Pi , i = 2, 3, 4 :

здесь v = 0,

Находя координаты вектора как разность координат конца и нача- ла, имеем

19. Кратные интегралы

(D)

x + y = 1, x + y = 2, 2x – y = 1, 2x – y = 3 (ðèñ.108). Ð å ø å í è å

Расстановка пределов по параллелограмму (D), как легко понять, приведет к трем слагаемым, поэтому проще сделать замену: x + y = u, 2x – y = v.

дет в прямоугольник (D ′), ограниченный прямыми u = 1, u = 2, v = 1, v = 3 (ðèñ. 109).

VII. Кратные и криволинейные интегралы. Теория поля

19.6. Двойной интеграл в полярных координатах

Как частный случай формулы (19.9) рассмотрим переход в двойно м интеграле к полярным координатам по формулам x = r cosj , y = r sinj . Якобиан этих функций имеет вид

Соответственно формула перехода приобретает вид

Чтобы расставить пределы в последнем интеграле, нужно, чт обы область (D′) на«плоскости» r,j былакриволинейнойтрапецией(рис.110).

Последний чертеж можно перенести на плоскость 0xy. Область интегрирования при этом должна быть ограничена линиями j = a и ϕ = β (это два луча, проведенные из начала координат) и двумя кри выми, заданными в полярной системе координат: r = r1(ϕ) è r = r2(ϕ) , ãäå r2(j) ³ r1(j) (ðèñ. 111).

19. Кратные интегралы

r = r2 (j)

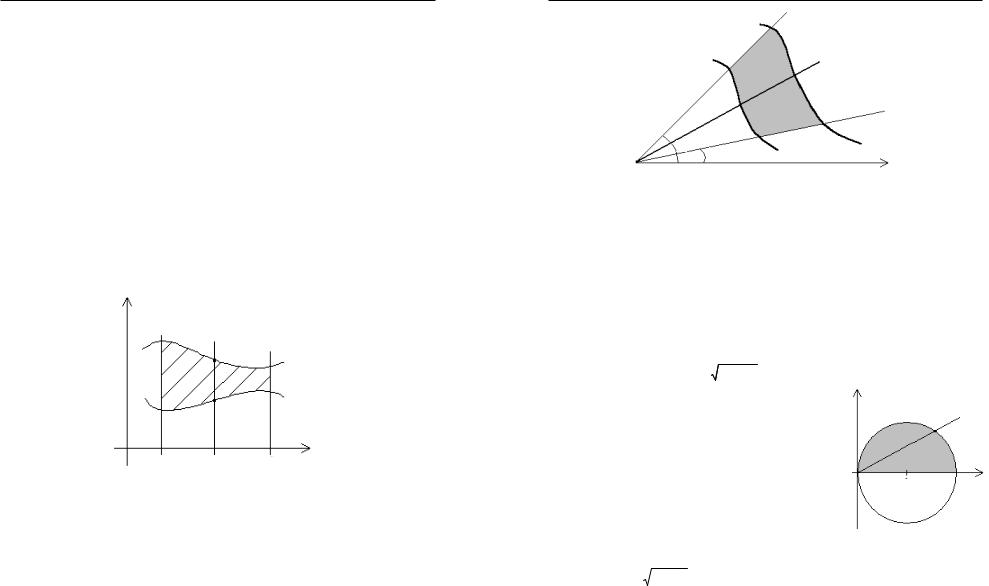
Пользуясь рис. 111, расставим пределы в полярных координатах следующим образом: j меняем от a до b, теперь фиксируем угол j , т.е. проводим луч из начала координат, вдоль этого луча r меняется от минимального значения (точки «входа») r1(j) до максимального значения (точки «выхода») r2(j).

К полярным координатам стоит переходить, если уравнение г раницы области или, может быть, подынтегральная функция сод ержат выражение x2 + y2 , которое в этих координатах превращается в r2 cos2 j + r2 sin2 j = r2 .