
Х-210801 / материалы для самостоятельного изучения некоторых разделов курса / Фрагменты лекций / Изотермы идеальных и реальных газов. Фугитивность
.docРасчет термодинамических функций гомогенной однокомпонентной системы, если система − реальный газ вида k
Изотермы идеального и реального газов. Фугитивность

В физике газ, состоящий из молекул точечного размера невзаимодействующих между собой, принято называть идеальным.
Для полного описания свойств данного количества газа нужно было бы измерить такие величины, как давление, объем, плотность массы, показатель преломления, температуру, теплопроводность и т.д. Однако экспериментально установлено, что достаточно определить только две из этих величин, все остальные также будут однозначно определены.
Для идеального газа известно уравнение состояния:
![]() или
или
![]() (1)
(1)
Это уравнение Клапейрона-Менделеева, объединившее законы идеальных газов Бойля-Мариотта, Гей-Люссака-Шарля , Авагадро.
Еще один закон для идеальных газов – это закон Дальтона, согласно которому полное давление смеси газов равно сумме парциальных давлений газов в смеси. Парциальным давлением газа называется давление, которое газ оказывал бы, если бы один заполнял объем сосуда при заданной температуре.
Закон Дальтона легко выводится из уравнения состояния идеального газа. Общее число молей газа в смеси (n) равно сумме чисел молей отдельных газов:
![]() (2)
(2)
Умножая
(2) на
![]() (где V
– объем сосуда), получим:
(где V
– объем сосуда), получим:
![]() т.е.
т.е.
![]() (3)
(3)
![]() (4) − парциальное
давление газа вида k.
(4) − парциальное
давление газа вида k.
![]() (5) − общее давление
в газовой смеси
(5) − общее давление
в газовой смеси
Разделим (4) на (5)
![]() (6)
(6)
Из закона Дальтона следует, что доля общего давления, приходящегося на данный газ, равна той доле, которую составляет число молей этого газа по отношению к общему числу молей, т.е. мольной доле.
Следовательно, парциальное давление газа можно определить как
![]() (7)
(7)
Это тоже закон Дальтона.
Для идеального газа отношение
![]() (8)
(8)
Величина z − это фактор сжатия (или фактор сжимаемости).
Реальные газы не описываются точно уравнениями состояния идеального газа. Лишь тогда, когда давление мало или температура велика –тогда свойства реального газа близки к свойствам идеального газа. Свойства идеальных и реальных газов отличаются из-за наличия взаимодействия между молекулами.
С войства
идеальных и реальных газов отличаются
из-за наличия взаимодействия между
молекулами газа. Силы отталкивания
способствуют расширению газа, силы
притяжения – сжатию. Силы отталкивания
существенны, когда молекулы расположены
близко друг к другу(молекулярные
диаметры) это случай высоких давлений,
т.е. когда много частиц занимают малый
объем. Силы притяжения , напротив,
эффективны когда молекулы близко, но
не касаются друг друга(несколько
молекулярных диаметров).
войства
идеальных и реальных газов отличаются
из-за наличия взаимодействия между
молекулами газа. Силы отталкивания
способствуют расширению газа, силы
притяжения – сжатию. Силы отталкивания
существенны, когда молекулы расположены
близко друг к другу(молекулярные
диаметры) это случай высоких давлений,
т.е. когда много частиц занимают малый
объем. Силы притяжения , напротив,
эффективны когда молекулы близко, но
не касаются друг друга(несколько
молекулярных диаметров).
При низких температурах силы межмолекулярных взаимодействий возникают потому что из-за малых скоростей движения молекулы находятся друг с другом относительно долго.
При низких давлениях и высоких температурах молекулы газа находятся далеко друг от друга и силы межмолекулярного взаимодействия не играют большой роли и газ ведет себя как идеальны. При умеренных давлениях преобладают силы притяжения, поэтому сжимаемость газа будет больше чем у идеального газа( силы межмолекулярного взаимодействия будут способствовать сближению. При высоких давлениях силы отталкивания будут препятствовать сближению молекул и газ будет менее сжимаем.
Для реальных газов фактор сжатия отличается от единицы. Если z < 1, значит, реальный газ более сжимаем, чем идеальный газ.
При низких температурах силы межмолекулярных взаимодействий возникают потому что из-за малых скоростей движения молекулы находятся друг с другом относительно долго.
При низких давлениях и высоких температурах молекулы газа находятся далеко друг от друга и силы межмолекулярного взаимодействия не играют большой роли и газ ведет себя как идеальны. При умеренных давлениях преобладают силы притяжения, поэтому сжимаемость газа будет больше чем у идеального газа( силы межмолекулярного взаимодействия будут способствовать сближению. При высоких давлениях силы отталкивания будут препятствовать сближению молекул и газ будет менее сжимаем.
Для реальных газов фактор сжатия отличается от единицы. Если z < 1, значит, реальный газ более сжимаем, чем идеальный газ.
В лияние
температуры на фактор сжатия видно из
следующего рис.
лияние
температуры на фактор сжатия видно из
следующего рис.
Если создать достаточно низкую температуру , то приложив внешнее давление, можно настолько уменьшить объем газа, что сила притяжения между молекулами оказывается достаточной, чтобы вызвать конденсацию. Ниже некоторой температуры (критическая температура) между жидкостью и паром существует граница раздела – мениск. При критической температуре мениск исчезает, при этом жидкость и газ становятся настолько сходными, что нет раздельных фаз. Критическое давление – это давление при критической температуре.
Вид кривых зависимости давления для случая изопентана от объема вблизи критической температуры приведен на рис.3

Рис.1
Рассмотрим отличие изотерм идеального и реального газов (рис.1). Верхние изотермы – это изотермы идеального газа, они соответствуют уравнению Менделеева-Клапейрона, кривые всегда однозначны. Остальные изотермы соответствуют уравнению Ван дер Вальса.Для реального газа тоже известно несколько уравнений состояния.
Уравнение
ВандерВаальса
![]() (9), которое можно также записать и в
виде
(9), которое можно также записать и в
виде
![]() (10)
(10)
Изотерма Tкр, соответствует температуре, называемой критической . На этой изотерме имеется точка перегиба (461 К) , давление в этой точке называется критическим давлением, а мольный объем – критическим мольным объемом. Изотермы, расположенные при более низких температурах уже имеют вид, сильно отличающийся от изотермы идеального газа. У них имеется участок, с так называемой многозначной зависимостью p-v, т.е. одному давлению соответствует не одно значение объема. Эти изотермы соответствуют ситуации, когда возможно сжижение газа, т.е. переход газа в жидкое состояние. На горизонтальном участке изотермы в системе находится равновесная смесь и газа и жидкости. Они разделены мениском (если рассматривать какую-то емкость), т.е. есть граница раздела.
Изогнутые штриховые линии – это так называемые петли Ван дер Ваальса, они расчетные, поскольку уравнение Ван дер Ваальса описывает кубическую кривую (мольный объем), имеющую при температуре ниже критической два экстремума. При увеличение температуры эти экстремумы сближаются, и при температуре, равной критической сливаются.
В критической точке нет различия между газом и жидкостью. Давление, при котором исчезает различие между жидкостью и газом называется критическим давлением, мольный объем –критическим мольным объемом, температура –критической температурой, а все вместе- критическими параметрами.
Для каждого газа существуют свои критические параметры.
Коэффициенты уравнения Ван дер Вальса находят подгонкой расчетных кривых к экспериментальным.
Критические параметры определяются экспериментально, но они также связаны с константами в уравнении Ван дер Ваальса. Поскольку в точке перегиба на критической изотерме первая и вторая производные обращаются в нуль, можно получить:
![]() ;
;
![]() ;
;
![]()
При высоких температурах и низких давлениях реальный газ близок по свойствам к идеальному: RT настолько велико, что вторым слагаемым в уравнении (2) можно пренебречь, а в знаменателе первого, можно пренебречь величиной b, т.к. мольный объем достаточно велик.
Выше критической температуры газ не сжижается! Газ можно перевести в жидкость только при температуре, ниже критической. Газ, находящийся в равновесии с жидкостью называется насыщенным паром. Термин «давление насыщенного пара» - это давление газа вещества k, находящегося в равновесии с жидкостью вида k.
К критической точке можно подойти и со стороны жидкости. Если ее нагревать в закрытом сосуде, то при критической температуре плотности жидкости и равновесного с ней пара будут одинаковы, т.е. между жидкостью и паром исчезнет различие. При температуре выше критической в закрытом сосуде существует единственная фаза вещества, называемая сверхкритическим флюидом.
Из курса физики известно, что идеальный газ, это газ, в котором можно пренебречь, как размерами молекул, так и силами взаимодействия между ними. Реальный газ − это газ, в котором такие пренебрежения делать нельзя. Т.е. нужно учитывать и размеры молекул и силы взаимодействия размерами молекул между ними.
В курсе физической химии получено очень важное уравнение, характеризующее мольную энергию Гиббса для идеального газа вида k:
![]() (11)
(11)
Из этого уравнения оказалось возможным получить уравнения для расчета всех остальных термодинамических функций идеального газа.
С точки зрения физической химии идеальным называется газ, для которого выполняется зависимость мольной энергии Гиббса от температуры и давления в виде уравнения (11).
При переходе от описания идеальных газов к характеристике реальных объектов, т.к. к реальным газам, хотелось бы по возможности, сохранить и подход и формы выражений, полученных для идеальных систем.
Уравнение (11) было получено из соотношения
![]() v
v![]() (12)
dg
(12)
dg![]() = v
= v![]() (p)
dp
(T
=const)
(p)
dp
(T
=const)
Зная уравнение
состояния идеального газа, мы выражали
из него v![]() (p)
(p)
и получали затем уравнение (11).
Если воспользоваться
одним из этих приближенных уравнений
и выразить v![]() = f(p)
(12), то получим выражения, которые
будет трудно использовать при расчетах.
= f(p)
(12), то получим выражения, которые
будет трудно использовать при расчетах.
Л ьюис
подошел к решению задачи совершенно
другим путем.
ьюис
подошел к решению задачи совершенно
другим путем.
ЛЬЮИС
Джилберт
Ньютон
1875− 1946
Зависимость мольной энергии Гиббса реального газа от давления изображается кривой (рис.1)
Мольная энергия Гиббса реального газа abcd
Мольная энергия Гиббса идеального газа abcе
Участок ab
при р0,
![]() .
.
Участок bc
преобладают
силы притяжения
![]()
Участок cd
преобладают
силы отталкивания
![]()
Чтобы использовать уравнение (11) для описания этой кривой, Льюис предложил заменить в нем истинное давление p на эффективное, называемое фугитивностью f.
Вообще Льюис предложил для реальных систем использовать тот же вид термодинамических уравнений, что и для идеальных, заменяя в них одни переменные (давления в случае газов и концентрацию в случае растворов) на другие.
Пока остановимся на газах. Итак Льюис предложил вместо давления газа вида k использовать новую переменную - фугитивность газа вида k. Фугитивность это функция, зависящая от давления и температуры. Она определяется таким образом, чтобы точно выполнялось соотношение
![]() ,
(13)
,
(13)
где
![]()
стандартная фугитивность, совпадающая
с
стандартная фугитивность, совпадающая
с
![]() или [p]
или [p]
Стандартное состояние реального газа вида k при любой Т − это состояние гипотетического идеального газа при давлении (фугитивности) 1 бар (1атм).
![]() .
(14)
.
(14)
![]()
фугитивность
(летучесть);
фугитивность
(летучесть);
![]()
коэффициент фугитивности.
коэффициент фугитивности.
Мольная энергия Гиббса реального газа
![]() (15)
(15)
Р асчет
фугитивности и коэффициента фугитивности
асчет
фугитивности и коэффициента фугитивности
При понижении давления реального газа его свойства приближаются к свойствам идеального газа.
Если p* очень мало, то f = f* =p*.
Рассмотрим переход от состояния идеального газа к состоянию реального газа
1. расширим идеальный газ до давления p* по изотерме 12.
2. сожмем до давления р по изотерме реального газа 23.
Изменение энергии Гиббса при этом:
![]() (16)
(16)
Энергия Гиббса реального газа в точке 3:
![]() ; (17) Энергия
Гиббса идеального газа в точке 1:
; (17) Энергия
Гиббса идеального газа в точке 1:
![]() (18)
(18)

 (19)
(19)
![]()
![]() =
=
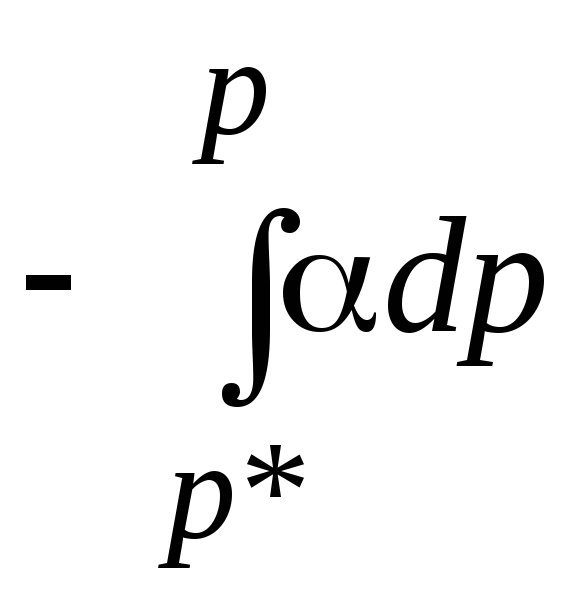 (21);
(21);
![]() =
=
![]() (22)
(22)
Величина коэффициента фугитивности связана с изменением энергии Гиббса в обратимом процессе перехода системы из идеального состояния в реальное при постоянных значениях температуры и давления.
Величину f
и
![]() находят либо графически по рис., взяв
интеграл, либо расчетом.
находят либо графически по рис., взяв
интеграл, либо расчетом.
