2. В идеальном совершенном растворе за стандартное состояние любого компонента k раствора принимают его состояние в виде чистого вещества.

. (7)

Выражение для химического потенциала компонента k в этом растворе будет иметь следующий вид:

. (8)

Идеальные совершенные растворы – это растворы, в которых и растворитель и растворенные вещества обладают сходным химическим строением и имеют близкие термодинамические характеристики, например растворы оптических изомеров, или растворы изотопов.

Выражение для химического потенциала компонента реального газового раствора будет таким же как (6). В качестве концентрации для жидких растворов помимо N –шкалы используются с и d шкалы, т.е. активность компонента может быть выражена как

; ; .

Идеальный предельно - разбавленный раствор – это раствор, в котором невозможно достичь больших концентраций одного из компонентов , например, раствор солей. В такой модели идеального раствора стандартные состояния для растворителя и растворенных веществ различны.

Стандартное состояние растворителя как компонента раствора определяется его состоянием в чистом виде. Выберем стандартное состояние растворителя (часто растворитель обозначается как компонент 1) в некотором растворе. Пусть единицей концентрации является мольная доля

, (9)

где  число молей компонента 1 (растворителя);

 число молей всех компонентов раствора.

Активность растворителя из формулы (16) равна:

, (10)

где  активность растворителя;

 коэффициент активности растворителя в шкале мольных долей.

Стандартное состояние выбирается таким образом, чтобы активность растворителя стала равна мольной доле его, когда мольная доля приближается к единице, или математически

. (11)

Поскольку =, то (11) можно выразить как

.

Выбор определяет стандартное состояние, при котором активность равна единице. Для жидкого раствора стандартное состояние растворителя определяется как чистая жидкость. Пример  это разбавленные водные растворы, для которых =1. При написании многих уравнений равновесий в водных растворах традиционно исключается активность воды, т.к. для растворителя используется активность в шкале мольных долей, а в разбавленных растворах и .

Итак, для активности растворителя используются следующие выражения:

Очень разбавленный раствор: = 1;

Разбавленный или идеальный раствор: ;

Реальный раствор: .

Уравнение соответствует идеальному раствору: при любой концентрации растворитель имеет те же свойства, что и в разбавленном растворе.

Стандартнее состояние растворенного вещества в этом случае определяется как экстраполированное состояние, когда концентрация равна 1, а свойства  те, что экстраполированы из очень разбавленных растворов. Стандартное состояние растворенного вещества  это гипотетическое состояние в том смысле, что оно соответствует единичной концентрации идеального раствора (молярной или моляльной).

Активность растворенного вещества () может быть выражена в разных концентрационных шкалах: Nшкале (шкала мольных долей), с шкале (шкала молярностей), d или m шкале (шкала мольно-массовых отношений или шкала моляльности) .

Рассмотрим случай, когда активность растворенного вещества выражена в шкале молярности, т.е. в сшкале.

,

где  активность растворенного вещества; в случае двухкомпонентного раствора эту величину обозначают , т.к. 1-й компонент это растворитель;

 коэффициент активности растворителя в шкале молярности ;

 молярная концентрация растворенного вещества, моль/л.

Стандартное состояние в шкале молярности выбрано так, что активность равна концентрации, когда концентрация стремится к нулю:

; .

На рис. 1 приведены концентрационные зависимости активности растворенного вещества (сплошная линия) и активности идеального раствора (пунктирная линия), экстраполированного из очень разбавленного раствора.

Из рис. 1 видно, что стандартное состояние в шкале молярности (для растворенного вещества)  это точка, лежащая на экстраполированной прямой идеального раствора.

Стандартное состояние растворенного вещества должно соответствовать следующим требованиям:

1. если 0, то ;

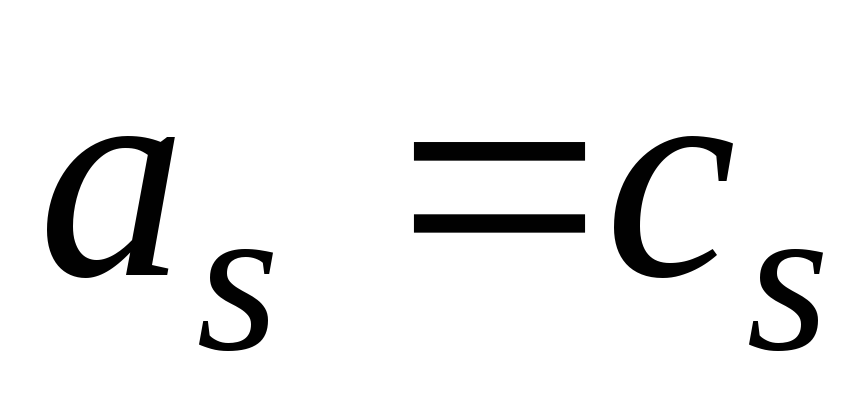2. в стандартном состоянии .

На рис. 2 приведены зависимости химического потенциала растворенного вещества от логарифма молярности для реального раствора (сплошная линия) и для идеального раствора, экстраполированного из очень разбавленного раствора (пунктирная линия).

Для определения стандартного химического потенциала растворенного вещества нужно получить зависимость химического потенциала от натурального логарифма концентрации растворенного вещества и проэкстраполировать эту линию к состоянию, когда концентрация равна единице, т.е. ln с_s= 0.

Тогда мы получим (рис.2). Таким образом, стандартное состояние растворенного вещества  это состояние, в котором проявляются свойства очень разбавленного раствора, проэкстраполированного к единичной концентрации. Это гипотетическое состояние, а не реальный раствор, который можно приготовить.

Другой часто используемой единицей концентрации является моляльность m_s (или d_s - мольно массовые отношения, dшкала)  это число молей растворенного вещества на единицу массы растворителя.

Активность вещества в шкале моляльности равна

, (25)

где  активность растворенного вещества;

 коэффициент активности растворителя в шкале моляльности ; или возможно обозначение ;

или  молярная концентрация растворенного вещества или мольно-массовое отношение растворенного вещества.

Применение моляльности идентично применению молярности.

Разбавленный или идеальный раствор: ;

Реальный раствор: .

Стандартное состояние это экстраполированное состояние; стандартный химический потенциал получается при линейной экстраполяции химического потенциала измеренного в разбавленном растворе, в единичной моляльности. Моляльность используется вместо молярности при самых точных термодинамических измерениях. Поскольку моляльность определяется весом, а не объемом, ее измерения более точно и она не зависит от температуры. Для разбавленных водных растворов 1 л раствора практически содержит 1 кг воды, поэтому численные значения молярности и моляльности очень близки.

Следует отметить, что коэффициенты активности в разных концентрационных шкалах связаны между собой определенными математическими соотношениями и имеют разную величину для одного и того же раствора. Так, например, зависимость между коэффициентами активности какого-либо вещества в N шкале и в mшкале в водных растворах описывается уравнением:

.

Очевидно чем больше концентрация раствора, тем больше разница между коэффициентами активности в различных концентрационных шкалах.

Биохимические стандартные состояния

Рассмотрим некоторую биохимическую реакцию, которая включает ион трехосновной кислоты H₂A^. Реально в растворе могут существовать кроме названного также ионы HA^2 ; A^3 заряженные частицы H₃A. Соотношение их существенно зависит от величины рН, и концентрацию иона H₂A^ трудно определить.

Важная особенность биохимического стандартного состояния заключается в том, что оно рассматривается при величине рН=7, который близок к физиологическому рН и это является стандартным значением активности ионов водорода.

Следовательно , для концентрации H⁺ = 10^7 моль/л.

Активность любой другой молекулы равна общей концентрации всех модификаций этой молекулы при рН=7: (при рН=7), т.е. в нашем примере это общая концентрация трехосновной кислоты, определяемая аналитически. При этом раствор рассматривается как идеальный.