Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

расчет изменений некоторых функций при протекании идеальной газовой реакции

.doc

Скачиваний:

Добавлен:

23.02.2015

Размер:

375.81 Кб

Скачать

☆

Изменение экстенсивных свойств системы в ходе химической реакции

Химическое превращение – это процесс преобразования одних компонентов в другие. При этом происходит изменение чисел молей компонентов.

Все термодинамическое описание системы с протекающей в ней химической реакцией будет строиться на использовании уравнения для химического потенциала компонента системы ( мольной энергии Гиббса)

для всех систем

для идеальной газовой системы

Рассмотрим смесь нескольких компонентов (в закрытой системе), среди которых возможна химическая реакция, описываемая уравнением

. (1)

Множители перед символами химических элементов или соединений называются стехиометрическими коэффициентами компонентов 1, 2, ... , .

Сами компоненты принято называть исходными веществами, если они стоят в уравнении реакции слева, и продуктами реакции, если они расположены в уравнении реакции справа.

Вместо стехиометрических коэффициентов в уравнениях термодинамики принято учитывать стехиометрические числа, которые для продуктов реакции равны стехиометрическому коэффициенту с положительным знаком для продуктов реакции, а для исходных веществ − стехиометрическому коэффициенту с отрицательным знаком. Стехиометрические коэффициенты всегда положительны, а стехиометрические числа различаются по знаку, в зависимости от того, исходным веществом или продуктом является данный компонент.

Для описания равновесий в системах с химическим превращением используют глубину реакции, обозначаемую греческой буквой (кси):

, (2)

где величина – изменение числа молей компонента в результате химического превращения:

, (3)

где – число молей компонента в любой момент времени, кроме начального; – число молей компонента в начальный момент времени, когда химического превращения еще нет и глубина реакции равна нулю.

Если количество молей исходных веществ, равное их стехиометрическим коэффициентам, перешло в такое количество молей продуктов, которое тоже равно стехиометрическим коэффициентам, то говорят, что реакция совершила один пробег, а математически это можно записать как =1. Таким образом, глубина химической реакции измеряется в молях. Приращение глубины реакции можно представить как

. (4)

Рассмотрим зависимость некоторого экстенсивного свойства, которое обозначим , в общем виде, а затем полученные уравнения запишем для конкретных экстенсивных величин .

Выберем в качестве переменных, относительно которых мы будем рассматривать зависимость экстенсивных свойств от глубины химической реакции, следующие: давление, температуру, числа молей всех компонентов системы:

Если (5) ,

Образуем полный дифференциал экстенсивного свойства :

. (6)

При проведении реакции в условиях постоянства давления и температуры

. (7)

Для того чтобы найти зависимость экстенсивного свойства Е от глубины химической реакции, продифференцируем (7) по глубине химической реакции в условиях постоянства давления и температуры:

. (8)

В правой части уравнения (8) под знаком суммы записано произведение двух величин. Первый сомножитель – это частная производная экстенсивного свойства по числу молей компонента k в условиях постоянства температуры, давления и остального состава, т. е. парциальная мольная величина экстенсивного свойства Е, которая обозначается следующим образом:

. (9)

 парциальное мольное свойство компонента k участника

реакции, зависящее от глубины протекания реакции.

Второй сомножитель равен стехиометрическому коэффициенту:

. (10)

Подставляя (9) и (10) в выражение (8), можно получить:

. (11)

Величина, стоящая в (11) справа, называется дифференциальным мольным изменением экстенсивного свойства Е за счет протекания химической реакции.

Для того чтобы вычислить интегральное изменение экстенсивного свойства Е, которое произошло в результате химической реакции надо проинтегрировать (11). Причем нижним пределом интегрирования считают состояние, при котором глубина реакции равна нулю, а верхним пределом – состояние, при котором глубина реакции достигнет величины x:

Следовательно, для того чтобы рассчитать изменение какого-либо свойства при протекании химической реакции, надо знать стехиометрическое уравнение реакции и величину парциальных мольных свойств каждого компонента в любой момент протекания реакции. Поскольку при изменении глубины реакции постоянно меняется состав, то необходимо найти зависимость парциального мольного свойства от изменяющегося состава. Эту проблему решают при помощи такого приема: представляем парциальное мольное свойство вещества k в виде суммы двух слагаемых, одно из которых назовем стандартным мольным свойством и будем рассматривать его зависящим только от давления и температуры, а второе слагаемое будем считать связанным с изменением свойства E за счет образования смеси реагирующих веществ вместо нескольких отдельно существующих чистых веществ. Это второе слагаемое как раз и будет зависеть от концентрации образующегося раствора. Тогда парциальное мольное свойство можно выразить следующим образом:

или (11)  (9)

 мольное свойство чистого компонента k ;  парциальная мольная функция смешения свойства Е.

По формуле (11) делают приближенный расчет: определяют лишь первое слагаемое и пренебрегают вторым.

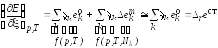
То есть, говоря об изменении свойства Е при протекании химической реакции, рассчитывают величину изменения стандартного мольного свойства Е, которое произошло в результате химической реакции,:

. (12)

Если в качестве стандартного выбрать состояние чистого вещества, то обозначение стандартного мольного свойства будет иным: .

Поскольку << ,

 стандартное мольное изменение экстенсивного свойства Е за счет протекания химической реакции

… в идеальном совершенном растворе

 … в идеальном газовом растворе

Изменение некоторых функций при протекании газовой реакции

в смеси идеальных газов

Зависимость энергии Гиббса реакции r от глубины реакции

По мере протекания химической реакции в условиях постоянства давления и температуры, как было показано ранее критерием её самопроизвольности является энергия Гиббса. И по мере протекания реакции энергия Гиббса уменьшается, становясь минимальной в момент равновесия. На рисунке показана эта зависимость.

Запишем выражение для определения дифференциального мольного изменения энергии Гиббса за счет протекания реакции

(1)

Очевидно, что величина дифференциального мольного изменения энергии Гиббса равна производной (2)

При равновесии

(3)

При самопроизвольной реакции

(4)

Исходя из молекулярных представлений, минимум энергии Гиббса, соответствующий , может быть связан с энергией Гиббса смешения.

Например, рассмотрим гипотетическую газовую реакцию A = B, в которой молекулы А превращаются в молекулы В без смешения. В этом случае энергия Гиббса системы изменится от до пропорционально количеству образующегося продукта В. При этом зависимость будет прямолинейной, и наклон на любой стадии будет неизменным и равным . Если же учитывать процесс смешения образующихся молекул В с оставшимися молекулами А, то нужно учесть вклад процесса смешения в полное изменение энергии Гиббса, который описывается уравнением:

Это выражение дает U− образный вклад в полное изменение энергии Гиббса системы. При суммировании кривой смешения с прямой линией реакции получается несимметричная кривая с минимумом, который соответствует равновесному составу реакционной смеси.

По мере образования продуктов, увеличивается вклад, вносимый энергией Гиббса смешения.

Для расчета изменения энергии Гиббса за счет протекания реакции используют формулу (5)

Где парциальная мольная энергия Гиббса компонента k идеальной газовой смеси совпадает с химическим потенциалом компонента k в реакционной смеси . (6)  (5)

(7)

где  стандартная мольная энергия Гиббса газовой реакции

Уравнение (7) − уравнение изотермы ВантГоффа

Зависимость энтропии реакции r от глубины реакции

(8)

Парциальная мольная энтропия компонента k идеальной газовой

смеси (9)  (8)

(10)

где  стандартная мольная энтропия газовой реакции

Зависимость энтальпии реакции r от глубины реакции

(11)

Парциальная мольная энтальпия компонента k идеальной газовой смеси (12)  (11)

где  стандартная мольная энтальпия газовой реакции

(13)

Расчет стандартных мольных изменений экстенсивных свойств в реакции между идеальными газами

Расчет стандартного мольного изменения энтропии

Энтропия – это функция, стандартные мольные изменения которых за счет протекания реакции можно найти по формуле

(1)  мольная энтропия чистого газообразного вещества k (справочная величина, при 298 К).

Известно, что у энтропии вещества k возможно рассчитать абсолютное значение

В справочниках приводятся значения энтропий индивидуальных веществ при температуре 298 К и p = 1 атм для жидких и кристаллических веществ. Для газообразных веществ указаны , то есть [p] = 1 атм, причем .

(2)

При другой температуре:

(3)

Изменение мольной изобарной теплоемкости системы в результате протекания реакции при любой температуре Т находится из выражения:

 стандартная мольная изобарная теплоемкость реакции

Зависимость стандартной мольной энтропии реакции от температуры

(4)

Разделяя переменные и интегрируя, получим?

(5)

 Расчет стандартного мольного изменения энтальпии за счет протекания реакции

(6)

Стандартные мольные энтальпии и функции Гиббса чистых веществ найти невозможно, так как нельзя определить абсолютное значение внутренней энергии вещества, а, следовательно, и любых других термодинамических функций, включающих внутреннюю энергию. Поэтому для расчета, например, стандартной мольной теплоты реакции обычно прибегают к линейным комбинациям стандартных мольных теплот других реакций . В качестве исходных реакций для такого рода комбинаций обычно используют реакции образования химических соединений из простых веществ.

Реакция		Уравнение реакции	Коэффициент уравнения в линейной комбинации
r			Коэффициент уравнения в линейной комбинации
t	1		–1
	2		– 1
	3		+ 1

Если в линейную комбинацию входят реакции образования химических соединений из простых веществ, записанные относительно единственного продукта с единичным стехиометрическим коэффициентом, то для расчета стандартной мольной энтальпии какой-либо реакции

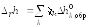
(7) где  стандартная мольная энтальпия образования вещества k (справочная величина, при 298 К).

(8)

При другой температуре:

Уравнение для расчета стандартного мольного изменения энтальпии в ходе химического превращения или уравнение Кирхгофа имеет вид

(9)

уравнение Кирхгофа

Разделяем переменные и интегрируем от 298 К до Т:

(10)

где – стандартная мольная теплота реакции образования вещества k.

Справочники содержат данные по при температуре 298 К и давлении 1 атм. Это позволяет рассчитать стандартную мольную теплоту любой реакции при этих условиях: