Расчет усилий и удельных давлений при осадке цилиндра

Р ассматривается осесимметричная пластическая деформация цилиндра между плоскими параллельными шероховатыми плитами.

При выводе приближенных уравнений равновесия для осесимметричной задачи в цилиндрических координатах R, , Z поместим начало координат в центре цилиндра.

Замечая, что при изменении Z от 0 до h/2 касательные напряжения _rz изменяются от 0 до значения  на контактных плоскостях, допустим, что напряжения _r и _ не зависят от Z.

Тогда, интегрируя одно из уравнений равновесия для осесимметричной задачи в цилиндрических координатах

(1.11)

в пределах от 0 до h/2, имеем

Производя необходимые преобразования, имеем следующее приближенное уравнение равновесия в цилиндрических координатах для осесимметричных задач

(1.12)

Это уравнение можно получить непосредственно из уравнения (1.11), если допустить линейное распределение касательных напряжений по координате Z, т.е. положить

, (1.13)

подставить это выражение в уравнение (1.11) и перейти от частных производных к обыкновенным.

Необходимо учитывать, что относительно нормальных напряжений на контактных плоскостях, через которые передается деформирующее усилие, уравнение (1.12), как и ранее полученное уравнение (1.3), по существу являются не приближенными, а лишь ограниченными, поскольку они выполняются лишь на контактной плоскости, т.е. при постоянном значении одной из координат.

Распространение этих уравнений на области деформируемого металла, лежащие вне контактных плоскостей, естественно приводит к получению неточных результатов, погрешность которых тем больше, чем меньше отношение .

Для нахождения компонентов напряжений на контактных плоскостях, воспользуемся приближенным уравнением равновесия (1.12).

Однако это уравнение содержит три компонента нормальных напряжений, следовательно статически неопределимо. Для решения необходимо наложить еще одно дополнительное условие на соотношение нормальных напряжений _r - _ .

Рассматривая осадку цилиндра на некоторую бесконечно малую величину dh, можно видеть, что компонентами деформации будут: осевая , радиальная , окружная .

Можно положить, что для любого радиуса _ = _r . Отсюда следует _r = _.

Следовательно, уравнение (1.12) приводится к виду:

(1.14)

Уравнение равновесия (1.14) решаем совместно с условием пластичности

(1.15)

Интегрируя уравнение (1.14) и определяя постоянные интегрирования для первого участка из граничного условия, что при ( т.е. на границе контактной плоскости ) , а для второго и третьего участка из условия непрерывности касательного напряжения на контактной плоскости для трех участков контактной плоскости, имеем в:

зоне скольжения для

(1.16)

зоне торможения для

(1.17)

зоне застоя для ; ( r_c h )

, (1.18)

г де .

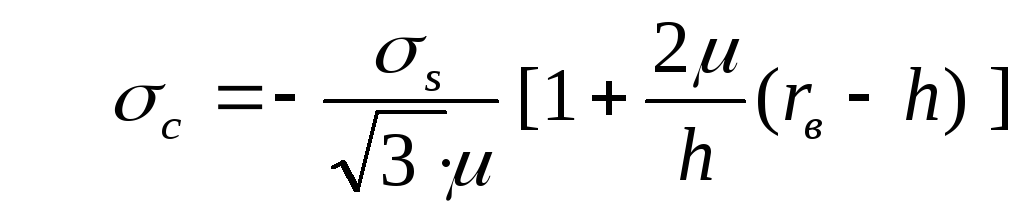Координата точки b, соответствующая границе зон скольжения и торможения, определяется исходя из условий, что в этой точке касательные напряжения достигают своего максимального значения, равного .

Решая уравнение с подстановкой вместо _z его значения из (1.16) относительно r=r_в имеем

(1.19)

Здесь

Как видно из последних выражений в условиях осадки осесимметричной поковки при , т.е. граница области торможения совпадает с границей контактной поверхности (плоскости), иначе говоря, область скольжения отсутствует.

В зависимости от соотношения возможны следующие виды эпюр нормальных и касательных напряжений:

1.Если ,

то эпюры кривых нормальных и касательных напряжений состоят из трех участков, определяемых выражениями (1.16) – (1.18).

Полное усилие осадки определяется как объем тела, ограниченного поверхностью пространственной эпюры нормальных напряжений и контактной плоскостью.

(1.20)

Под интегралами правой части соответственно подставляется _z из формул (1.16) – (1.18).

Среднее удельное давление, очевидно, равно частному от деления полного усилия на контактную площадь.

Выполняя интегрирование выражения (1.20) по соответствующим участкам и деля на площадь контакта, находим

(1.21)

Здесь d_в = 2r_в определяется из выражения (1.19), а r_c – радиус зоны застоя (прилипания), приближенно r_c h.

В частном случае, при =0,58 зона скольжения отсутствует, d_в = d и касательные напряжения на всей контактной плоскости (за исключением зоны застоя, где происходит их падение) будут постоянны и максимальны.

Для этого случая формула (1.21.) может быть упрощена и принимает вид

(1.22)

2.Если ,

то касательные напряжения на контактной плоскости ни в одной точке не достигают максимального значения и эпюра касательных напряжений определяется выражениями (поскольку точки b и с совпадают):

в зоне скольжения при

(1.23)

в зоне застоя при

, (1.24)

где

Удельное давление осадки для этого случая равно

(1.25)

3.Если ,

то кривые нормальных и касательных напряжений определяются выражением

(1.26)

Производя вычисление интеграла напряжений по контактной площади, находим для удельного давления осадки следующее выражение

(1.27)